37. Следствия из центральной предельной теоремы.

1. Распределение среднего арифметического

Пусть выполняются условия центральной предельной теоремы и . Тогда при

2. Нормальное приближение для

Пусть . При

3. Нормальное приближение для

Пусть при

38. Предмет и основные понятия математической статистики. Первичная обработка.

Математическая статистика – это наука о методах обработки результатов измерений с целью изучения случайных явлений.

Опр. Совокупность результатов измерений (1) случайной величины называют выборкой объема из генеральной совокупности

1. Основная задача математической статистики по выборке (1), максимально используя содержащуюся в ней информацию, сделать определенное заключение о генеральной совокупности .

2. Выборку (1) можно рассматривать:

1. Апостериорно (после измерений). Тогда (1) – это конкретных чисел

2. Априорно (до измерений). Тогда – это случайные величины с тем же законом распределения, что и .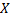

39. Первичная обработка выборки.

1. Вариационный ряд – это выборка упорядоченная в порядке неубывания

2. Эмпирическая (выборочная) функция распределения.

Пусть – число элементов выборки , удовлетворяющих неравенству

3. Разобьём отрезок на промежутки , точками деления .

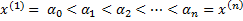Найдем попадание выборки значений в промежуток и отношение частоты . Составим таблицу:

			…
			…

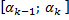
Она называется статистическим рядом.

4. Гистограмма – графическое изображение статистического ряда, т.е. ступенчатая фигура, состоящая из прямоугольников с основаниями и высотами , где – длина

Обозначим через функцию, графиком которой является огибающая. Результаты первичной обработки дают приблизительный закон распределения генеральной совокупности

Теорема Гливенко

При (т.е. является приближением к функции распределения генеральной совокупности )

Рассмотрим испытания по схеме Бернулли: если выборочное , то успех (всего n испытаний).

Тогда , где По теореме Бернулли

при (доказательство аналогично)

Пусть генеральная совокупность X – относится к непрерывному типу. Тогда при и max , где – функция плотности распределения.

40. Точечные оценки параметров распределения.

Опр. Правило (функция) с помощью которого по выборке находится приближенное значение параметра называется точечной оценкой этого параметра.

Замечания:

1. При априорном рассмотрении – случайной величины также является случайной величиной.

2. Оценку считают «хорошей», если она обладает свойствами:

1. Несмещенность

2. Состоятельность

3. (желательно) эффективность

Опр. Оценка параметра называется несмещенной, если . Если , то называется асимптотически несмещенной

Замечание: Несмещенность означает точность оценки «в среднем» отсутствие систематической ошибки.

Опр. Оценка параметра называется состоятельной если или . Состоятельность означает возможность за счет увеличения выборки получить любую требуемую точность.

Опр. Несмещенная оценка параметра называется эффективной если её дисперсия минимальна по сравнению со всеми возможными несмещенными оценками параметра

41 Несмещенность выборочного среднего и дисперсии (m неизвестно)

Оценки и являются несмещенными оценками m и

– несмещенная оценка m

– несмещенная оценка

42 Несмещенность выборочной дисперсии (m неизвестно)

Оценка является асимптотически несмещенной.

Отсюда

Но – асимптотически несмещена

– несмещенная оценка.

43. Состоятельность основных оценок параметров распределения (доказательство – для выборочного среднего).

являются состоятельными оценками соответствующих параметров.

Докажем для .

Применим второе неравенство Чебышева к при

44. Эффективность точечной оценки.

Опр. Несмещенная оценка параметра называется эффективной, если её дисперсия минимальна по сравнению со всеми возможными оценками

Замечания:

1. В отличие от несмещенности и состоятельности, эффективность зависит от закона распределения

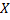
2. Для проверки эффективности можно использовать неравенство Крамера-Рао: , где ) – информация Фишера

Если выполняется, как равенство, то данная – эффективна.

45. Метод максимального правдоподобия.

Пусть снова . Требуется оценить векторный параметр .

Выборочный вектор – вектор (Х₁,Х₂…Х_n), где Х_i одинаково распределены и независимы (х₁,х₂…х_n) – реализация выборочного вектора.

Функция правдоподобия выборки:

- для непрерывного генерального – плотность распределения выборочного вектора, взятая в точке его реализации;

- для дискретного генерального – вероятность реализации данного выборочного вектора.

Обозначение

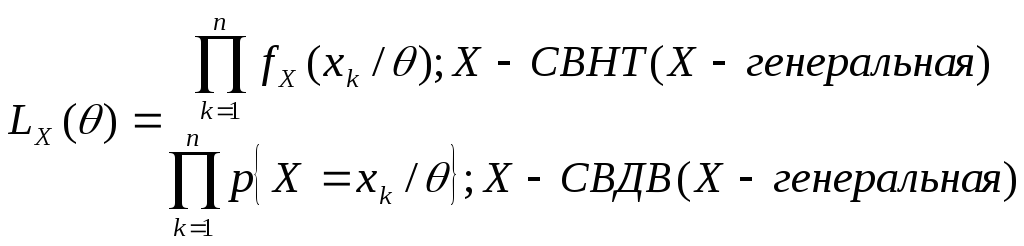
Оценками максимального правдоподобия (ММП-оценками) называются такие значения параметров (), которые доставляют максимум функции правдоподобия выборки.

Обозначим ММП-оценку вектора через . Пусть - внутренняя точка некоторого компакта S, функция L_x() дифференцируема в S. Тогда необходимым условием экстремума является равенство нулю всех производных первого порядка. Удобнее рассматривать экстремум не самой функции, а ее логарифма.