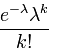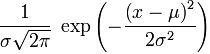- •12 Случайные велечины
- •16 Непр. Случайная. Величина.
- •37. Следствия из центральной предельной теоремы.
- •38. Предмет и основные понятия математической статистики. Первичная обработка.
- •39. Первичная обработка выборки.
- •40. Точечные оценки параметров распределения.
- •46. Метод моментов.
- •49.Распределение отношения выборочных дисперсий 2 норм генер совокупностей.
- •50. Интервальные оценки. Доверительный интервал. Доверительная вероятность.
- •51. Доверительный интервал для оценки мо при нЕизвестной дисперсии
- •51. Доверительный интервал для оценки мо при известной дисперсии
- •52.Доверительный интервал для оценки дисперсии при неизвестном мо.
- •53 . Проверка статистических гипотез
- •54 . Ошибки 1 и 2 рода
- •55. Критерий и его применение.
№1 Предмет теории вероятностей. Статистическая вероятность.
Предмет теории вероятностей.
Используется 2 основных типа моделей:
1)Детерминированная: При повторении заданного опыта в неизменных условиях, событие А происходит всякий раз.
П1. Опыт: К проводнику сопротивлением R приложено напряжение U. А={течет ток I=U/R}.
2) Вероятностная: При повторении опыта в неизменных условиях событие А может произойти или нет. Такие события и опыт называют случайными.
П2. Подбрасывают монету. A={Выпадет «герб»}.
ТВ изучает случайные события и их числовые характеристики.
Статистическая вероятность.
Еще в древности заметили статистическую устойчивость случайных явлений: если случайный опыт повторяется многократно, то отношение числа mn(A) появлений события А к числу n опытов приближается к некоторому числу P*(A). mn(A)/n= P*(A), n – велико.
P*(A) – статистическая вероятность. Используется при составлении частотных словарей, разработке клавиатуры и т.д.
№2 Случайные события и связанные с ними понятия. Алгебраические операции над событиями.
Случайные события.
Случайный опыт – это создание заданного комплекса условий и наблюдение результата. Результат интерпретируется как случайное событие(исход).
Пространство элементарных исходов
– мн-во простейших(неразложимых в рамках
данного опыта на более простые)
взаимоисключающих исходов
![]() так, что опыт всегда заканчивается
появлением одного и только одного
элементарного исхода
так, что опыт всегда заканчивается
появлением одного и только одного
элементарного исхода
![]() .
.
Случайное событие – любое подмн-во
![]() пр-ва элем. исходов заданного случайного
опыта. Если результат опыта
пр-ва элем. исходов заданного случайного
опыта. Если результат опыта
![]() ,
то событие А произошло.
,
то событие А произошло.
Основные понятия связанные со случайными событиями:
-
Всё пр-во элементарных исходов в
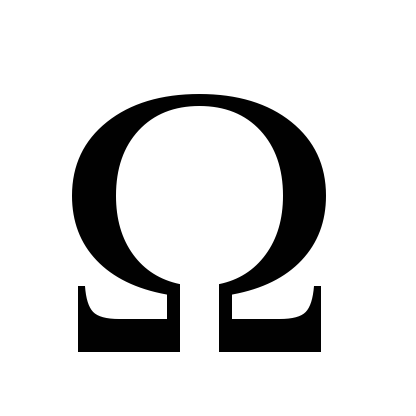 называется достоверным событием.
Очевидно достоверное событие происходит
в любом опыте.
называется достоверным событием.
Очевидно достоверное событие происходит
в любом опыте. -
Пустое множество Ǿ
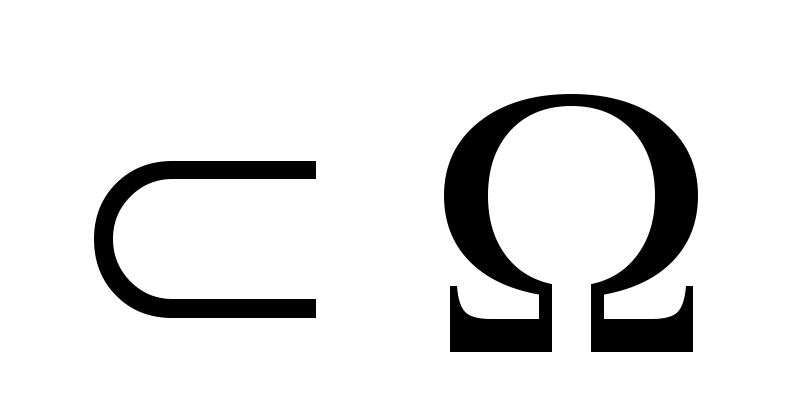 называется
невозможным событием. Очевидно
невозможное событие не происходит в
опыте.
называется
невозможным событием. Очевидно
невозможное событие не происходит в
опыте. -
Суммой событий А и В называется событие А+В состоящее из элем исходов входящих в мн-во
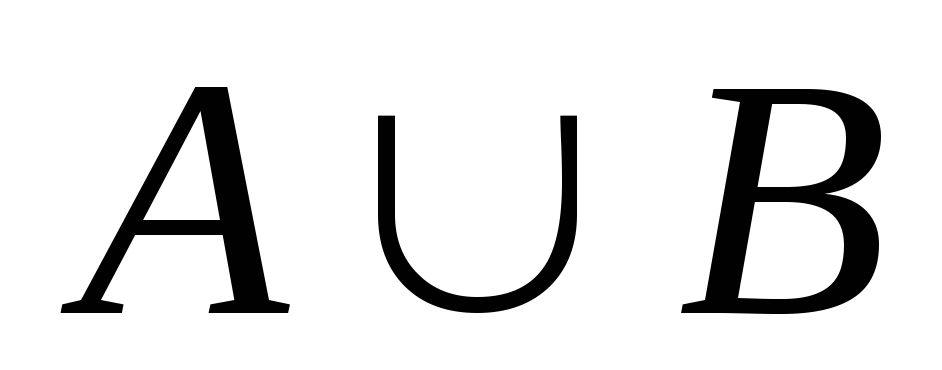 .
Т.о. событие А+В состоит в том что
произошло хотябы одно из событий А и
В.
.
Т.о. событие А+В состоит в том что
произошло хотябы одно из событий А и
В. -
Произведение А и В это событие сост. из элементарных исходов входящих в мн-во
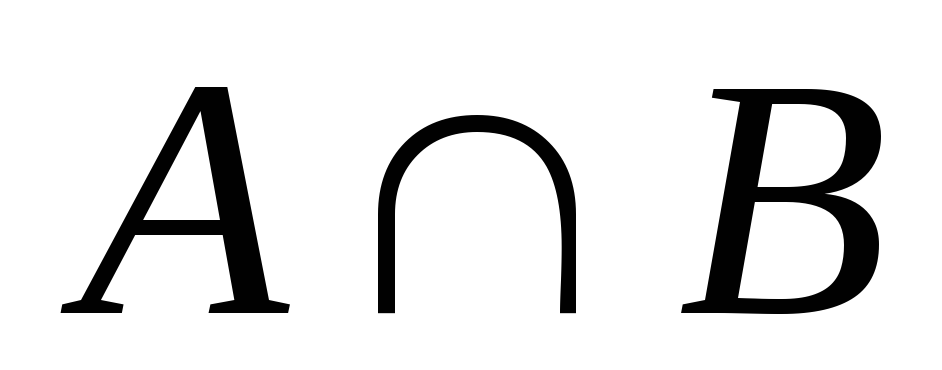 .
Т.о. произведение А и В состоит в том
что А и В произошли одновременно.
.
Т.о. произведение А и В состоит в том
что А и В произошли одновременно. -
Разность событий А и В – событие состоящее из элементарных исходов, входящих в мн-во А\В. Т.о. событие А произошло, а В нет.
-
Событие А влечет за собой В, если А – подмножество В(
 ).
Т.о. всякий раз, когда происходит А,
происходит и В.
).
Т.о. всякий раз, когда происходит А,
происходит и В.
-
Событие
 состоит из
состоит из
 ,
не входящих в А, называется противоположным
А
,
не входящих в А, называется противоположным
А -
События А и В называются несовместными если нет
 входяих в А и в В одновременно.
входяих в А и в В одновременно.
Св-ва:
1)Коммутативность:
А+В=В+А; АВ=ВА.
2)Ассоциативность:
(А+В)+С=А+(В+С); (АВ)С=А(ВС).
3)Дистрибутивность:
(А+В)С=АС+ВС; А+ВС=(А+В)(А+С).
№3 Классическое определение вероятности.
События равновероятные, если нет объективных оснований для того, чтобы, одно из них было более или менее вероятным чем другое.
Случайный опыт удовлетворяющий условиям:
а)
![]() конечно.
конечно.
б) все элем. исходы равновозможны
называется классической схемой.
Пусть
![]() классическая схема,
классическая схема,
![]() -число
элементарных исходов,
-число
элементарных исходов,
![]() -
число исходов благоприятствующих
событию А. Тогда вероятность события
А:
-
число исходов благоприятствующих
событию А. Тогда вероятность события
А:
Р(А)=
![]() /
/![]() - формула классической вероятности.
- формула классической вероятности.
Св-ва:
1)Р(А)>0
2)
![]()
3)Если А и В несовместны, (АВ= Ǿ), то Р(А+В)=Р(А)+Р(В).
№4 Геометрические вероятности
Пусть случайный опыт состоит в случайном выборе точки на прямой R1 или плоскости R2 или n мерного пространства Rn.
На прямой рассмотрим только мн-ва
![]() имеющие длину, на плоскости площадь, в
R3-объем, в Rn-
обобщенный объем.
имеющие длину, на плоскости площадь, в
R3-объем, в Rn-
обобщенный объем.
Длина, площадь, объем – мера множества
![]() .
.
Пусть случайная точка
![]() пропорциональна мере А (mes
A) и не зависит от других
обстоятельств. Такой случайный опыт
называется геометрической схемой.
пропорциональна мере А (mes
A) и не зависит от других
обстоятельств. Такой случайный опыт
называется геометрической схемой.
Пусть
![]() геометрическая схема, событие
геометрическая схема, событие
![]() -измеримое
мн-во. Тогда вероятностью события А
называется число P(A)=mes(A)/mes(
-измеримое
мн-во. Тогда вероятностью события А
называется число P(A)=mes(A)/mes(![]() )
)
П1. 2 судна должны подойти к причалу для разгрузки в течении суток. Одновременная разгрузка невозможна. Разгрузка любого из них длится 8 часов. С какиой вероятностью одно будет ожидать разгрузки другого?
х- время прихода однеого
у
y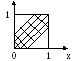 – время прихода другого
– время прихода другого
(х,у)
![]() в R2
в R2
![]() ={(х,у)
={(х,у)
![]() |
|
![]() }
}
A = {(х,у)
![]() |
|x-y|
|
|x-y|![]() 1/3}
1/3}
mes(![]() )=1,
mes(A)=5/9;
)=1,
mes(A)=5/9;
P(A)=5/9
Cв-ва:
1)Р(А)
![]()
2)
![]()
3)А и В несовместимы.
№5 Понятие об аксиоматической вероятности
Пусть
![]() событию
А, связанному со случайным опытом
событию
А, связанному со случайным опытом
![]() сопоставлена P(A).
Это означает, что на мн-ве всех событий
F определена числовая
функция P(A),
сопоставлена P(A).
Это означает, что на мн-ве всех событий
F определена числовая
функция P(A),
![]() .
.
Чтобы вместе с вероятностью событий А
и
![]() можно было найти А+В, АВ, А-В,
можно было найти А+В, АВ, А-В,
![]() ,
,
![]() ,
,
![]() ,
Ǿ, нужно чтобы эти события входили в F,
т.е. чтобы F было алгеброй
событий.
,
Ǿ, нужно чтобы эти события входили в F,
т.е. чтобы F было алгеброй
событий.
Если
![]() конечное или счетное мн-во, то алгеброй
событий F будет мн-во всех
подмн-в в
конечное или счетное мн-во, то алгеброй
событий F будет мн-во всех
подмн-в в
![]() .
.
П1. А={ из 4х карточек 1,2,3 и 4 случайно выбирают одну}
Найдем F:
Ǿ
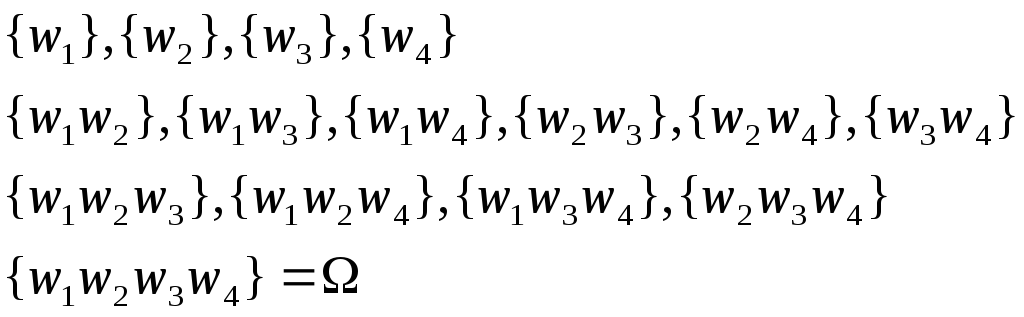
Пусть
![]() -
множество элем. исходов, F
– алгебра событий. Числова функция
Р(А), определенная на F,
называется вероятностью, если она
подчиняется аксиомам:
-
множество элем. исходов, F
– алгебра событий. Числова функция
Р(А), определенная на F,
называется вероятностью, если она
подчиняется аксиомам:
-
Р(А)
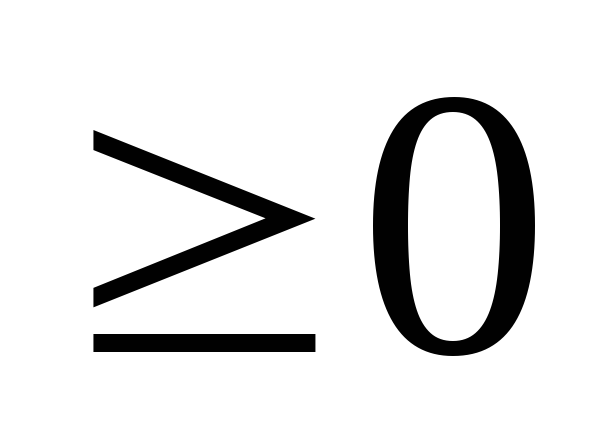 ,
,
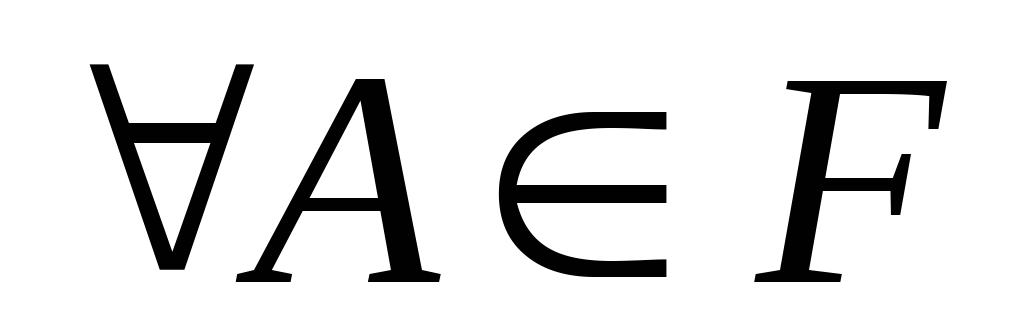 (аксиома
неотрицательности)
(аксиома
неотрицательности) -
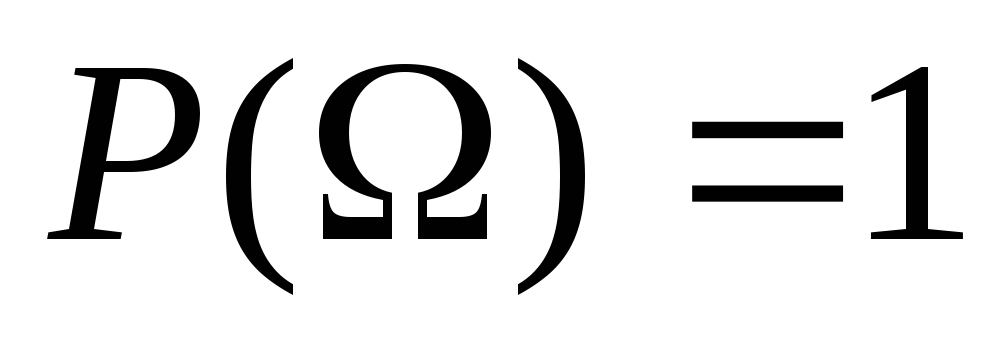 (аксиома нормировки)
(аксиома нормировки) -
Для
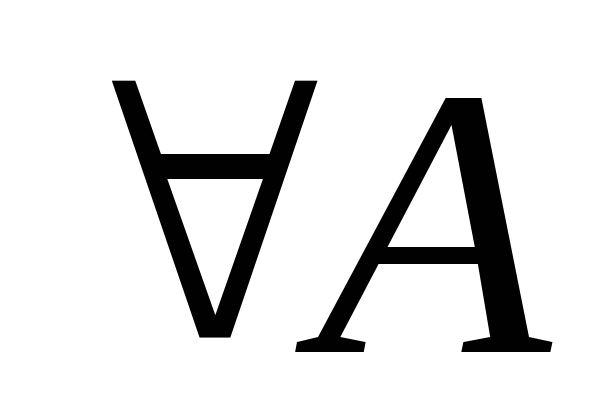 и В
и В
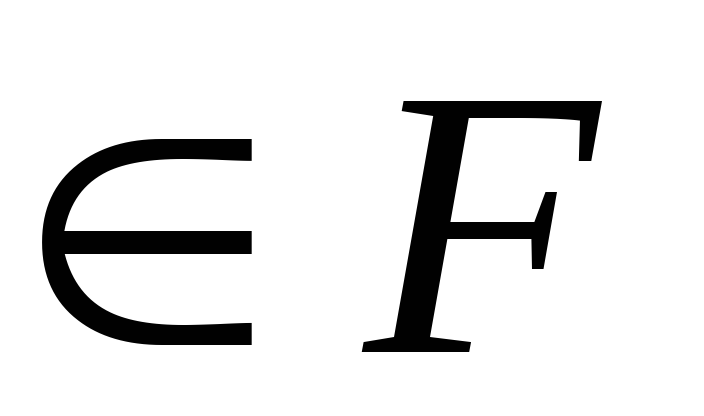 ,
таких что АВ= Ǿ. Р(А+В)=Р(А)+Р(В) (аксиома
сложения)
,
таких что АВ= Ǿ. Р(А+В)=Р(А)+Р(В) (аксиома
сложения)
1)![]()
2)![]() -
вероятность элементарного исхода
-
вероятность элементарного исхода
В П1 Р
![]()
№6 Св-ва вероятности
Из основных св-в вероятности:
1) Р(А)
![]()
2)![]()
3)АВ= Ǿ => Р(А+В)=Р(А)+Р(В)
Вытекают другие св-ва:
4)
![]()
5) Р(Ǿ)=0
6)
![]()
7)
![]()
8)Р(А+В)=Р(А)+Р(В)-Р(АВ)
№7 Условная вероятность и ее свойства. Теорема умножения.
Пусть в случайном опыте Т могут появиться события А и В. Если известно что В произошло то говорят об условной вероятности события А при условии В Р(А/В).
В произошло => реализуется один из
N(B) элементарных
исходов
![]() .
Из N(AB) исходов
.
Из N(AB) исходов
![]() благоприятствуют A
благоприятствуют A
![]()
Опр. Пусть (![]() ,F,P)
– вер. пространства , А,
,F,P)
– вер. пространства , А,
![]() и
и
![]() ,
тогда усл.вероятностью А наз-тся число
:
,
тогда усл.вероятностью А наз-тся число
:
![]()
Замеч. 1)Аналогично , если
![]() :
:
![]()
2) Теорема умножения Вер-ть
произведения
![]() событий равна вер-ти одного из них и
умноженной на усл.вер-ть другой.
событий равна вер-ти одного из них и
умноженной на усл.вер-ть другой.
1.
![]()
2.
![]()
3.
![]()
![]()
4)Усл вер-ть обладает всеми св-ми дрю вер-тей.
5) Усл. Вер-ть P(A/B)
можно рассм.,как обычную вероятность,
определенную на новом про-ве Эл. Исходов
![]()
6) Для n событий формула :
![]() обобщаеться
обобщаеться
![]()
№8 Независимые события, их свойства. Независимость в совокупности.
Опр. А независимое событие от В , если P(A/B)=P(A)
Свойства:
-
Свойство независимости взаимно, т.е. P(B/A)=P(B)
![]()
Т.е. А и В взаимно независимы.
2) Если А и В независимы , то P(AB)=P(A)*P(B) верно и обратное:
Опр. События А1,A2,A3,…,An независимы в совокупности , если любое из них не зависит от каждого из остальных n от всех возможных произведений этих остальных.
Опр. События A1,A2,…,An независимы в совокупности если : P(A1,A2,…,An)=P(A1)*P(A2)…P(An)
Замечание Для независимости в совокупности недостаточно попарной независимости.
№9 Формула полной вероятности.
Пусть события H1,…,Hn
могут произойти в случайном опыте Т.
Эти события образуют полную группу
событий, если H1+H2+…+Hn=![]()
Если к тому же события {Hz}
попарно несовместимы (Hi,Hj
![]() 0,
i
0,
i![]() j),
то они образуют полную группу несовместимых
событий , т.е. в каждом опыте происходит
одно и только одно из этих событий.
j),
то они образуют полную группу несовместимых
событий , т.е. в каждом опыте происходит
одно и только одно из этих событий.
Теорема.
Пусть в случ опыте могут произойти
события А,H1,..,Hn,
причем {Hi} образуют полную
группу несовместимых событий , то
![]()
A=A*![]() =A(H1+…+Hn)=AH1+…+AHn
=A(H1+…+Hn)=AH1+…+AHn
P(A)=P(AH1)+P(AH2)+…+P(AHn)=> теоре. Умножения
P(A)=P(H1)P(A/H1)+…+P(Hn)P(A/Hn)
№10 Формула Байеса
Теорема В условиях предыдущей теоремы
P(Hk/A)=(P(Hk)P(A/Hk))/P(A)
По теореме умножения P(A)*P(Hk/A)=P(A*Hk)=P(Hk)P(A/Hk) /: P(A)
P(Hk/A)=(P(Hk)P(A/Hk)/P(A))
№11 Схема Бернулли
Повторные испытания – это проведение n раз одного и тогоже случ опыта или проведение одновременное n одинаковых опытов.
Схема Бернулли – это случ опыт состоящий в n повторных испытаниях, причем
-
z исхода (А-успех, (не)А – неудача)
-
испытания независимы , т.е. P(A) не зависит от исходов в др. испытыниях
-
p и q=1-p не изм от пыта к опыту
Найдем вер-ть pn,m появления ровно m раз успеха в серии из т испытаний.
В силу независимости испытаний вер-ть
каждого такого исхода равно
![]() Число таких элементарных исходов
Число таких элементарных исходов
![]() Потому :
Потому :
![]()
12 Случайные велечины
Случайная величина = это числовая переменная, принимающая свои значения в зависимости от исхода некоторого случайного опыта
Опр. Пусть (![]() ,F,P)
– вер. Пространство, соответствующее
случ опыту Т. Числовая функция X=X(w),
определенная на
,F,P)
– вер. Пространство, соответствующее
случ опыту Т. Числовая функция X=X(w),
определенная на
![]() наз-тся случ величиной для
наз-тся случ величиной для
![]() числа x вещественного (
числа x вещественного (![]() )
мн-во
)
мн-во
![]() x
= {
x
= {![]() }
принадлежит алгебре событий F.Полную
инф-ю о случ величине ч содержит ее закон
расп-я , позволяющий найти Верн-ть для
}
принадлежит алгебре событий F.Полную
инф-ю о случ величине ч содержит ее закон
расп-я , позволяющий найти Верн-ть для
![]() события
, связанного с x
события
, связанного с x
Опр. Функцией распределения (Вер-тей) случ величины x наз функция : Fx(x)=P{X<x}
Св-ва Fx(x)
1 P{a<=x<b}=Fx(b)-Fx(a)
Пусть есть события {x<b},{x<a},{a<=x<=b}
{x<b}={x<a}+{a<=x<=b}
![]()
![]()
2 P{a<=x<=b}=Fx(b+0)-Fx(a)
3 P{a<x<b}= Fx(b)-Fx(a+0)
4 P{a<x<=b}=Fx(b+0)-Fx(a)
5 P{x=a} = Fx(a+0)-Fx(a)
Другие свойства
1 Fx(x) не убыв функция
2 0<=Fx(x)<=1
3 Fx(-![]() )=0
, Fx(+
)=0
, Fx(+![]() )=1
)=1
4 Fx(x) в t
точках a![]() ГR
непр слева
ГR
непр слева
№13 Дискретная случайная величина
Опр Случайная величина X, мн-во значений которой конечно или счетно называеться случайной величиной дискретного типа (СВДТ)
Закон распределения СВДТ описываеться с помощью Fx, но удобнее представлять в виде ряда распределений
![]() Fx(x)=P{X<x}=
Fx(x)=P{X<x}=![]()
Очевидно что сумма =1
Св-ва Fx(x) СВДТ :
а) кусочно постоянная
б) Fx(x)=0 при x<x1
в) в точка xi терпит разрыв 1-го рода
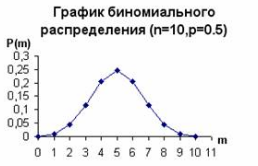
№14 Биноминальное распределение
Дискретная X имеет бин
распределение с параметрами n,
p(X~B(n,p)),
если X принимает 0,1,…,n
с Вер-мя p(n,k)=
P{X=k}=
![]()
Очевидно B(n,p) описывает случ число успехов в серии n испытаний по схеме Бернулли с вер-тью успеха p.
Опр. Пусть X-CВДТ
с рядом расп-й причем числовой ряд
![]() сх-ся , тогда m=M[x]=
сх-ся , тогда m=M[x]=
![]() наз-ся математическим ожиданием
(m-ср.знач.X)
наз-ся математическим ожиданием
(m-ср.знач.X)
Для бин распр-я:
X=![]() , где Xk 0 1
, где Xk 0 1
P q p
M[x]=
![]()
Дисперсия B(n,p):
D[X]=
![]()
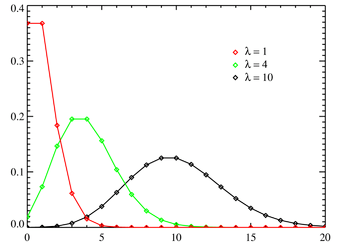
№15 Распределение Пуассона
Теорема Пуассона
Пусть n->бесконечность
и p->0 так что np=![]() =const
, тогда
=const
, тогда
![]()
![]() Случайная
величина X со знач 0,1,2,…,k
и вер-ми pk=p{X=k}=
Случайная
величина X со знач 0,1,2,…,k
и вер-ми pk=p{X=k}=
![]() ,
,
![]() >0
имеем распр-е Пуассона с пар
>0
имеем распр-е Пуассона с пар
![]() (X~Pn(
(X~Pn(![]() ))
))
З-и Pn(![]() )
описывает явления с большим числом
испытаний и малой вер-тью успеха (з-н
редких явлений)
)
описывает явления с большим числом
испытаний и малой вер-тью успеха (з-н
редких явлений)
Мат ожидание :
![]()
Дисперсия : Dx=![]()
16 Непр. Случайная. Величина.
Опр. X наз-ся непр,
если
![]() неотриц функция Fx(x)(функция
плотности расп-я), так что :
неотриц функция Fx(x)(функция
плотности расп-я), так что :
Fx(x)=P{X<x}=![]()
Св-ва fx(x) :
1 P{a<=X<b}=![]()
2 для любого a принадлежащего ГR P{X=a}=0
3 fx(x)>=0
4
![]() (условие нормировки
(условие нормировки
5 В точках непр-ти : fx(x)=F’x(x)
№17 Нормальный закон распределения
Непр случайная величина X
распределена по нормальному з-ну распр-я
с параметрами m,t(X~N(m,t))
если ее функция плотности имеет вид
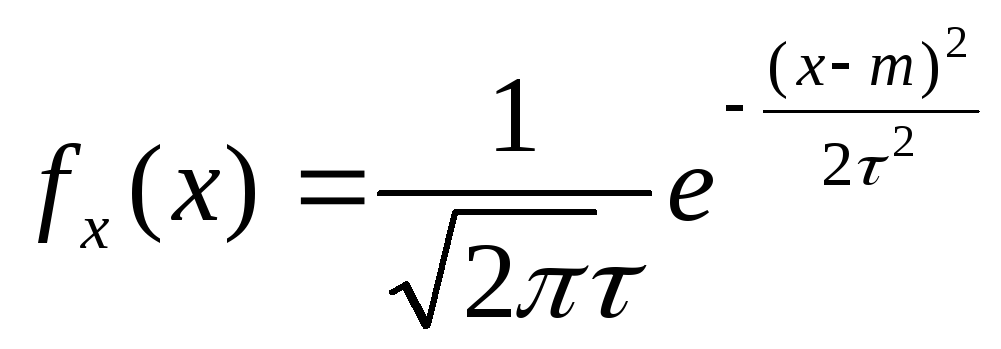
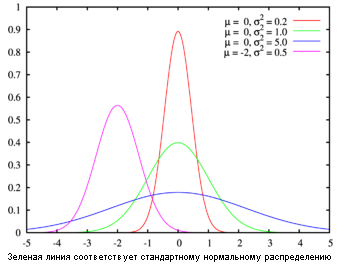
Распределение N(0,1) называеться стандартизированным нормальным :
Ф(x)=
![]() -функция
Лапласа
-функция
Лапласа
Благодаря св-ву Ф(-x)=(-Ф(x)), x>=0 в таблицу можно приводить значения Ф(x) только для x>=0
Математическое ожидание
M[x]=
![]() ->
M[x]=m
->
M[x]=m
Дисперсия
D[x]=
![]()
Найдем для x~N(m,
![]() )
P{a<x<b}
)
P{a<x<b}
P{a<x<b}=![]()
![]()
В частном случае P{/X-m/<l}=2Ф(l/![]() )-1
)-1
-
Случайный вектор. Функции совместного распределения вероятностей, её свойства.



-
Дискретный случайный вектор. Связь закона распределения двумерного случайного вектора с законами распределения его компонент. Независимость случайных величин. Условные законы распределения.




-
Математическое ожидание дискретной случайной величины, его свойства.

22. Начальные и центральные моменты
Опр. Начальным моментом k-ого порядка X называется число
αk[X]=M[X![]() ]
]
1) α1[X]=M[X]
2) X – СВДТ => αk[X]=∑
X![]() p
p
Опр. Центр. моментом k-ого порядка X называется число
μk[X]=M[(X-M[X])![]() ]
]
1) Сл.величина X-M[X]=X (с точкой сверху) наз-ся центрир. случ. величиной.
2) μ1[X]=0
Связь между αk[X] и μk[X].
μk=M[(X-M[X])![]() ]=
M[
]=
M[![]() X
X![]() (-1)
(-1)![]() (M[X])
(M[X])![]() ]=
]=
=![]()
![]() M[X
M[X![]() ](M[X])
](M[X])![]()
=> μk[X]
=
![]()
![]() αj[X]
* α
αj[X]
* α![]() [X]
[X]
23. Дисперсия случайной величины
Опр. Дисперсией случ.величины X назыв. ее второй центральный момент μ2[X]:
D[X] =
M[(X-M[X])![]() ]
]
Для X – СВДТ: D[X]
=
![]() pi
pi
D[X] характеризует степень рассеяния, разбросанности значений X вокруг M[X].
Опр. Среднеквадратическим отклонением
X назыв. число T[X]
=
![]()
Свойства:
1. D[X] больше, либо равно 0
2. D[C] = 0, C=const
3. D[X] = M[X![]() ]-M
]-M![]() [X]
[X]
4.D[cX] = c![]() D[X]
D[X]
5.Если X и Y независимы, то D[X+Y] = D[X]+D[Y]
D[X+Y] = M[(X+Y-M[X+Y])
![]() ]
= M[(X-M[X]+Y-M[Y])
]
= M[(X-M[X]+Y-M[Y])![]() ]
=
]
=
= M[(X-M[X])
![]() ]+M[(Y-M[Y])
]+M[(Y-M[Y])
![]() ]
+ 2M[(X-M[X])]*M[(Y-M[Y])] =
]
+ 2M[(X-M[X])]*M[(Y-M[Y])] =
= D[X] + D[Y] | M1=0 | | M1=0 |
24. Мат.ожидание и дисперсия СВНТ
Опр. Пусть X – СВНТ с
функцией плотности fx(x),
причем
![]() fx(x)dx
сходится абсолютно, тогда мат. Ожиданием
X называется число M[X]
=
fx(x)dx
сходится абсолютно, тогда мат. Ожиданием
X называется число M[X]
=
![]() fx(x)dx
fx(x)dx
Опр. Пусть X – СВНТ с
функцией плотности fx(x),
причем
![]() fx(x)dx
сходится абсолютно, тогда дисперсией
X называется число: D[X]
=
fx(x)dx
сходится абсолютно, тогда дисперсией
X называется число: D[X]
=![]() fx(x)dx
fx(x)dx
Замечание.
1)M[X] для X – СВНТ обладает теми же свойствами, что и для X-СВДТ
2)Опр-е нач. и центр. моментов сохр. на случай непр. случ. величины. Их свойства зависят от свойств M[X].
П1. X~N(m,τ);M[X] - ?
M[X] =
![]()
![]() dx=…=
m = M[X]
dx=…=
m = M[X]
П2. X~N(m,τ);D[X] - ?
D[X] = =
![]()
![]() dx=…
=
dx=…
=
![]()
25. Функция случайной величины.
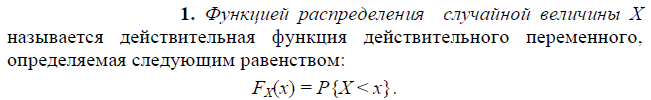




26. Характеристики распределения случайной величины: мода, медиана, квантили, коэффициенты асимметрии и эксцесса.
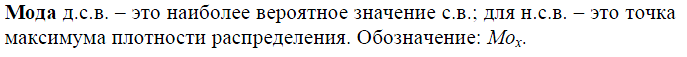



![]()
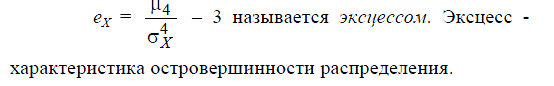
![]()
-
Характеристическая функция случайной величины, её свойства.



28. Характеристические функции биноминального, пуассоновского и нормального распределений вероятности.
Биномиальное распределение в теории вероятностей — распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна p.
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона играет ключевую роль в Теории массового обслуживания.
Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний
№29 Композиционая устойчивость
Опр.: Пусть X1 и Х2 распределены по одному и тому же закону (возможно с разными параметрами) и независимы. Если при этом Х1+Х2 распределена по тому же закону, то говорят, что данный закон композиционно устойчив.
П1: ![]() ,
, ![]() и Х1,Х2 независимы
и Х1,Х2 независимы
• ![]() ,
, ![]() . Т.к. Х1 и Х2 независимы:
. Т.к. Х1 и Х2 независимы: ![]() =>
=> ![]() •
•
Т.е. при фиксированном значении p з-н B(n,p) композиционно устойчив.
П2: ![]() ,
, ![]()
• ![]() ,
, ![]() .
Т.к. Х1 и Х2 независимы:
.
Т.к. Х1 и Х2 независимы: ![]() =>
=> ![]() •
•
П3: ![]() ,
, ![]() и Х1,Х2 независимы
и Х1,Х2 независимы
• ![]() ,
, ![]()
![]() =>
=> ![]() •
•
№30 Ковариация двух случайных величин:
Опр: Ковариацией Х и Y
называется число (если ![]() ):
):
сov[X,Y] = M[(X-M[X])(Y-M[Y])]= M[Ẋ,Ẏ].
Св-ва:
-
сov[X,Y] = сov[Y,X]
-
сov[X,X] = D[X]
-
сov[X,Y1+Y2] = сov[X,Y1] + сov[X,Y2]
-
сov[C*X,Y]= C* сov[X,Y]
-
D[X+Y]=D[X] + D[Y] + 2 сov[X,Y]
-
|сov[X,Y]| ≤
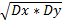
• 0≤ D[tX+Y] = t^2*D[X] + D[Y] + 2t*cov[X,Y]
![]() = 4 (сov[X,Y])^2
– 4* D[X]*D[Y] => |сov[X,Y]|
≤
= 4 (сov[X,Y])^2
– 4* D[X]*D[Y] => |сov[X,Y]|
≤ ![]() •
•
№31 Коэффициент корреляциии.
Опр: Коэффициентом корреляции называется число:
![]()
Св-ва:
-
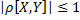
-
Если X и Y независимы =>
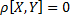 (обратное неверно)
(обратное неверно)
•cov[X,Y]=M[XY]
– M[X]M[Y]
= |тк Х и Y
независимы|= M[X]M[Y]
– M[X]M[Y]
=0 =>![]() •
•
-
Если Y=aX+b, то

• Пусть
M[X]
= m
, D[X]=![]() тогда M[Y]
= am+b
, D[Y]=
тогда M[Y]
= am+b
, D[Y]=![]()
cov[X,Y]
= M[(X-m)(ax+b – (am+b))] = a* M[(X-m)^2] = ![]()
![]() •
•
Замеч: Если X и Y
независимы, то ![]() .
Если Х и Y лин. зависимы
.
Если Х и Y лин. зависимы
![]() .
Поэтому
.
Поэтому ![]() используется в качестве меры линейной
зависимости Х и Y. Если
используется в качестве меры линейной
зависимости Х и Y. Если
![]() – зависимость слабая. Если
– зависимость слабая. Если ![]() - зависимость сильная. Если
- зависимость сильная. Если ![]() - то при росте одной случайной величины,
другая в среднем растет.
- то при росте одной случайной величины,
другая в среднем растет.
№32 Распределения ![]()
Опр: Пусть Xi –
независимые случайные величины, ![]() .
Тогда случайная величина
.
Тогда случайная величина ![]() имеет распределение
имеет распределение ![]() (
«хи-квадрат») с n степенями
свободы -
(
«хи-квадрат») с n степенями
свободы - ![]()
Св-ва:
-
M[Y]=n ; D[Y]=2n
-
Рисуем графики (оси: f
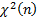 (x)
и ось «х»)...n2>n1
хотя n2
более пологий и лежит ниже n1
(x)
и ось «х»)...n2>n1
хотя n2
более пологий и лежит ниже n1
Опр: Пусть случ. величины ![]() и
и ![]() независимы. Тогда случ. величина Y
распределена по закону Стьюдента:
независимы. Тогда случ. величина Y
распределена по закону Стьюдента: ![]() с n степенями свободы.
с n степенями свободы.
![]() .
.
-
Рисуем графики (оси: St
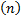 (x)
и ось «х»)...n1>n2
- n2
более пологий и лежит ниже n1
(x)
и ось «х»)...n1>n2
- n2
более пологий и лежит ниже n1 -
При
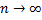 St(0,1)
приближается к N(0,1)
St(0,1)
приближается к N(0,1)
Опр: Пусть ![]() и
и ![]() - независимые случайные величины. Тогда
- независимые случайные величины. Тогда
![]() распределена по закону Фишера со
степенями свободы n1 и n2
распределена по закону Фишера со
степенями свободы n1 и n2
Св-во: Пусть Fn1,n2,p – квантиль распределения F(n1,n2) порядка p, тогда Fn1,n2,(1-p) = 1/ Fn1,n2,p
№33 Неравенства Чебышева
Теорема 1 ( 1ое неравенство Чебышева) :
Пусть Х – случайная величина, ![]() .
Тогда
.
Тогда ![]()
• Рассмотрим случайную величину ![]()
Очевидно, ![]() или
или ![]() ;
;
![]() •
•
Теорема 2 (2ое неравенство Чебышева):
Пусть Х-случайная величина, ![]() ,
,
![]() .
Тогда
.
Тогда ![]()
• Рассмотрим непр. Х:
![]() •
•
№34 Закон больших чисел(теорема
Маркова):
Опр: Говорят, что
последовательность случ. величин ![]() сходится по вероятности к числу a
(
сходится по вероятности к числу a
(![]() ),
если
),
если ![]() ( или
( или ![]() )
)
Теорема Маркова:
Пусть последовательность случ величин
![]() удовлетворяет условиям:
удовлетворяет условиям: ![]() и
и ![]() .
Тогда
.
Тогда ![]() ,
т.е.
,
т.е. ![]() .
.
•Обозначим ![]() ,
,
![]() ,
,
![]() .
Применяем второе неравенство Чебышева:
.
Применяем второе неравенство Чебышева:
![]() •
•
№35 Следствия из закона больших чисел
1) Теорема Чебышева
Пусть ![]() – последовательность независимых или
попарно некоррелированных случ.
величин(*).:
– последовательность независимых или
попарно некоррелированных случ.
величин(*).: ![]() и
и ![]() .
Тогда Тогда
.
Тогда Тогда ![]()
2)
Пусть ![]() - последовательность одинаково распр.
случ. величин, удовл. условию (*).
- последовательность одинаково распр.
случ. величин, удовл. условию (*).
![]() ,
,
![]() .
Тогда
.
Тогда ![]() или
или ![]()
3) Пусть ![]() ,
т.е
,
т.е ![]() - число успехов в серии n
испытаний в схеме Бернулли с вероятностью
успеха p. Тогда
- число успехов в серии n
испытаний в схеме Бернулли с вероятностью
успеха p. Тогда ![]() ,
т.е
,
т.е ![]()
•![]()
|
Xk |
0 |
1 |
|
p |
q |
p |
![]()
![]() по следствию (2)•
по следствию (2)•
№36 Центральная предельная теорема
Опр: Пусть ![]() - последовательность случайных величин.
Говорят, что случайная величина
- последовательность случайных величин.
Говорят, что случайная величина ![]() имеет асимптотическое нормальное
распределение с параметрами
имеет асимптотическое нормальное
распределение с параметрами ![]() при
при ![]() ,
если для
,
если для ![]()
![]() .
.
![]() - функция Лапласа. Обозн:
- функция Лапласа. Обозн: ![]() .
.
Теорема:
Пусть последовательность ![]() удовлетворяет условиям:
удовлетворяет условиям:
-
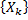 - независимы.
- независимы. -
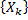 - одинаково
распределены
- одинаково
распределены -
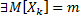 ,
,
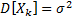
Тогда для ![]() справедливо
справедливо ![]() .
.
Замечания:
1)При достаточно больших n
- ![]() ,
т.е. сумма большого числа одинаково
распределенных независимых случайных
величин имеет распределение, близкое
к нормальному.
,
т.е. сумма большого числа одинаково
распределенных независимых случайных
величин имеет распределение, близкое
к нормальному.
2) Условие (2) не является принципиальным.
Если ![]() ,
, ![]() ,
то при некоторых требованиях вместо
условия (3) при больших n
имеем:
,
то при некоторых требованиях вместо
условия (3) при больших n
имеем:
![]() ,т.е. и в этом случае сумма достаточно
большого числа случайных величин
распределена приблизительно нормально.
,т.е. и в этом случае сумма достаточно
большого числа случайных величин
распределена приблизительно нормально.