Расчет резервов времени
Резерв времени события R определяется как разность между поздним и ранним сроками наступления события и показывает, на какое предельно допустимое время можно задержать наступление этого события. Не увеличивая общего срока окончания всех работ Rj = Tн j – Тр j.
Очевидно, что для любой работы, лежащей на критическом пути,
R н i-j=0.
Состав критического пути
Рассчитаем длины полных путей сетевой модели. Для этого разобьем сеть на элементарные пути.
Т(L11{0, 2,1, 4, 6, 7}) = 1+1+2+3+1=7
Т(L12{0, 1, 5, 3,7 }) = 1+4+2+1=8
Т(L21{7, 8, 9, 10, 11, 12,13}) = 1+2+1+1+1+7=13
L1=T(L11) + T(L21) = 6+13 = 20
L2=T(L12) + T(L21) = 8+13 = 21=> Lкр
Определим вершины принадлежащие критическому пути, устанавливающиеся из условия Tн j – Тр j = 0. Таким образом, критический путь состоит из вершин:
LКР = {0, 1, 3, 5, 7, 8, 9, 10, 11, 12, 13}.
Полученные основные временные параметры сведем в табл. 3 и 4.
Таблица 3.
ООсновные временные параметры сетевой модели
|
№ п/п |
Код работы |
Топт |
Трн |
Тро |
Тпн |
Тпо |
|
1 |
0-1 |
1 |
0 |
5 |
2 |
7 |
|
2 |
1-4 |
1 |
5 |
8 |
7 |
10 |
|
3 |
1-5 |
2 |
5 |
17 |
7 |
19 |
|
4 |
2-6 |
2 |
8 |
13 |
10 |
15 |
|
5 |
3-7 |
5 |
17 |
19 |
19 |
21 |
|
6 |
2-7 |
4 |
13 |
16 |
15 |
18 |
|
7 |
6-7 |
1 |
19 |
21 |
21 |
23 |
|
8 |
7-8 |
1 |
19 |
23 |
21 |
25 |
|
9 |
8-9 |
2 |
19 |
24 |
21 |
26 |
|
10 |
9-10 |
1 |
16 |
19 |
18 |
21 |
|
11 |
10-12 |
1 |
23 |
28 |
25 |
30 |
|
12 |
12-13 |
6 |
24 |
29 |
26 |
31 |
Таблица 2.
Таблица 4.
Основные временные параметры сетевой модели (по кодам событий)
|
Номер события |
ТРi |
ТПi |
Ri |
|
0 |
0 |
0 |
1 |
|
1 |
1 |
2 |
1 |
|
2 |
2 |
3 |
1 |
|
3 |
7 |
8 |
1 |
|
4 |
4 |
5 |
1 |
|
5 |
5 |
6 |
1 |
|
6 |
7 |
8 |
1 |
|
7 |
15 |
16 |
1 |
|
8 |
16 |
17 |
1 |
|
9 |
18 |
19 |
1 |
|
10 |
19 |
20 |
1 |
|
11 |
20 |
21 |
1 |
|
12 |
21 |
22 |
1 |
|
13 |
28 |
29 |
1 |
Оптимизация сетевого графика Оптимизация по временным параметрам
Вычислим коэффициент напряженности работы, позволяющий определить, насколько свободно можно располагать имеющимися резервами времени.
где
– совпадающая с длиной критического
пути величина отрезка пути, проходящего
через данную работу.
Представим данные в виде таблицы 5:
ОТаблица 5.
|
Код работы |
Rпi-j |
T(L’кр) |
Kнi-j |
|
1-2 |
1 |
19 |
0,97 |
|
2-4 |
3 |
19 |
0,91 |
|
4-6 |
3 |
19 |
0,91 |
|
5-7 |
10 |
22 |
0,66 |
|
5-8 |
1 |
29 |
0,95 |
|
6-10 |
4 |
19 |
0,88 |
|
8-11 |
2 |
29 |
0,91 |
Также, рассчитывается вероятность свершения события конечного в заданный срок, причем 0,35 < РК < 0,65.
Вероятность выполнения проекта к директивному сроку сводится к вычислению вероятности попадания в область кривой нормального распределения при заданном математическом ожидании и дисперсии некоторой случайной величины, представляющей длительность проекта.
Дисперсия (мера разброса ожидаемого времени выполнения) работ, лежащих на критическом пути, при двух экспертных оценках, равны:
Результаты расчета дисперсии представлены в таблице 6.
Таблица 6
|
Номер события |
ТРi |
ТПi |
2 |
|
0-1 |
1 |
2 |
0,04 |
|
1-5 |
7 |
8 |
0,04 |
|
3-7 |
5 |
6 |
0,04 |
|
6-7 |
15 |
16 |
0,04 |
|
7-8 |
16 |
17 |
0,04 |
|
8-9 |
18 |
19 |
0,04 |
|
9-10 |
19 |
20 |
0,04 |
|
10-12 |
20 |
21 |
0,04 |
|
12-13 |
21 |
22 |
0,04 |
|
|
|
|
Сумма: 0,36 |
Вероятность будет определяться значением функции нормального распределения с аргументом z, равным:
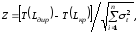
Z=(52-51) / 1,83 = 0,54
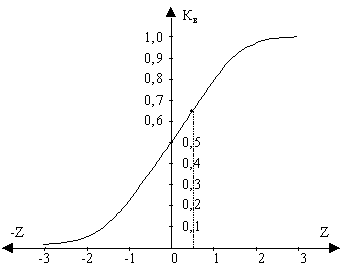
Рис. 6
Найдя Z по графику функции (рис. 6) нормального распределения, определим вероятность свершения завершающего события в заданный срок.
РК = f(Z) =0,64.
Можно сделать вывод, что рассматриваемая работа будет выполнена в заданный срок, т.к. 0,35 < Р < 0,65.