
- •1.1. Событие и эксперимент. Соотношения между событиями. Пространство элементарных исходов
- •1.2. Относительная частота и вероятность события. Статистическое определение вероятности
- •1.3. Классическое определение вероятности
- •1.5. Аксиоматика теории вероятностей
- •1.6. Условная вероятность. Независимость событий. Теорема умножения вероятностей
- •1.8. Формула полной вероятности
- •1.9. Формула Байеса
- •2.1. Понятие случайной величины. Дискретные и непрерывные величины
- •2.2. Ряд и многоугольник распределения дискретной св
- •2.3. Функция распределения св и её свойства
- •2.4. Плотность распределения непрерывной св и её свойства
- •2.5. Математическое ожидание, мода и медиана св
- •2.1. Понятие о точечных оценках и их свойствах
- •2.2. Точечные оценки математического ожидания, дисперсии и среднего квадратического отклонения
- •3.1. Понятие о доверительных интервалах
- •4.1. Основные определения и общая схема проверки гипотез
2.2. Ряд и многоугольник распределения дискретной св
Пусть Х – дискретная СВ, которая в
результате опыта принимает одно из
значений
![]() ,
а
,
а
![]() ,
,
![]() – вероятности появления этих значений.
События
– вероятности появления этих значений.
События
![]() ,
,
![]() являются, очевидно, попарно несовместными
и образуют полную группу, поэтому
являются, очевидно, попарно несовместными
и образуют полную группу, поэтому
 .
.
Законом распределения дискретной СВ
называется любое соотношение,
устанавливающее связь между её возможными
значениями
![]() и их вероятностями
и их вероятностями
![]() .
Простейшей формой задания закона
распределения дискретной СВ с конечным
множеством значений является следующая
таблица, называемая рядом распределения:
.
Простейшей формой задания закона
распределения дискретной СВ с конечным
множеством значений является следующая
таблица, называемая рядом распределения:
-
Х


. . .
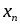
р


. . .

Предполагается, что
![]() .
Если множество возможных значений
.
Если множество возможных значений
![]() дискретной СВ счетное, то её ряд
распределения иногда удаётся представить
формулой вида
дискретной СВ счетное, то её ряд
распределения иногда удаётся представить
формулой вида
![]() ,
,
![]() ,
где р – некоторая функция и выполняется
условие
,
где р – некоторая функция и выполняется
условие
![]() .
.
2.3. Функция распределения св и её свойства
Пусть Х – некоторая СВ. Функция
![]() называется функцией распределения этой
СВ. Функция распределения может
использоваться в качестве вероятностной
характеристики как дискретной, так и
непрерывной СВ. Рассмотрим основные
свойства
называется функцией распределения этой
СВ. Функция распределения может
использоваться в качестве вероятностной
характеристики как дискретной, так и
непрерывной СВ. Рассмотрим основные
свойства
![]() .
.
1.
![]() .
2.
.
2.
![]() – неубывающая функция аргумента х.
3.
– неубывающая функция аргумента х.
3.
![]() .
4.
.
4.
![]() .
5.
.
5.
![]() .
.
6. Функция распределения непрерывной СВ непрерывна на всей числовой оси.
7. Функция распределения дискретной СВ является ступенчатой и непрерывной слева при любом значении аргумента х. Она имеет разрыв при каждом значении аргумента, совпадающем с возможным значением СВ, а величина соответствующего скачка равна его вероятности.
2.4. Плотность распределения непрерывной св и её свойства
Пусть Х – непрерывная СВ, а
![]() – её функция распределения, которая
предполагается дифференцируемой.
– её функция распределения, которая
предполагается дифференцируемой.
![]() Рассмотрим основные свойства плотности
распределения.
Рассмотрим основные свойства плотности
распределения.
1.
![]() .
2.
.
2.
![]() .
3.
.
3.
![]() .
4.
.
4.
![]() .
.
2.5. Математическое ожидание, мода и медиана св
Математическим ожиданием дискретной
СВ Х, которая может принимать значения
![]() ,
называется величина
,
называется величина
![]() ,
где
,
где
![]() ,
,
![]() и
и
![]() .
Если множество значений дискретной СВ
счётно, то
.
Если множество значений дискретной СВ
счётно, то
![]() .
.
Математическим ожиданием непрерывной
СВ Х с плотностью распределения
![]() называется величина
называется величина
![]() .
.
Модой Мо дискретной СВ называется
такое её возможное значение
![]() ,
для которого вероятность
,
для которого вероятность
![]() наибольшая. Модой непрерывной СВ
называется такое из её значений, которому
соответствует наибольшее значение
плотности вероятности
наибольшая. Модой непрерывной СВ
называется такое из её значений, которому
соответствует наибольшее значение
плотности вероятности
![]() .
.
Медианой Ме непрерывной СВ Х
называется такая величина, для которой
![]() .
Если известна функция распределения
.
Если известна функция распределения
![]() ,
то медиана определяется как корень
уравнения
,
то медиана определяется как корень
уравнения
![]() .
.
2.6. Моменты, дисперсия и среднее квадратическое отклонение СВ
Начальным моментом k-го порядка СВ Х
называется величина
![]() .
Для дискретной СВ
.
Для дискретной СВ
![]() ,
для непрерывной
,
для непрерывной
![]() .
.
![]() совпадает с математическим ожиданием.
Случайная величина
совпадает с математическим ожиданием.
Случайная величина
![]() называется центрированной по отношению
к СВ Х. Центральным моментом k-го порядка
СВ Х называется величина
называется центрированной по отношению
к СВ Х. Центральным моментом k-го порядка
СВ Х называется величина
![]() .
Центральный момент
.
Центральный момент
![]() всегда равен нулю. Центральный момент
всегда равен нулю. Центральный момент
![]() называется дисперсией СВ Х. Справедливо
равенство
называется дисперсией СВ Х. Справедливо
равенство
![]() .
.
4.3. Основные свойства математического ожидания
1. Если с – константа, то
![]() .
.
2. Если с – константа, Х – СВ, то
![]() .
.
3. Если Х и Y – две СВ, то
![]() .
.
по индукции можно получить равенство
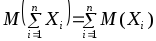 .
.
4. Если Х и Y – две СВ, то
![]() .
.
Если Х и Y не коррелированны, то
![]() .
Если
.
Если
![]() – независимые СВ, то
– независимые СВ, то
 .
.
4.4. Основные свойства дисперсии
1. Если с – константа, то
![]() .
.
2. Если с – константа, Х – СВ, то
![]() .
.
3. Если Х и Y – произвольные СВ, то
![]() ,
,
![]() .
.
Если Х и Y не коррелированные, то
![]() .
Или
.
Или![]() – независимые СВ, то
– независимые СВ, то
 .
.
По статистике
1.1. Выборка и статистический ряд
Пусть некоторая СВ Х наблюдается
(измеряется) n раз, то есть
![]() – независимые СВ, имеющие тот же закон
распределения, что и СВ Х.
– независимые СВ, имеющие тот же закон
распределения, что и СВ Х.
Генеральная совокупность - все значения, которые может принимать рассматриваемая СВ Х в результате наблюдений (измерений).
Выборкой
![]() из генеральной совокупности называются
результаты n последовательных
независимых наблюдений (измерений) СВ
Х.
из генеральной совокупности называются
результаты n последовательных
независимых наблюдений (измерений) СВ
Х.
Вариационным рядом выборки
![]() называется запись её элементов в порядке
не убывания.
называется запись её элементов в порядке
не убывания.
Размах выборки – разность между максимальным и минимальным элементами выборки.
