Издержек производства.
3.3.Определенный интеграл с переменны верхним пределом
Функция
вида
,
где x
называется интегралом c
переменным верхним пределом
Теорема:
Если
непрерывна на
,
то производная функции
, существует в каждой точке
на
, причем
3.4Формула Ньютона-Лейбница (вывод)
Теорема:
Если
непрерывна на
, справедлива формула Ньютона-Лейбница:
ВЫВОД ФОРМУЛЫ:
Рассмотрим
, т.к.
,
то
-
первообразная для
.
Но
,
также первообразная. Это значит что
имеет место следующее равенство :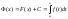
Подставим верхнюю границу:
подставами
вместо
:
в
силу 1-го свойства, что значении
определенного интеграла не зависит от
обозначения переменной интегрирования,
запишем:
3.5.Интегрирование по частям и замена переменной в определенном интеграле
Формула интегрирования по частям для определенном интеграла.
Пусть
заданны
тогда имеет место интегрирование по
частям:
→
Замена переменной в определенном интеграле.
Пусть
непрерывна на
,
а
непрерывна на
.
Вместе со своей производной
;
причем
,
и сложная функция
непрерывна
на
,
тогда справедливо формула замены
переменной для определенного интеграла:
3.6.Геометрические приложения определенного интеграла
3.6.1.Вычисление площадей плоских фигур:
1.
на
и
2.
на
и
3.
на
график имеет вид
4.
даны две функции:
и
на промежутке
5.
на промежутке
то получаем
6.
и
на промежутке
(графики ориентированы на
)
7.вычисление
площади плоской фигуры заданной системе
координат. В полярной системе точка это
пара чисел
,
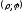любая линия равна
.
Уравнение Лемниската-Берлуни
9.
Вычисление длины дуги кривой. Пусть
заданна
на
.
3.8.Несобственные(н/с) интегралы.
1)интегралы с бесконечными пределами
А) н/с интеграл с бесконечным верхним пределом инт.
О1.
У=f(x),
хЄ[a;+)
, где а- конечное число. Ф-ция f(x) и
интегрируема на любом отрезке [а;B]
[a;+).
(1)
--н/с интеграл с бесконечным верхним
пределом
Иногда (1) называют н/с и. первого рода
О2. Если предел в правой части равенства (1) сущ. и явл. конечным числом, то н/с интеграл назыв. сходящимся, в противном случае – расходящимся
Б) н/с интеграл с бесконечным нижним пределом
О3. у= f(x) (-∞;b), которая определена и интегрируемана [А;В]с(-∞;b)
(2)
--н/с
интеграл с бесконечным нижним пр.
О4. понятие сходимости аналогично
В) н/с интеграл с двумя бесконечн. пределами интегр.
О5. у=f(x) (-∞;+∞), (А;В)с(-∞;+∞)
(3)
--н/с
интеграл с 2мя бесконечн пределами
Можно переписать как
(4)
где
-∞<С<+∞ , (3)=(4)
Исследование
сходимости интеграла
1)
α=-1, тогда
2)
α=-1
интеграл расходится
Вывод: н/с интеграл сходится если α<-1, расходится если α≥-1
2)И. на конечном промежутке
А)пусть ф-ция f(x) определена на конечном промежутке a,b) и интегрируема на любом отрезке a,a,b)
иногда это выражение называют н/с и. второго рода.
Если
конечн предел сущ., то и.
наз.
сходящимся, в противном случае –
расходящимся.
Б)н/с интеграл от разрывных функции
пусть
задана ф-ция у=f(x)
[a;b],
причем c[a;b],
такая, что ф-ции f(x) в этой точке имеет
бесконечный разрыв (x=c
– точка разрыва второго рода) , тогда
--н/с
интеграл от разрывной ф-ции
Если оба предела в правой части существуют и явл конечными числами, то н/с интеграл разрывн ф-ции назыв сходящимся, а если один из пределов не сущ. или =∞, то н/с интеграл наз. расходящимся