2.1.Неопределенный интеграл, первообразная и их св-ва.

Пусть функции f(x) и F(x) определены на интервале (a;b). Если функция F(x) имеет производную на интервале (a;b) и для всех x € (a;b) выполняется равенство F’(x) = f(x), то функция F(x) называется первообразной функции f(x) на интервале (a;b).

Совокупность всех первообразных функции f(x) на интервале (a;b) наз. неопределенным интегралом от функции f(x) на этом интервале и обозначается

2.2.Св-ва НИ:

2.4.Интегрирование путем замены переменной(подстановкой)

∫f(x)dx= [x=φ(t),t=ψ(x),dx=φ’(t)dt] =∫f(φ(t)φ’(t)dt

Если интеграл непосредственно не вычисляется,можно применить метод,кот. состоит в след.:

-вводится новая переменная

x=φ(t),где t=ψ(x) явл. обратной по отношению к φ(t), dx=φ’(t)dt- дифференциал ф-ции x=φ(t)

Если подстановка выбрана удачно,то интеграл,полученный в правой части.вычисляется проще,чем в исходной.

Если ф-ция x=φ(t) непрерывна и монотонна,то обратн. t=ψ(x) всегда сущ.

Вычислив интеграл в правой части по t,следует вернуться к переменной x

∫f(ψ(x)) φ’(x)dx=∫f(t)dt, где t=ψ(x)

1 ∫f(ax+b)dx= ax+b=t, x=(t-b)/a

dx=1/a dt

=∫f(t)1/a dt=1/a ∫f(t)dt=1/a F(t)+C=

=1/a F(ax+b)+C

2 ∫ f’(x)/f(x) dx= ln f(x) +C

3 ∫ df(x)/f(x) = ln f(x) +C

Метод интегрирования по частям

U=U(x), V=V(x)

d(UV)=VdU+UdV

проинтегрируем обе части уравнения:

∫ d(UV)= ∫ VdU+ ∫ UdV

UV=∫ VdU+ ∫ UdV=> ∫UdV=UV-∫VdU- формула интегрирования по частям

Смысл ф-лы интегрирования по частям состоит в след.:подинтегральное выраж-е

UdV разбивается на 2 части таким образом,чтобы интеграл в правой части вычислялся проще,чем исходный.

Основные классы ф-ций,интегрируемых по частям:

1 ∫ ln^m(x)dx, ∫arcsin^mxdx, ∫arccos^m xdx,∫arctg^m xdx

2 ∫Pn(x)lnaxdx,∫Pn(x)e^axdx,∫ Pn(x)sinaxdx,

∫Pn(x)cosaxdx

3 ∫e^axsinbxdx,∫e^axbxdx

4 ∫ (x²+a²)½dx, ∫(a²- x²)½dx, ∫ dx/(x²+a²)^k

3.7.Определенный интеграл в экономических и физических задачах

1)Вычисление объема произведенной продукции. Известно, что производительность труда в течение рабочего дня меняется. Предположим, что известна непрерывная функ­ция f(x), которая характеризует измерение производительности от вре­мени . Определить объем продукции, произведенной рабочим за про­межуток времени от t₁ до t₂. Решение. Искомый объем можно рассматривать как сумму объемов продукции, произведенной за бесконечно малые отрезки вре­мени. Возьмем разбиение x_k отрезка t₁,t₂. В этом случае предел интегральных сумм при диаметре d0 разбиенийx_k отрезка t1,t2 даст искомый объем продукции. Этот предел существует, так как функция f(x) непрерывная, т.е.

2)Определение средних значений

вспомним теорему о среднем значении, т.е. формулу

Число 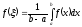называется средним значением ф-ции f(x) на отрезке a,b. На практике нередко вычисляются такого рода средние значения как средняя пр-ность труда, ср. мощность электродвигателей и т.д.