1.5.Экстремум функции двух переменных

Необходимые условия экстремума

О. Пусть функция z = f(x,y) определена в некоторой 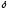- окрестности точки 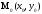. Тогда функция z = f(x,y) имеет в точке 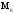максимум(минимум), если для всех точек этой окрестности выполняется неравенство

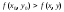
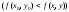
Т.(необходимое условие экстремума)

Пусть функция z = f(x,y) имеет экстремум в точке 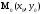. Тогда если в этой точке существуют конечные частные производные первого порядка, то они равны нулю.

Как и в случае функции одной переменной, точки, в которых все частные производные первого порядка равны нулю, называются критическими или точками, подозрительными на экстремум.

Заметим, что равенство нулю частных производных первого порядка – условие недостаточное. Действительно, рассмотрим, например, функцию z = xy. Частные производные 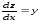и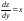равны 0 в точке (0,0), однако она не является точкой экстремума (так как в ее окружности функция z = xy может принимать и положительные значения).

Т.(достаточные условия экстремума)

Пусть функция z = f(x,y) дифференцируема в точке 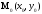, причем 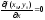и 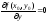имеет в ней и в некоторой ее 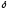- окрестности частные производные второго порядка:

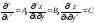Тогда если определитель второго порядка

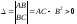, То в точке 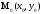функция z = f(x,y) имеет экстремум, причем если A<0, -максимум, а если A>, - минимум. В случае AC-B²<0 функция z = f(x,y) экстремума не имеет. В случае AC-B²= 0 требуется дополнительны исследования.

Наибольшее и наименьшее значение функции 2-х переменных

Наибольшее и наименьшее значение функции двух переменных z = f(x,y) в непрерывном на некотором замкнутом множестве Х (глобальный max и глобальный min) достигают в точках или в точках экстремумов, или на границе области.

Условный экстремум

Пусть дана функция 2-х переменных z = f(x,y), аргументы которой х и у связаны соотношением g(x,y)=0(которое называется уравнением связи). Тогда задача нахождения экстремума функции z = f(x,y) при условии, что g(x,y)=0, называется задачей на условный экстремум.

а) Один из алгоритмов решения этой задачи сводится к

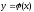
z = f(x,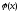), получаем функцию одной переменной.

б) Метод множителей Лагранжа

Строим функцию

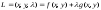-функция 3-х переменных

Находим частные производные:

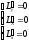Находим точки экстремумов

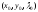
Далее - проверка достаточности условий для функции 3-х переменных.

1.6.(**)Метод наименьших квадратов. Выравнивание эмпирических данных по прямой

На практике часто приходится решать задачи сглаживанию экспериментальных зависимостей

Пусть существует зависимость для 2-х переменных, выраженная с помощью таблицы, полученной экспериментально

X … …

Y … …

Требуется наилучшим образом сгладить экспериментальную зависимость между переменными х и у, т.е. установить зависимость между х и у в виде формулы y = f(x).

О. Формулы, служащие для аналитических представлений экспериментальных данных, называются эмпирическими.

Задача нахождения эмпирических формул разбивается на 2 этапа.

I этап

Устанавливается вид зависимости y = f(x) (линейная, квадратичная, логарифмическая и т.д.).

II этап

Определяется неизвестные параметры этой функции

Для этого применяют наиболее распространенный и теоретически обоснованный метод наименьших квадратов.

Он состоит в следующем:

В качестве неизвестного параметра функции f(x) выбирают такие значения, чтобы суммы квадратов невязок (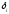) была минимальной.

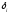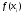(**)Невязка () – это отклонение от «теоретических» значений найденных по эмпирическим формулам y = f(x) от соответствующих опытных значений .

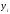Рассмотрим функцию

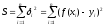(т.е. сумму квадратов всех невязок)

Пусть в качестве функций у = f(x) взята линейная функция у = ax + b. Тогда задание сводится к отыскиванию параметров a и b, при которых функция

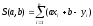
Принимает наименьшее значение. Очевидно, что S = S(a,b) есть функция 2-х переменных a и b, а 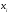и 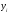- постоянные числа, полученные экспериментально.

Таким образом, достаточно исследовать функцию S = S(a,b) на экстремумах.

Находим частные производные

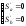или

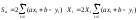
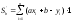
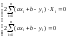
После преобразований, система принимает вид:

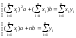(**) Система (**) - система нормальных уравнений

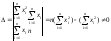(**) т.к квадрат ∑ >∑-мы квадратов

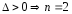
S = S(a,b) достигает своего min при a и b, найденных из системы (**). Для этого проверим достаточные условия экстремума:

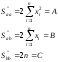
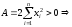функция достигает min (глобальный min).
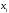
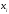
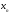
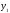
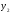
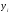