1.1.Понятие функции многих переменных

Пусть имеется n-перем-х и каждому х₁, х₂… х_n из нек-го множ-ва х поставлено в соответствие опред. число Z, тогда на множ-ве х задана ф-ция Z=f(х₁, х₂… х_n) многих переменных.

Х – обл-ть опред-я ф-ции

х₁, х₂… х_n – независ-е переем-е (аргументы)

Z – ф-ция Пример: Z=П х²₁*х₂ (Объем цилиндра)

Рассм-м Z=f(х;у) – ф-цию 2-х перем-х (х₁, х₂ замен-ся на х,у). Рез-ты по аналогии переносятся на др. ф-ции многих перем-х. Обл-ть опред-я ф-ции 2-х перем-х – вся корд пл-ть (оху) или ее часть. Мн-во знач-й ф-ции 2-х перем-х – поверх-ть в 3х-мерном простр-ве.

Приемы построения графиков: - Рассм-т сечение поверх-ти пл-тями || координатным пл-тям.

Пример: х = х₀, зн. пл-ть Х || 0уz у = у₀ 0хz Вид ф-ции: Z=f(х₀,y); Z=f(x,у₀)

Например: Z=x²+y²-2y

Z= x²+(y-1)²-1 x=0 Z=(y-1)²-1 y=1 Z= x²-1 Z=0 x²+(y-1)²-1

Парабола окруж-ть(центр(0;1)

1.2.Пределы и непрерывность ф-ций двух переменных

Пусть задана Z=f(х;у), тогда А – предел ф-ции в т.(х₀,y₀), если для любого сколь угодно малого положит. числа E>0 сущ-т полож-е число б>0, что для всех х,у удовл-щих |x-х₀|<б; |y-y₀|<б выполняется нерав-во |f(x,y)-A|<E

Z=f(х;у) непрерывна в т.(х₀,y₀), если: - она опред-на в этой т.; - имеет конеч. предел при х, стрем-ся к х₀ и у к у₀; - этот предел = знач-ю

ф-ции в т.(х₀,y₀), т.е. limf(х;у)=f(х₀,y₀)

Если ф-ция непрерывна в кажд. т. мн-ва Х, то она непрерывна в этой области

Дифференциал ф-ции, его геом смысл. Применение диф-ла в приближенных значениях.

dy=f’(x)∆x – диф-л ф-ции

dy=dx, т.е. dy=f ’(x)dx если у=х

С геом точки зрения диф-л ф-ции – это приращение ординаты касательной, проведенной к графику ф-ции в точке с абсциссой х₀

х₀ х₀+dx

Диф-л применяют в вычислении приближ. значений ф-ции по формуле: f(х₀+∆x)~f(х₀)+f’(х₀)∆x

Чем ближе ∆x к х, тем результат точнее

1.3.Частные производные первого и второго порядка

Производная первого порядка(которая называется частной)

О. Пусть х, 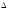у – приращения независимых переменных х и у в некоторой точке из области Х. Тогда величина, равная z = f(x+х, y+у) = f(x,y) называется полным приращением в точке х_0,у_0.Если переменную х зафиксировать, а переменной у дать приращение у, то получим zу = f(x,y,+ у) – f(x,y)

Аналогично определяется частная производная от переменной у, т.е.

z’_x =

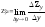
Частную производную функции 2-х переменных находят по тем же правилам, что и для функций одной переменной.

Отличие состоит в том, что при дифференциации функции по переменной х , у считается const, а при дифференцировании по у, х считается const.

Изолированные const соединены с функцией операциями сложения/вычитания.

Связанные const соединены с функцией операциями умножения/деления.

Производная изолированной const = 0

1.4.Полный дифференциал функции 2-х переменных и его приложения

Пусть z = f(x,y), тогда

tz = - называется полным приращением

Частная производная 2-го порядка

Для непрерывных функций 2-х переменных смешанные частные производные 2-го порядка и совпадают.

Применение частных производных к определению частных производных max и min функций называются экстремумами.

О. Точки называются max или min z = f(x,y), если существуют некоторые отрезки 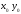такие, что для всех x и y из этой окрестности f(x,y)<f или

f(x,y)>f .

Т. Если задана точка экстремума функции 2-х переменных , то значение частных производных в этой точке равны 0, т.е. ,

Точки , в которых частные производные первого порядка называются стационарными или критическими.

Поэтому для нахождения точек экстремума функции 2-х переменных используются достаточные условия экстремума.

Пусть функция z = f(x,y) дважды дифференцируема, и стационарная точка,

A = B = C =

, тогда

1), причем maxA<0, minA>0.

2)

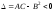
3)

1.4.(*)Полный дифференциал. Геометрический смысл дифференциала. Приложение дифференциала в приближенных вычислениях

О. Пусть функция y = f(x) определена в некоторой окрестности в точки . Функция f(x) называется дифференцируемой в точке , если ее приращение в этой точке , где представлено в виде (1)

Где А – постоянная величина, не зависящая от , при фиксированной точке х, - бесконечно малая при . Линейная относительно функция А называется дифференциалом функции f(x) в точке и обозначается df() или dy.

Таким образом, выражение (1) можно записать в виде ().

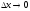Дифференциал функции в выражении (1) имеет вид dy = A. Как и всякая линейная функция, он определен для любого значений в то время, как приращение функции необходимо рассматривать только для таких , для которых + принадлежит области определения функции f(x).

Для удобства записи дифференциала приращение обозначают dx и называют его дифференциалом независимой переменной x. Поэтому дифференциал записывают в виде dy = Adx.

Если функция f(x) дифференцируема в каждой точке некоторого интервала, то ее дифференциал является функцией двух переменных – точки x и переменной dx:

Dy = Adx

Т. Для того, чтобы функция y = g(x) была дифференцируема в некоторой точке , необходимо и достаточно, чтобы она имела в этой точке производную, при этом

(2)

(*)Доказательство. Необходимость.

Пусть функция f(x) дифференцируема в точке , т.е. . Тогда

Поэтому производная f’() существует и равна А. Отсюда dy = f’()dx

Достаточность.

Пусть существует производная f’(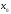), т.е. = f’(). Тогда

Где - бесконечно малая и . Значит, для имеем

(3)

А так как - величина бесконечно малая, то наличие равенства (3) и означает дифференцируемость функции в точке .

Формула (2) позволяет находить дифференциалы функций, если известны их производные. Так, например, используя производные некоторых элементарных функций, получаем : dc = 0 (с - постоянная), dsinx = cosxdx, и т.д.

Геометрический смысл дифференциала функции в точке - это приращение ординаты касательной к кривой в этой точке.

Если предположить, что функция y =f(x) сложная, т.е. , то производная

примет вид согласно правилам нахождения производной сложной функции. В этом случае выражение (2) можно записать так:

(*) где - сложная функция.

Приближенное вычисление с помощью дифференциала.

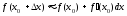Согласно выражению (1), приращение функции f(x) можно записать в виде , откуда (4)

Формула (4) служит для приближенных вычислений значений функции в заданной точке. По сути дела это уравнение касательной к кривой y = f(x) в точке , т.е. мы приближенно заменяем на участке кривую y = f(x) отрезком касательной. Для вычисления значения функции в точке х берут в некоторой ее окрестности точку , такую, что не составляет труда найти f() и f’()/