Примерный вариант контрольной работы №7

1. Найти область определения функции z = ln( x-y ).

2. Найти частные производные функции z = x³+2xy²+x²y-2 в точке A(1; 2) и производную по направлению вектораl, идущему от точки A к точке B=(2; 1).

3. Вычислить приближенно, с помощью дифференциала ( 0,98 )²( 1,04 )².

4. Найти все вторые частные производные функции

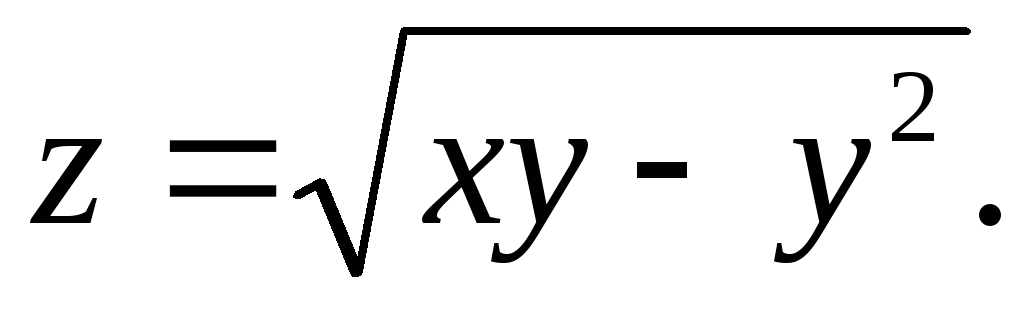
5. Найти экстремумы функции z = 2x²- y²+xy-2x.

Дифференциальные уравнения

Пример 28. Решить задачу Коши:

Решение. 1) Найдем общее решение дифференциального уравнения. Данное уравнение первого порядка является линейным. Следовательно, произведем следующую замену переменной:

Тогда

Подберем теперь такую функцию v(x), чтобы v+2xv=0. То есть v(x) будем искать как решение дифференциального уравнения с разделяющимися переменными:

При С = 0 получим: ln| v | = -x². Следовательно, .

При таком выборе функции v(x) исходное дифференциальное уравнение примет вид:

Следовательно, Таким образом,

2) Для решения задачи Коши воспользуемся начальным условием y(0)=0.

Тогда

Ответ: .

Теория вероятностей Случайные события

Пример 29. На склад хлебозавода поступило 20 мешков муки высшего сорта и 10 мешков первого сорта. Наудачу берут три мешка. Какова вероятность того, что все они первого сорта?

Решение. Пусть А – искомое событие. Всего на склад поступило 20+10=30 мешков. Три мешка можно выбрать из 30 числом сочетаний из 30 по 3, значит n=, среди них благоприятствующих случаев равно числу сочетаний из 10 по 3, значит m=. По классическому определению вероятности имеем

P(A)=== .

Пример 30. Ребенок играет с шестью буквами азбуки: А, А, Е, К, Р, Т. Найти вероятность того, что он сможет сложить случайно слово КАРЕТА (событие А).

Решение. Решение осложняется тем, что среди букв есть одинаковые – две буквы "А". Поэтому число всех возможных случаев в данном испытании равно числу перестановок с повторениями из 6 букв:

.

Эти случаи равновозможны, попарно несовместны и образуют полную группу событий, т.е. образуют схему случаев. Лишь один случай благоприятствует событию А. Поэтому

.

Пример 31. Таня и Ваня договорились встречать Новый год в компании из 10 человек. Они оба очень хотели сидеть рядом. Какова вероятность исполнения их желания, если среди их друзей принято места распределять путем жребия?

Решение. Обозначим через А событие "исполнение желания Тани и Вани". 10 человек могут усесться за стол 10! разными способами. Сколько же из этих

n = 10! равновозможных способов благоприятны для Тани и Вани? Таня и Ваня, сидя рядом, могут занять 20 разных позиций. В то же время восьмерка их друзей может сесть за стол 8! разными способами, поэтому m = 20  8!. Следовательно,

.

Пример 32. Группа из 5 женщин и 20 мужчин выбирает трех делегатов. Считая, что каждый из присутствующих с одинаковой вероятностью может быть выбран, найти вероятность того, что выберут двух женщин и одного мужчину.

Решение. Общее число равновозможных исходов испытания равно числу способов, которыми можно выбрать трех делегатов из 25 человек, т.е. . Подсчитаем теперь число благоприятствующих случаев, т.е. число случаев, при которых имеет место интересующее нас событие. Мужчина-делегат может быть выбран двадцатью способами. При этом остальные два делегата должны быть женщинами, а выбрать двух женщин из пяти можно . Следовательно, . Поэтому

.

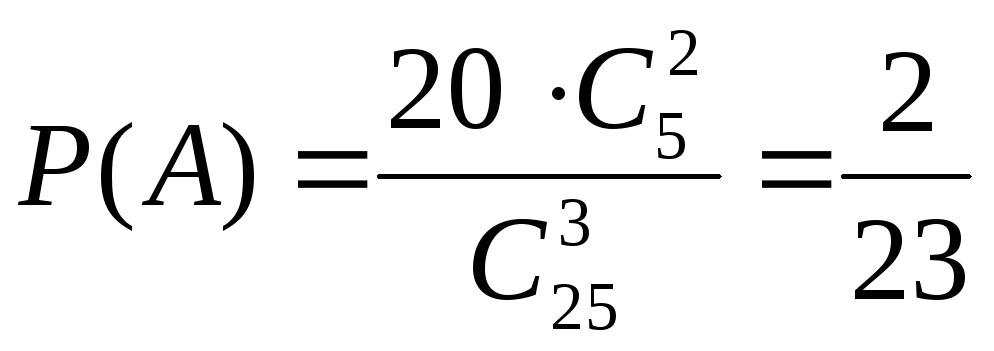Пример 33. Стрелок производит один выстрел по мишени. Вероятность выбить 10 очков (событие А), 9 очков (событие В), и 8 очков (событие С) равны соответственно 0,11; 0,23; 0,17. Найти вероятность того, что при одном выстреле стрелок выбьет менее 8 очков (событие D).

Решение. Перейдем к противоположному событию - при одном выстреле стрелок выбьет не менее 8 очков. Событие наступает, если произойдет А или В, или С, т.е. =А+В+С. Так как события А,В,С попарно несовместны, то, по теореме сложения,

P() = P(А) + P(В) + P(С) = 0,51.

Откуда

Р(D) = 1- P( ) = 1 – 0,51 = 0,49.

Пример 34. От коллектива бригады которая состоит из 6 мужчин и 4 женщин, на профсоюзную конференцию выбирается два человека. Какова вероятность, что среди выбранных хотя бы одна женщина (событие А).

Решение. Если произойдёт событие А, то обязательно произойдёт одно из следующих несовместных событий: В – “выбраны мужчина и женщина”; С – “выбраны две женщины”. Поэтому можно записать: А = В + С. Найдём вероятность событий В и С. Два человека из 10 можно выбрать С²₁₀ способами. Двух женщин из четырёх можно выбрать С²₄ способами. мужчину и женщину можно выбрать 6*4 способами. Тогда P(B) = 4 * 6/ С²₁₀, P(C) = С²₁₀ /С²₄. Так как события В и С несовместны, то, по теореме сложения,

P(A) = P(B + C) = P(B) + P(C) = 8/15 + 2/15 = 2/3.

Пример 35. Из урны, в которой 5 белых и 10 черных шаров, вынимают подряд два шара. Найти вероятность того, что оба шара белые (событие А).

Решение. Рассмотрим события: В – первый вынутый шар белый; С – второй вынутый шар белый. Тогда А = ВС.

Опыт можно провести двумя способами:

1) с возвращением: вынутый шар после фиксации цвета возвращается в урну. В этом случае события В и С независимы:

Р(А) = Р(В)  Р(С) = 5/155/15 = 1/9;

2) без возвращения: вынутый шар откладывается в сторону. В этом случае события В и С зависимы:

Р(А) = Р(В)  Р(С/В) .

Для события В условия прежние, , а для С ситуация изменилась. Произошло В, следовательно в урне осталось 14 шаров, среди которых 4 белых.

.

Итак,

.

Пример 36. Среди 50 электрических лампочек 3 нестандартные. Найти вероятность того, что две взятые одновременно лампочки нестандартные.

Решение. Рассмотрим события: А – первая лампочка нестандартная,

В – вторая лампочка нестандартная, С – обе лампочки нестандартные. Ясно, что С = А  В. Событию А благоприятствуют 3 случая из 50 возможных, т.е. Р(А) = 3/50. Если событие А уже наступило, то событию В благоприятствуют два случая из 49 возможных, т.е. Р(В/А) = 2/49. Следовательно,

.

Пример 37. В корзине яблоки с четырех деревьев одного сорта. С первого – 15% всех яблок, со второго – 35%, с третьего – 20%, с четвертого – 30%. Созревшие яблоки составляют соответственно 99%, 97%, 98%, 95%.

а) Какова вероятность того, что наугад взятое яблоко окажется спелым (событие А).

б) При условии, что наугад взятое яблоко оказалось спелым, вычислить вероятность того, что оно с первого дерева.

Решение. а) Имеем 4 гипотезы:

Н₁ – наугад взятое яблоко снято с 1-го дерева;

Н₂ – наугад взятое яблоко снято с 2-го дерева;

Н₃ – наугад взятое яблоко снято с 3-го дерева;

Н₄ – наугад взятое яблоко снято с 4-го дерева.

Их вероятности по условию: Р(Н₁) = 0,15; Р(Н₂) = 0,35; Р(Н₃) = 0,2;

Р(Н₄) = 0,3.

Условные вероятности события А:

Р(А/Н₁) = 0,99; Р(А/Н₂) = 0,97; Р(А/Н₃) = 0,98; Р(А/Н₄) = 0,95.

Вероятность того, что наудачу взятое яблоко окажется спелым, находится по формуле полной вероятности:

Р(А) = Р(Н₁)  Р(А/Н₁) + Р(Н₂)  Р(А/Н₂) + Р(Н₃)  Р(А/Н₃) + Р(Н₄)  Р(А/Н₄) =

= 0, 969.

б) Формула Байеса для нашего случая имеет вид:

.

Пример 38. Найти интегральную функцию распределения случайной величины Х, заданной рядом распределения:

Х	1	2	3
Р	0,3	0,2	0,5

и построить ее график.

Решение. Пусть х  1, тогда F(x) = 0, так как событие Х < х будет невозможным. Если 1< х  2, то по определению интегральной функции распределения имеем F(x) = p₁ = 0,3. Если 2< х  3, то F(x) = p₁ + p₂ = 0,5. Если х > 3, то

F(x) = p₁ + p₂ + p₃ = 1. Окончательно получаем

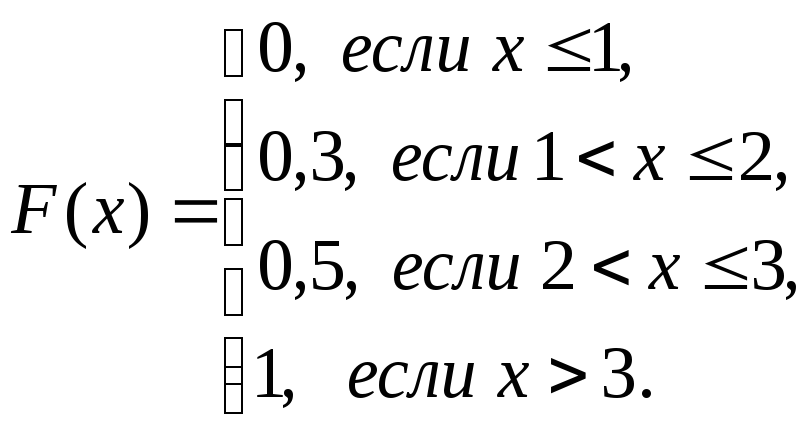
График функции F(х) изображен на рис. 4.

F(х)

1

0,5

0,3

0 1 2 3 х

Рис. 4.

Пример 39. Дискретная случайная величина Х задана законом распределения:

Х	0	1	2	3
р	0,4	0,1	0,3	0,2

Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.

Решение. Так как случайная величина является дискретной, то для вычисления М(Х) воспользуемся формулой . Имеем

М(х) = 00,4 + 10,1 + 20,3 + 30,2 = 1,3.

Найдем дисперсию D(x). Предварительно найдем математическое ожидание от х²:

М(х²) = х₁²  р₁ + х₂² р₂ + х₃² р₃ + х₄² р₄ = 0²0,4 + 1²0,1 + 2²0,3 + 3²0,2 = 3,1.

Далее по формуле получаем

D(X) = 3,1 –1,3² = 3,1 – 1,69 = 1,41.

Найдем среднее квадратическое отклонение. Имеем

(х) =.

Пример 40. Непрерывная случайная величина Х задана функцией распределения

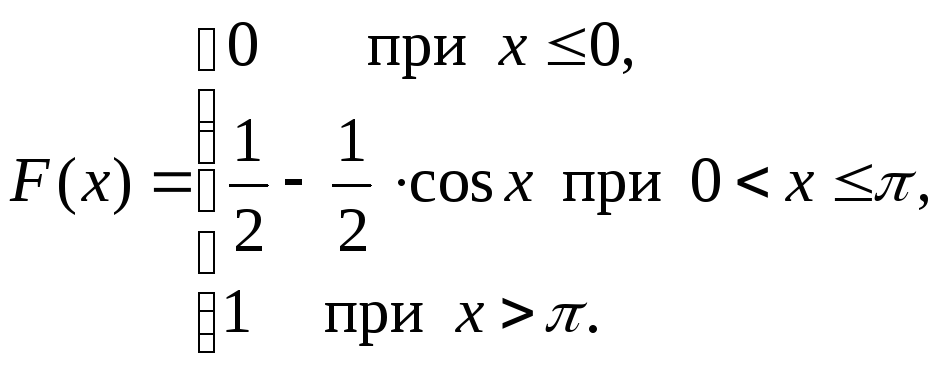
Найти математическое ожидание и дисперсию этой случайной величины.

Решение. По определению дифференциальной функции (х) = F(x). Отсюда

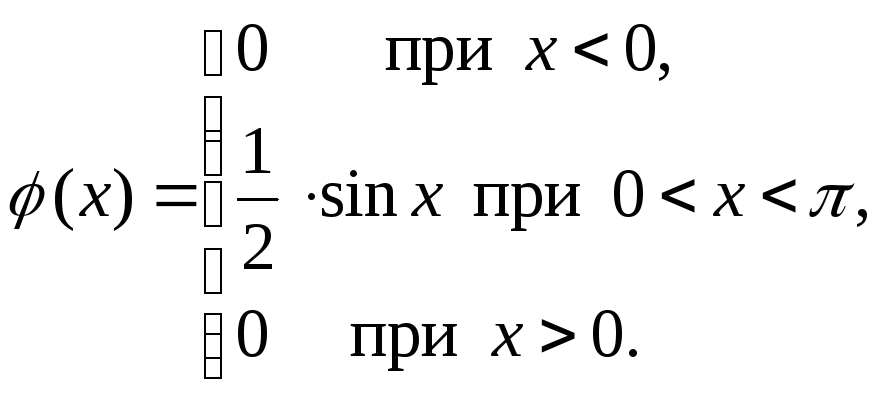
В точках х = 0 и х =  функция (х) не дифференцируема. По формуле получаем

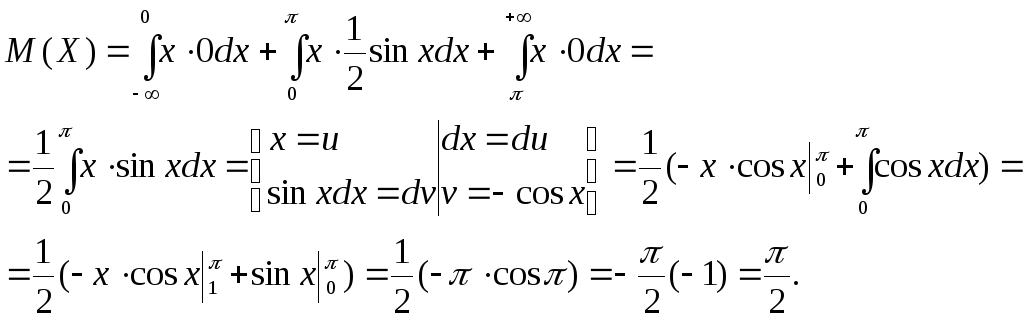
Находим сначала М(Х²). Имеем

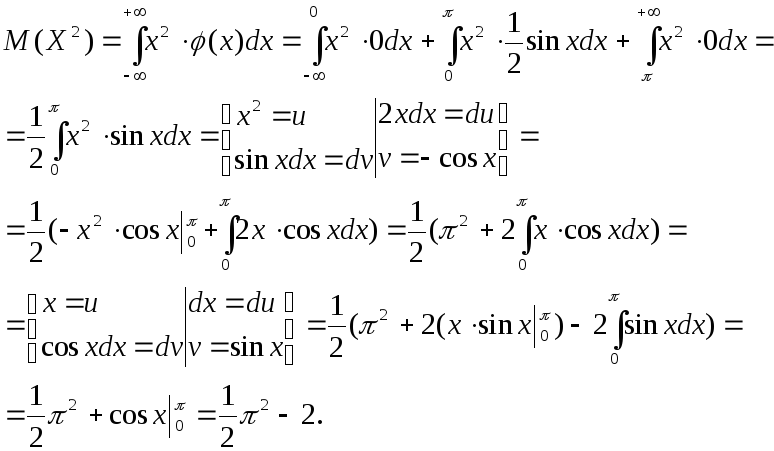
Далее по формуле получаем

.