Примерный вариант контрольной работы №1

1. Решить систему линейных уравнений: 1) методом Крамера; 2) методом

Гаусса.

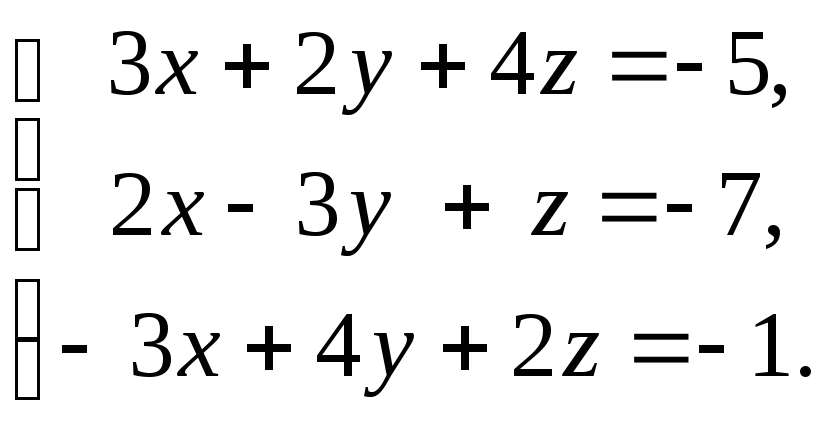
2. Найти произведение матриц AB и BA:

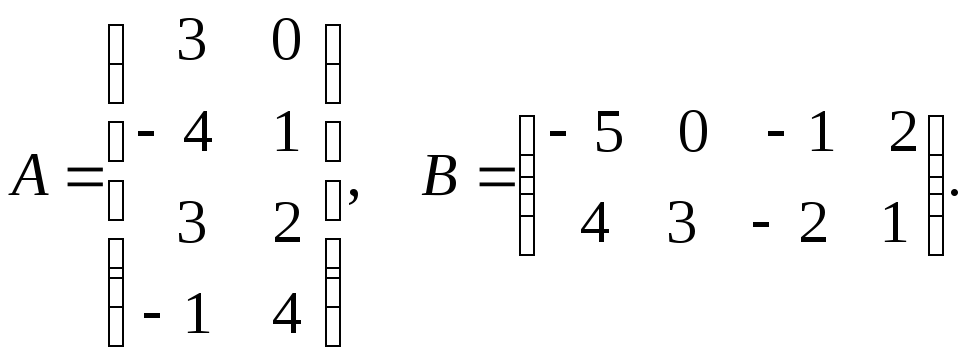
3. Найти общее решение системы:

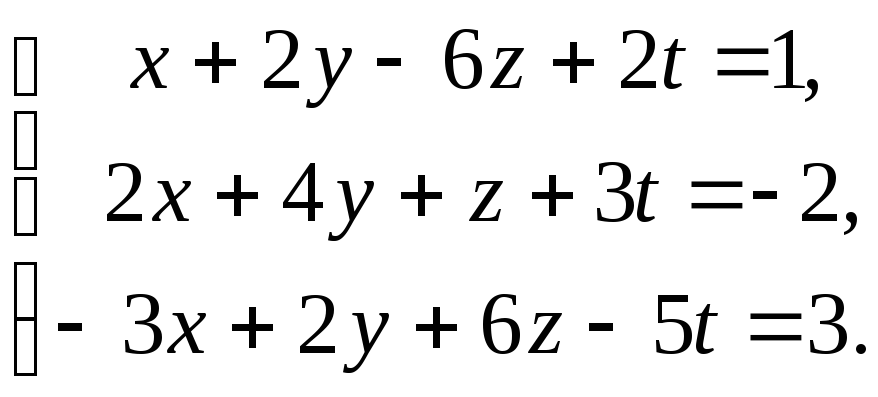
Векторная алгебра

Пример 4. Дана пирамида ABCD: A( 2; 4;-1 ), B( 3; 2; 0 ), C( 1;-3; 2 ), D( 5;-1; 3 ).

Найти: 1) угол BCD; 2) площадь грани ABC; 3) объем пирамиды.

Решение.

1. Найдем координаты векторов 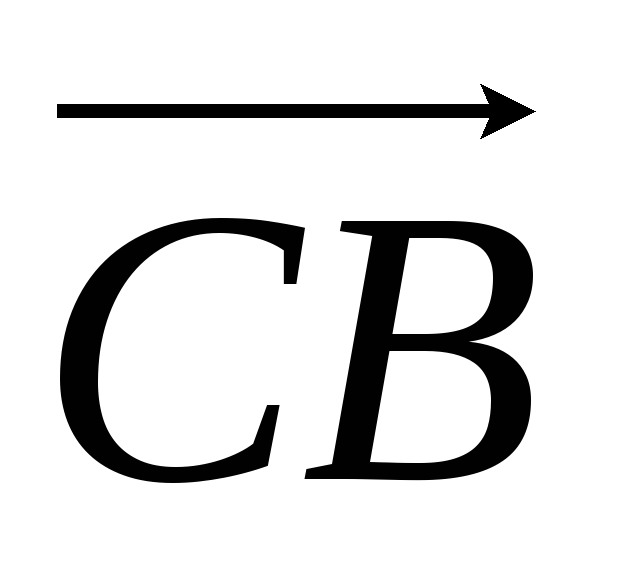и , образующих угол :

Угол BCD найдем по формуле: , где -скалярное произведение векторов и . Таким образом,

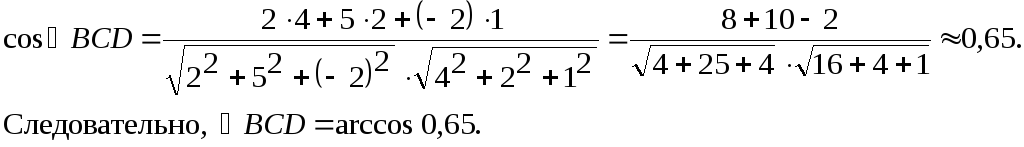
2. Площадь грани ABC находим по формуле:

, где - векторное произведение векторов и .

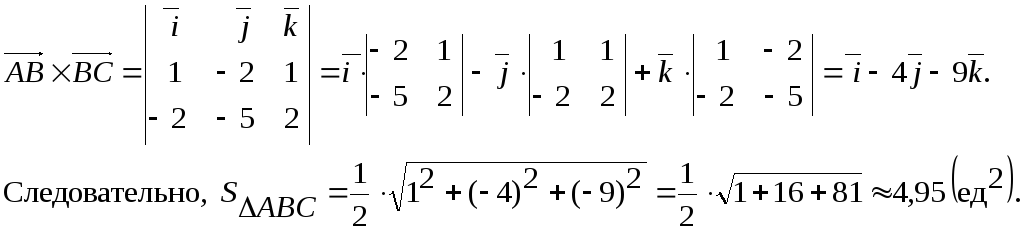
3. Объем пирамиды находим по формул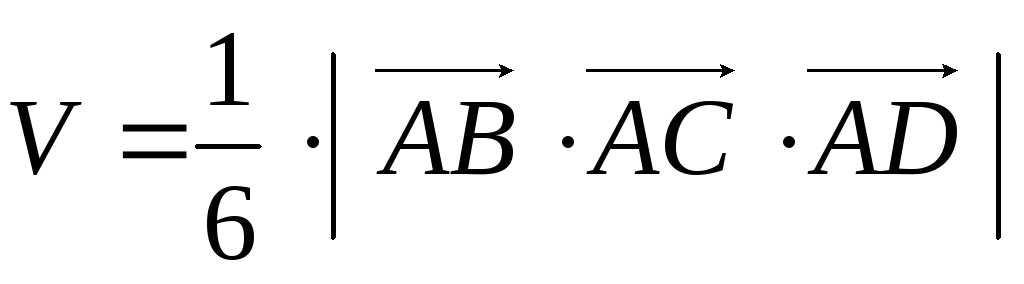е: , где

-смешанное произведение векторов

и

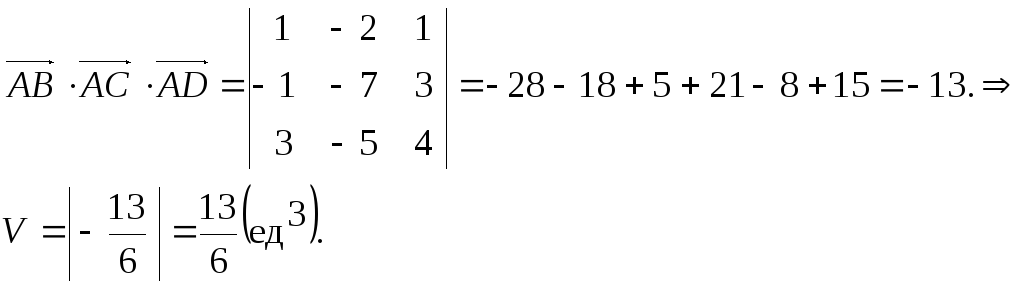
Пример 5. Дано: a =3; b =2; угол между векторами a и b равен /3.

Найти угол  между векторами

Решение. 1) Найдем скалярное произведение

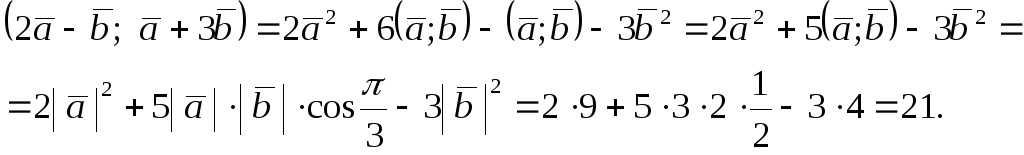
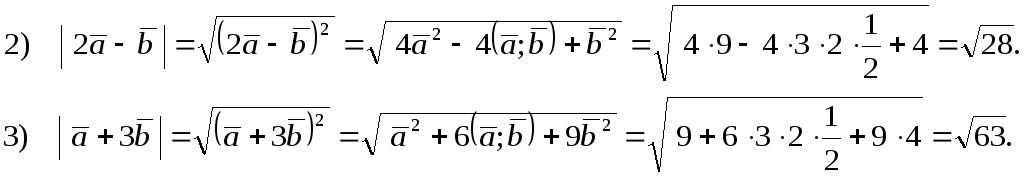
Ответ:

Примерный вариант контрольной работы №2

1. Даны вершины пирамиды: A( 2; -3; 5 ); B( 0; 6; -2 ); C( 3; 1; -5 ); D( 2; 1; 1 ).

Найти ABC; S_ABC; V_пир.

2. Доказать, что векторы a=( 2;-3; 1 ),b=( 3; 2;-4 ) иc=(-1;-5; 3 ) лежат в одной плоскости (компланарны).

Аналитическая геометрия

Пример 6. Дан треугольник A( 2; 7 ), B(-5; 7 ), C( 5; 3 ). Найти: 1) уравнения сторон; 2) уравнение и длину медианы AM; 3) уравнение и длину высоты BD; 4) уравнение биссектрисы AK; 5) точку пересечения медианы AM с высотой BD и угол между ними.

Решение.

1. Уравнения сторон AC и BC найдем, используя уравнение прямой, проходящей через две точки:

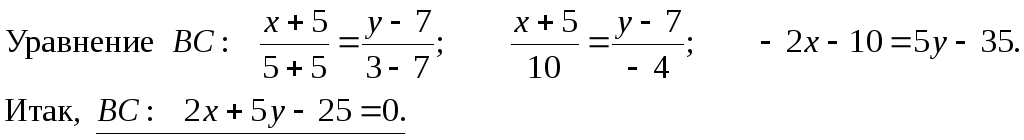
Уравнение AB находится еще проще. Нужно только заметить, что вторая координата точек A и B одинакова и равна 7.

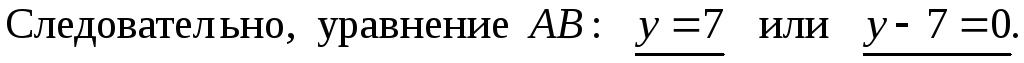2. Н айдем точку M – середину стороны BC:

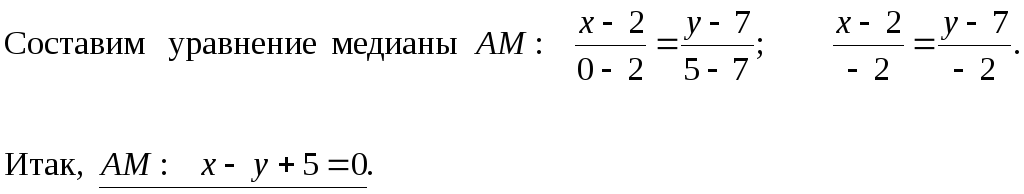
Длину медианы найдем как расстояние между двумя точками:

3. Определим угловой коэффициент стороны AC. Для этого уравнение

AC запишем в виде Следовательно,

(условие перпендикулярности прямых BD и AC).

Составим уравнение высоты BD, используя уравнение прямой, проходящей через заданную точку B и с угловым коэффициентом k:

y – y₀ = k( x - x₀ ).

Длину высоты BD найдем как расстояние точки B до прямой AC по формуле: , где ax+by+c=0 – общее уравнение прямой AC, а (x₀; y₀) – координаты точки B. Итак,

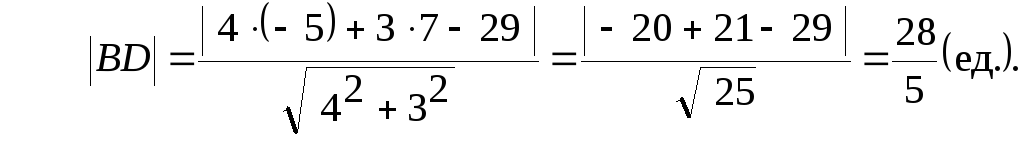
4. Найдем основание биссектрисы (точку K), используя то, что точка K делит

отрезок BC на части, пропорциональные прилежащим сторонам треугольника:

.

Следовательно,.

Для нахождения координат точки K используем формулы деления отрезка в данном отношении:

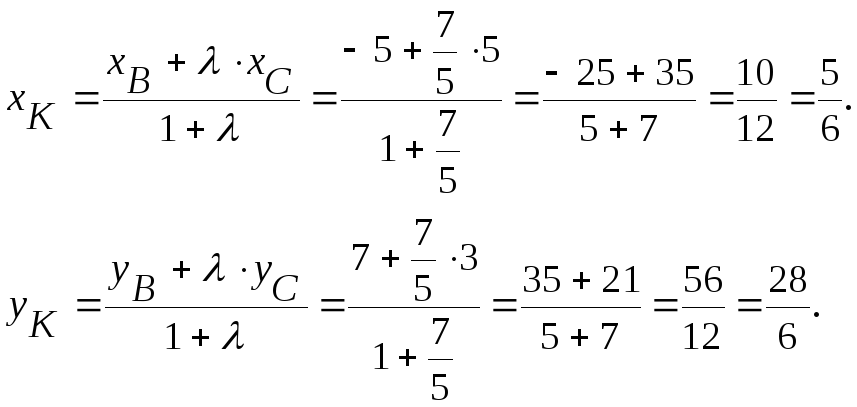
Составим уравнение AK, используя координаты точек A и K:

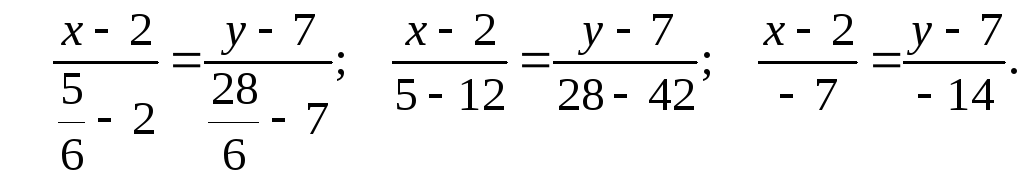
5. Найдем точку О пересечения медианы AM с высотой BD, решив систему:

.

Итак, точка O имеет координаты: O( 23; 28 ). Для нахождения угла между прямыми линиями BD и AM воспользуемся формулой:

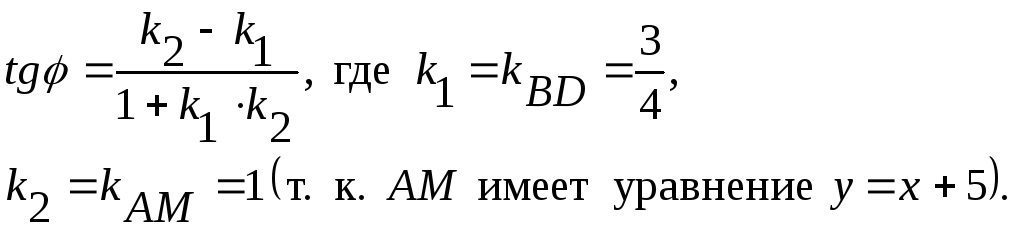
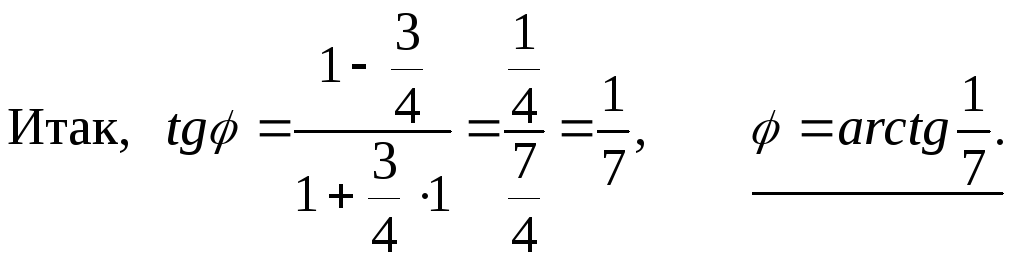
Пример 7. Найти координаты фокусов и эксцентриситет эллипса: 4x²+9y²=1.

Решение. В каноническом виде уравнение эллипса выглядит следующим образом: 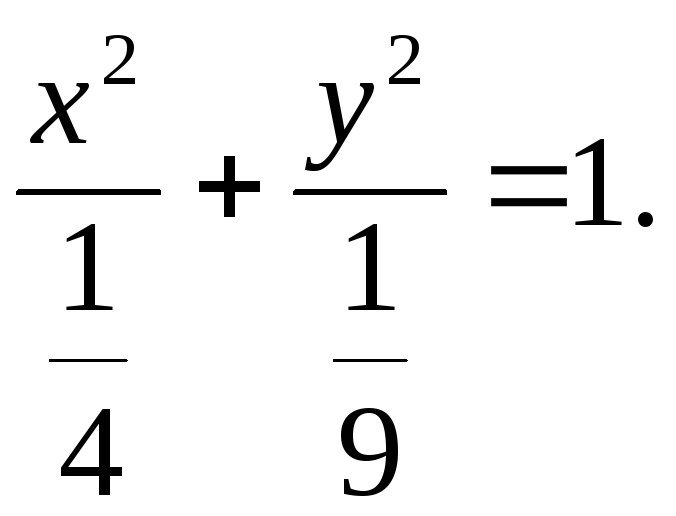Из этого уравнения видно, что большая полуось эллипса равна

а малая полуось равна Расстояние от центра эллипса до его фокусов находим по формуле: Таким образом, фокусы эллипса имеют координаты:

Эксцентриситет эллипса найдем по формуле: