
Весна 16 курс 3 ОрТОР / Теория АД / ТАДСтарков / Термодинамика и теплопередача Никифоров А.И.-2
.pdf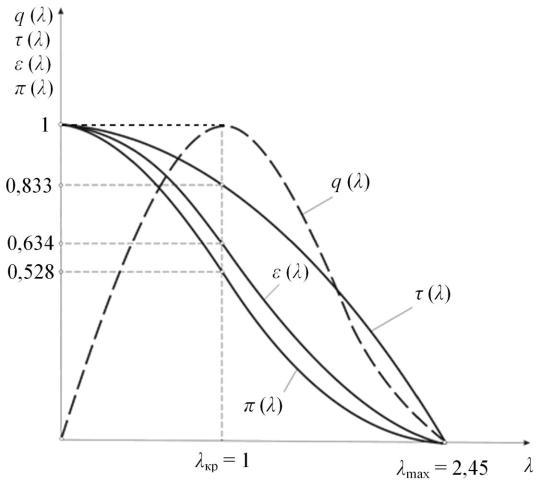
101
Рис. 8.11. Графическое изображение газодинамических функций
Таблицы газодинамических функций, заранее рассчитанные и приведенные в виде таблиц, существенно упрощают анализ и расчет газовых потоков.
Здесь рассмотрены пять наиболее употребительных газодинамических функций. В расчетах иногда используют и другие величины, описание и таблицы которых приведены в Приложении П. 4.
8.9. Идеальное течение газа в соплах. Основные положения
Рассмотрим более подробно течение газа в соплах. Как и ранее, считаем
газ идеальным, а течение — происходящим без трения и энергообмена с
102
окружающей средой. Разгон газа, как отмечалось, сопровождается понижением давления, поэтому давление газа перед соплом всегда должно быть выше, чем давление окружающей среды, в которую происходит истечение газа. На рис. 8.5, 8.8 и 8.1, в приведены схемы рассматриваемых далее суживающегося сопла и сопла Лаваля и даны обозначения их характерных сечений.
Основные определения. Располагаемой степенью понижения давления газа в сопле называется отношение полного давления газа на входе в сопло к давлению окружающей среды
с.р. |
p0* |
. |
(8.53) |
|
|||
|
pH |
|
|
Действительной степенью понижения давления газа в сопле называется отношение полного давления газа на входе в сопло к давлению в выходном сечении сопла
с |
|
p0* |
. |
(8.54) |
|
||||
|
|
pс |
|
|
Степень понижения давления газа, при которой газ разгоняется до скорости, равной местной скорости звука, называется критической,
критическая степень понижения давления газа определена формулами (8.36) и
(8.37):
|
|
p* |
k 1 |
|
k |
|
|||
|
|
|
|
|
|
||||
|
|
k 1 |
|
||||||
кр |
|
0 |
|
|
|
. |
(8.55) |
||
pкр |
|
|
|||||||
|
|
|
2 |
|
|
|
|||
Как видно (8.55), критическая степень понижения давления зависит только от показателя адиабаты k (табл. 8.1).
Таблица 8.1
Величина πкр при разных значениях k
k |
1,15 |
1,25 |
1,33 |
1,40 |
1,67 |
|
|
|
|
|
|
πкр |
1,741 |
1,802 |
1,851 |
1,893 |
2,055 |
|
|
|
|
|
|
103
Различают следующие режимы работы сопла.
1.Режим полного расширения, когда давление в выходном сечении сопла равно давлению окружающей среды: pс = pН. В этом случае, как нетрудно увидеть, πс = πср. Для сопла Лаваля такой режим работы принято называть также расчетным.
2.Режим недорасширения (неполного расширения), когда давление в выходном сечении сопла выше давления окружающей среды: pс > pН. В этом случае πс < πср, и окончательное расширение газа и понижение его давления до величины pН происходит за пределами сопла.
3.Режим перерасширения, когда давление в выходном сечении сопла ниже давления окружающей среды: pс < pН. Соответственно πс > πср. Режим перерасширения, как будет показано далее, реализуется только в сопле Лаваля.
Рассмотрим особенности изменения параметров потока газа в соплах при различных режимах его работы.
8.10. Режимы работы дозвукового сопла
Дозвуковое сопло может работать на расчетных и нерасчетных режимах.
8.10.1. Изменение параметров потока в суживающемся (дозвуковом) сопле
Рассмотрим особенности идеального течения газа в суживающемся сопле.
Поскольку рассматриваемое течение является энергоизолированным и происходящим без трения, то параметры заторможенного потока газа (Т*, p*, ρ*)
по длине сопла остаются неизменными. Падение статического давления вдоль сопла (- dp) приводит, как отмечалось, к росту скорости газа. Увеличение кинетической энергии потока в свою очередь понижает энтальпию и температуру газа. В общем случае скорость истечения из суживающегося сопла определяется по формуле (8.28):
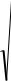
|
|
|
104 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
1 |
|
|
||
cс |
2 |
|
|
|
RT0* 1 |
|
|
|
|
, |
|
k 1 |
|
k 1 |
|||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
k |
|||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
c |
|
|||
а температура газа в выходном сечении сопла Тс — по формуле
Tс |
Т0* |
|
||||
|
|
|
. |
(8.56) |
||
|
|
k 1 |
||||
|
|
|
k |
|
|
|
|
|
c |
|
|||
Вследствие снижения температуры газа величина местной скорости звука вдоль сопла уменьшается.
Характер истечения газа из суживающегося сопла полностью определяется соотношением между величинами располагаемой и критической степеней понижения давления (πс.р и πкр). Исследуем особенности течения газа при разных соотношениях между πс.р и πкр. Для газа с неизменными физическими свойствами величина πкр постоянна (см. табл. 8.1). Поэтому соотношение между πс.р и πкр может изменяться лишь за счет увеличения или уменьшения
πс.р. Отметим, что величина πс.р может изменяться как с изменением давления перед соплом p0* , так и с изменением давления окружающей среды pН.
8.10.2. Работа дозвукового сопла на расчетном режиме
Рассмотрим расчетный режим работы сопла,
выходе из сопла pс равно давлению окружающей режиме очевидно, что
с |
p0* |
с.р. |
p0* |
кр . |
|
pс |
pН |
||||
|
|
|
при котором давление на среды pН. На расчетном
(8.57)
При данном условии в сопле происходит полное расширение газа;
давление в выходном сечении сопла равно давлению окружающей среды
(pс = pН), и поэтому действительная степень понижения давления газа в сопле равна располагаемой (πс = πс.р). Поскольку πс.р < πкр, то располагаемой степени
105
понижения давления не хватает для разгона газа до скорости звука. Скорость истечения газа из сопла в этом случае меньше скорости звука (сс < ас и Мс < 1).
Характер изменения параметров потока вдоль сопла при данном соотношении между πс.р и πкр показан на рис. 8.12, а.
При дозвуковых скоростях истечениях газа режим работы сопла всегда расчетный. Это объясняется тем, что любое изменение pН в виде волн слабых возмущений проникает внутрь сопла, вызывая изменения давления в сопле при одновременном изменении скорости.
Например: увеличение высоты полета (Н) вызывает уменьшение давления pН, тогда слабые возмущения, вызванные уменьшением pН, распространяясь навстречу дозвуковому потоку (сс < ас) внутрь сопла, «предупреждают» его об уменьшении pН. В результате происходит перестройка потока на новые условия до тех пор, пока давление pс не станет равным новому значению pН.
Одновременно из-за роста с.р. |
p0* |
произойдет увеличение скорости потока, а |
|
pH |
|||
|
|
режим работы сопла остается расчетным.
Если располагаемая степень понижения давления газа в сопле равна критической (πс = πкр), то скорость истечения газа из сопла равна местной скорости звука (сс = ас, Мс = 1). Расширение газа в сопле полное (pс = pН), и
действительная степень понижения давления газа равна располагаемой (πс = πс.р
= πкр). Такой режим работы сопла можно рассматривать как предельный из режимов с полным расширением газа в сопле, когда при полном использовании располагаемой степени понижения давления в суживающемся сопле достигается максимально возможная скорость потока.
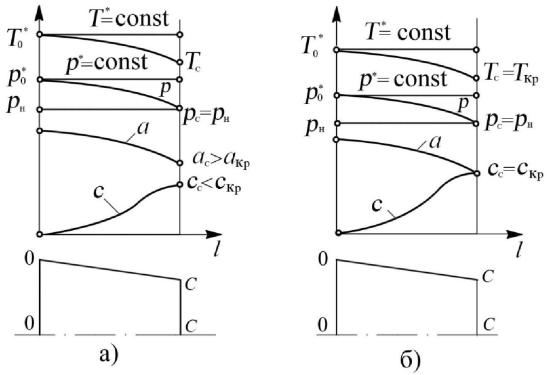
Изменение параметров потока вдоль сопла при πс.р = πкр показано на рис. 8.12, б. В выходном сечении сопла скорость и параметры потока равны критическим, которые определяются по уравнениям (8.32)—(8.35).
106
Рис. 8.12. Характер изменения параметров потока вдоль сопла:
а— при πс.р < πкр; б — при πс.р. = πкр
8.10.3.Работа дозвукового сопла на нерасчетном режиме
Нерасчетным режимом работы сопла называется такой режим, при котором давление газа на выходе из сопла больше давления окружающей среды, то есть pс > pН.
Следовательно, условие нерасчетного режима заключается в том, что располагаемая степень понижения давления газа в сопле больше критической (πс.р > πкр). Несмотря на повышение величины πс.р в области πс.р > πкр, скорость истечения газа из сопла остается равной критической (сс = ас = акр; Мс = 1), так как в суживающемся сопле нельзя разогнать поток до скорости, превышающей местную скорость звука. Соответственно температура, плотность, давление и скорость газа в выходном сечении сопла, а также величина πс остаются равными критическим значениям:
pс = pкр; Тс = Ткр; ρс = ρкр; сс = скр; πс.р = πкр.
107
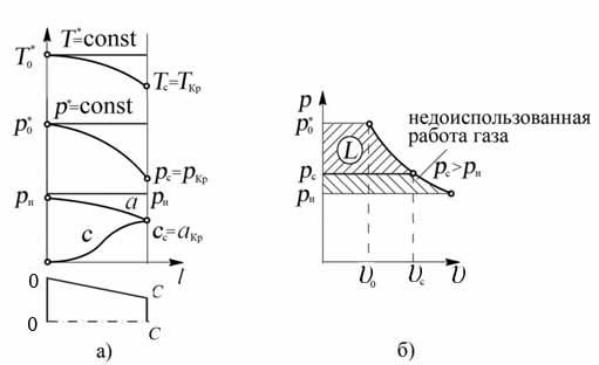
Основной особенностью данного режима работы суживающегося сопла является то, что расширение газа в сопле неполное: давление газа в выходном сечении сопла выше давления окружающей среды (pс > pН), а действительная степень понижения давления меньше располагаемой (πс < πc.р). Следовательно,
располагаемая степень понижения давления газа полностью не используется в сопле для увеличения скорости потока, газ покидает сопло, унося с собой неиспользованную энергию (рис. 8.13, б.).
В области значений πс.р > πкр изменение внешних условий не сказывается на характере течения газа в сопле. В частности, изменение давления pН и
связанное с ним изменение πс.р не влияют на параметры потока в выходном сечении сопла. Физически это объясняется тем, что возмущения в виде изменения давления распространяются в газе со скоростью звука. В случаях,
когда в выходном сечении сопла скорость истечения газа равна местной
Рис. 8.13. Характер изменения параметров потока вдоль сопла при πс.р > πкр
108
скорости звука, изменение давления окружающей среды не может распространяться навстречу потоку внутрь сопла и повлиять на течение газа в нем. Сопло при этом как бы заперто.
Заметим, что хотя в области πс.р > πкр скорость истечения газа из суживающегося сопла сс не может быть больше местной скорости звука,
повысить ее можно за счет увеличения температуры газа на входе в сопло Т 0* ,
так как величина скорости звука с ростом температуры газа растет.
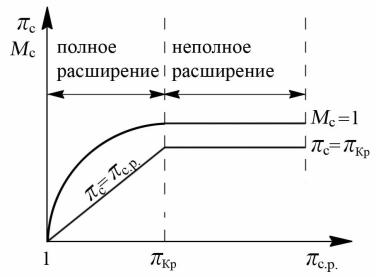
На рис. 8.14 показаны зависимости πс и числа Мс (или, что то же, скорости истечения сс) от πс.р. В области 1 < πс.р < πкр сопло работает с полным расширением газа (πс = πс.р), поэтому зависимость πс от πс.р здесь представляет собой прямую линию, выходящую из начала координат под углом 45 °. Число
Мс и соответственно скорость истечения сс с ростом πс.р увеличиваются,
достигая при πс.р = πкр критических величин (Мс = 1; сс = скр). Дальнейшее увеличение πс.р в области πс.р > πкр , как указывалось ранее,не изменяет ни πс, Мс.
На основе сказанного на рис. 8.14 можно выделить две характерные области: область полного расширения газа в сопле (1 < πс.р < πкр) и область недорасширения (при πс.р > πкр).
Рис. 8.14. Зависимости πс = f (πс.р); Мс = f (πс.р)
109
В результате недорасширения газ покидает сопло, унося с собой неиспользованную энергию. Таким образом, в режиме недорасширения не вся энергия газа используется для увеличения скорости, часть ее теряется
(рис. 8.13, б.).
8.11. Режимы работы сверхзвукового сопла (сопла Лаваля)
Сопла Лаваля применяются в тех случаях, когда необходимо получить сверхзвуковые скорости истечения. Сверхзвуковое сопло может работать на расчетном и нерасчетном режимах. В отличие от дозвукового сопла, в
сверхзвуковом сопле при определенном условии могут возникнуть два нерасчетных режима:
а) режим недорасширения (pс > pН);
б) режим перерасширения (pс < pН).
Сверхзвуковые скорости истечения могут быть достигнуты, если располагаемая степень понижения давления превосходит критическую величину. Поэтому далее будем рассматривать процесс истечения из сопла Лаваля при условии, что πс.р > πкр.
8.11.1. Изменение параметров потока вдоль сопла Лаваля
При идеальном энергоизолированном течении газа параметры потока
изменяются вдоль сопла Лаваля так, как показано на рис. 8.15.
В суживающейся части сопла поток разгоняется до скорости звука, которая достигается в критическом (минимальном) сечении сопла. Течение газа и изменение параметров потока до критического сечения сопла полностью аналогично течению в суживающемся сопле при πс.р ≥ πкр (см. рис. 8.13).
В расширяющейся части сопла происходит разгон сверхзвукового потока.
Скорость газа вдоль сопла монотонно растет, а давление и температура падают.
110
При этом в сопле Лаваля, как и в суживающемся сопле, при отсутствии трения и теплообмена со стенками температура и давление заторможенного потока будут постоянными (Т* = const, p* = const) вдоль сопла.
Важной характеристикой сопла Лаваля является относительная площадь выходного сечения (геометрическая степень расширения) сопла
|
|
Fc |
. |
|
Fc |
||||
|
||||
|
|
Fкр |
||
Из уравнения неразрывности, записанного для критического и выходного сечений, следует:
|
|
|
|
скр кр |
1 |
|
|
|
||||||
|
|
|
|
|
||||||||||
|
Fc |
|
|
|
|
|
|
|
|
. |
(8.58) |
|||
|
|
с |
|
q |
||||||||||
|
|
|
|
|
с |
|
с |
|
|
|
с |
|
||
Аналогично для произвольного сечения сопла с площадью F можно |
||||||||||||||
записать |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
F |
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
F |
|
|
|
|
. |
(8.59) |
|||||
|
|
|
F |
|
q |
|||||||||
|
|
|
|
|
|
|
кр |
|
|
|
|
|
|
|
При заданной величине показателя адиабаты k существует однозначная связь (см. вопрос 8.8) между относительной плотностью тока q (λ) и
остальными газодинамическими функциями М, λ, τ(λ), π(λ), ε(λ),
определяющими при заданных значениях p1* и T1* параметры потока в рассматриваемом произвольном сечении сопла. Таким образом, если известен закон профилирования сопла Лаваля, то есть изменение площади проходных сечений по длине сопла, то это позволяет определить изменение относительной плотности тока q(λ) и остальных газодинамических функций, а соответственно и всех параметров потока вдоль сопла.
На рис. 8.16 показано изменение относительной плотности тока q(λ) в сопле Лаваля. В критическом сечении относительная плотность тока достигает максимального значения q(λкр) = 1, а в суживающейся и расширяющейся частях сопла q(λ) снижается при увеличении F.
