Осень 13-весна 14 курс 1-2 ОрТОР (сейчас это называют ТОЛААД) / Физика / Решебники / Fizika._Praktikum._Chast_1

Кинематика

1.1. Две прямые дороги пересекаются под углом α = 60,0°. От перекрестка по ним удаляются машины: одна со скоростью υ1 = 60,0 км/ч, другая со скоростью υ2 = 80,0 км/ч. Определите скорости υотн, с которыми одна машина удаляется от другой. Перекресток машины прошли одновременно. Рассмотреть два возможных варианта.

средняя путевая скорость υ 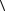автомобиля?

1.3. Тело прошло первую половину пути со скоростью υ1 = 4,0 м/с. На оставшейся части пути оно половину времени двигалось со скоростью υ2 = 3,0 м/с, а последний участок прошло со скоростью υ3 = 6,0 м/с. Определите среднюю путевую скорость υ тела.

1.4. Движение материальной точки задано уравнением х = Аt + Bt2, где А = 4,0 м/с, B = – 0,050 м/с2. Определите момент времени t, в который скорость υ точки равна нулю. Найдите координату x и проекцию ускорения ax в этот момент. Постройте графики зависимости координаты, пути, проекции скорости и проекции ускорения этого движения от времени.

1.5. Из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через τ = 2,00 с после первой. Первая точка двигалась с начальной скоростью υ1 = 1,00 м/с и ускорением a1 = 2,00 м/с2, вторая – с начальной скоростью υ2 = 10,0 м/с и ускорением a2 = 1,00 м/с2. Через какое время t и на каком расстоянии l от исходного положения вторая точка догонит первую?

1.6. Две материальные точки движутся согласно уравнениям

x1=A1t + B1t2 + C1 t3, x2=A2t + B2t2 + C2t3, где A1 = 4,00 м/с, B1 = 8,00 м/с2,

C1 = – 16,0 м/с3, А2 = 2,00 м/с, В2 = – 4,00 м/с2, С2 = 1,00 м/с3.

В какой момент времени t ускорения этих точек будут одинаковы? Найдите проекции скоростей υ1x и υ2x точек в этот момент.

1.7. При экстренном торможении скорость автомобиля начинает из-

меняться по закону υ = Ae−bt − B , где А = 100 м/с, В = 80,0 м/с, коэффициент пропорциональности b = 0,100 с–1 . Найдите t время движения автомобиля до остановки, максимальное amax и минимальное amin значения уско-

84

рения в процессе торможения. Определите зависимость a(υ) ускорения от скорости и постройте соответствующий график.

1.8. Камень падает с высоты h = 1200 м. Какой путь l пройдет камень за последнюю секунду своего падения?

1.9. Камень брошен вертикально вверх с начальной скоростью υ0 = 20,0 м/с. По истечении какого времени t камень будет находиться на высоте h = 15,0 м? Найдите скорость υ камня на этой высоте. Сопротивлением воздуха пренебречь.

1.10. Тело, брошенное вертикально вверх, находилось на одной и той же высоте h = 8,60 м два раза с интервалом ∆t = 3,00 с. Пренебрегая сопротивлением воздуха, вычислите начальную скорость υ0 брошенного тела.

1.11. Тело брошено с балкона вертикально вверх со скоростью υ0 = 10,0 м/с. Высота балкона над поверхностью земли h = 12,5 м. Напишите уравнение движения и определите среднюю путевую скорость υ с момента бросания до момента падения на землю.

1.12.Движение точки по прямой задано уравнением х = Аt + Вt2, где

А= 2,0 м/с, В = – 0,50 м/с2. Определите среднюю путевую скорость υ

движения точки в интервале времени от t1 = 1,0 с до t2 = 3,0 с.

1.13. Материальная точка движется по плоскости согласно уравнению

1.15. Точка движется по кривой с постоянным тангенциальным ускорением aτ = 0,500 м/с2. Определите полное ускорение a точки на участке кривой с радиусом кривизны R = 3,00 м, если точка движется на этом участке со скоростью υ = 2,00 м/с.

1.16. По окружности радиусом R = 5,0 м равномерно движется материальная точка со скоростью υ = 5,0 м/с. Постройте графики зависимости

85

1.17. За время t = 6,00 с точка прошла путь, равный половине длины окружности радиусом R = 80,0 см. Определите среднюю путевую скорость

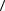υ за это время и модуль вектора средней скорости υR .

1.18.Точка движется по окружности радиусом R = 2,00 м согласно уравнению ξ=Аt3, где А = 2,00 м/с3. В какой момент времени t нормальное

ускорение аn точки будет равно тангенциальному aτ? Определите полное ускорение а в этот момент.

1.19.Материальная точка движется по окружности радиусом R = 1,0 м согласно уравнению l = 8,0t – 0,20 t3, м. Найдите скорость υ, тангенциальное aτ, нормальное an и полное a ускорение в момент времени t = 2,0 с.

1.20.Определите скорость υ и полное ускорение a точки в момент времени t = 2,00 с, если она движется по окружности радиусом R = 1,00 м согласно уравнению ξ = At + Bt3, где А = 8,00 м/с; В = – 1,00 м/с3; ξ – криволинейная координата, отсчитанная вдоль окружности от некоторой точки, принятой за начальную.

1.21.Точка обращается по окружности радиусом R = 1,20 м. Уравнение движения точки φ = At + Bt3, где А = 0,500 рад/с; В = 0,200 рад/с3. Определите тангенциальное aτ, нормальное an и полное a ускорения точки

вмомент времени t = 4,00 с.

1.22.Движение точки по кривой задано уравнениями х = А1t3 и у = A2t, где А1 = 1,00 м/с3, А2 = 2,00 м/с. Найдите уравнение траектории точки, ее

скорость υ и полное ускорение а в момент времени t = 0,800 c.

1.23. С вышки бросили камень в горизонтальном направлении. Через промежуток времени t = 2,00 с камень упал на землю на расстоянии l = 40,0 м от основания вышки. Определите начальную υ0 и конечную υ скорости камня.

1.24. Пистолетная пуля пробила два вертикально закрепленных листа бумаги, расстояние между которыми l = 30,0 м. Пробоина во втором листе оказалась на h = 10,0 см ниже, чем в первом. Определите скорость υ пули,

86

если к первому листу она подлетела, двигаясь горизонтально. Сопротивлением воздуха пренебречь.

1.25.Пуля пущена с начальной скоростью υ0 = 200 м/с под углом

α= 60,0° к горизонту. Определите максимальную высоту Н подъема, дальность l полета и радиус R кривизны траектории пули в ее наивысшей точке. Сопротивлением воздуха пренебречь.

1.26.Тело брошено под углом α = 30° к горизонту. Найдите тангенциальное aτ и нормальное аn ускорения в начальный момент движения.

1.27.На цилиндр, который может вращаться вокруг горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему

возможность опускаться. Двигаясь равноускоренно, грузик за время t = 3,00 с опустился на h = 1,50 м. Определите угловое ускорение ε цилиндра, если его радиус R = 4,00 см.

1.28.Маховик начал вращаться равноускоренно и за промежуток времени ∆t = 10,0 с достиг частоты вращения п = 300 мин–1 . Определите угловое ускорение ε маховика и число N оборотов, которое он сделал за это время.

1.29.Велосипедное колесо вращается с частотой п = 5,00 с–1 . Под действием сил трения оно остановилось через интервал времени ∆t = 1,00 мин. Определите угловое ускорение ε и число N оборотов, которое сделает колесо за это время.

1.30.Колесо автомашины вращается равноускоренно. Сделав N = 50,0

полных оборотов, оно изменило частоту вращения от п1 = 4,00 с–1 до n2 = 6,00 с–1 . Определите угловое ускорение ε колеса.

Динамика материальной точки

ипоступательного движения твердого тела

1.31.К пружинным весам подвешен блок. Через блок перекинут шнур,

кконцам которого привязали грузы массами m1= 1,50 кг и m2 = 3,00 кг. Каково будет показание P весов во время движения грузов? Массой блока и шнура пренебречь.

87

1.32.Шайба, пущенная по поверхности льда с начальной скоростью

υ0 = 20 м/с, остановилась через t = 40 с. Найдите коэффициент трения µ шайбы о лед.

1.33.Диск радиусом R = 40 см вращается вокруг вертикальной оси. На краю диска лежит кубик. Принимая коэффициент трения µ = 0,40, найдите частоту n вращения, при которой кубик соскользнет с диска.

1.34.Грузик, привязанный к шнуру длиной l = 50 см, описывает окружность в горизонтальной плоскости. Какой угол α образует шнур с вертикалью, если частота вращения п = 1,0 с–1 ?

1.35.Мотоцикл едет по внутренней поверхности вертикального цилиндра радиусом R = 11,2 м. Центр тяжести мотоцикла с человеком расположен на расстоянии l = 0,800 м от поверхности цилиндра. Коэффициент трения покрышек о поверхность цилиндра µ = 0,600. С какой минимальной

скоростью υmin должен ехать мотоциклист? Каков будет при этом угол α наклона его к плоскости горизонта?

1.36. Автомобиль едет по закруглению шоссе с радиусом кривизны R = 200 м. Коэффициент трения колес о покрытие дороги µ = 0,100 (гололед). При какой скорости υ автомобиля начнется его занос?

1.37.Тело массой т = 5,00 кг брошено под углом α = 30,0° к горизонту с начальной скоростью υ0 = 20,0 м/с. Пренебрегая сопротивлением воздуха, найдите: 1) импульс силы F t, действующей на тело, за время его полета; 2) приращение ∆p импульса тела за время полета.

1.38.Шарик массой т = 100 г упал с высоты h = 2,50 м на горизонтальную плиту, масса которой много больше массой шарика, и отскочил от нее вверх. Считая удар абсолютно упругим, определите импульс p, полученный плитой.

1.39. Шарик массой m = 100 г ударился о стенку со скоростью υ = 5,00 м/с и отскочил от нее с той же скоростью. Определите импульс p, полученный стенкой, если до удара шарик двигался под углом α = 60,0o к плоскости стенки.

1.40. Ракета массой т = 1,00 т, запущенная с поверхности Земли вертикально вверх, поднимается с ускорением а = 2g. Скорость струи газов,

88

вырывающихся из сопла, равна υ = 1200 м/с. Найдите массовый расход Qm горючего.

1.41.Космический корабль имеет массу т = 3,50 т. При маневрировании из его двигателей вырывается струя газов со скоростью υ = 800 м/с;

расход горючего Qm = 0,2 кг/с. Найдите реактивную силу Fр двигателей и ускорение а, которое она сообщает кораблю.

1.42.Вертолет массой т = 3,50 т с ротором, диаметр d которого равен 18 м, «висит» в воздухе. С какой скоростью υ ротор отбрасывает вертикально вниз струю воздуха? Диаметр струи считать равным диаметру ротора.

1.43.Какую силу F надо приложить к вагону, стоящему на рельсах, чтобы вагон стал двигаться равноускоренно и за время t = 30 с прошел путь l = 11 м? Масса вагона m = 16 т. Во время движения на вагон действует сила трения, равная n = 0,050 веса вагона.

1.44.Тело лежит на наклонной плоскости, составляющей с горизонтом угол α = 4,00°. 1) При каком предельном значении коэффициента трения

μmax тело начнет скользить по наклонной плоскости? 2) С каким ускорением a будет скользить тело по плоскости, если коэффициент трения равен

μ= 0,0300? 3) Какое время t потребуется для прохождения при этих условиях l = 100 м пути? 4) Какую скорость υ тело будет иметь в конце этого участка?

1.45.На какую высоту h поднимется тело, скользя вверх по наклонной

плоскости с углом наклона α = 45°, если ему сообщить скорость υ0 = 10,0 м/с, а коэффициент трения между телом и плоскостью μ = 0,200? Какова будет скорость υ тела, когда оно вернется в нижнюю точку?

1.46.Спускаясь при выключенном двигателе с горы, имеющей уклон

α= 5,7°, автомобиль движется равномерно. Какова должна быть сила Fт тяги двигателя автомобиля, чтобы он мог подниматься в такую же гору с той же скоростью? Масса автомобиля т = 1,0 т. Силу сопротивления движению в обоих случаях считать одинаковой.

1.47.Бак в тендере паровоза имеет длину l = 4,00 м. Какова разность ∆h уровней воды у переднего и заднего концов бака при движении поезда с ускорением а = 0,500 м/с2?

89

1.48. Струя воды ударяется о неподвижную плоскость, поставленную под углом φ = 60° к направлению движения струи. Скорость струи υ = 20,0 м/с, площадь ее поперечного сечения S = 5,00 см2. Определите силу F давления струи на плоскость.

1.49. Какой наибольший груз может выдержать стальная проволока диаметром d = 1,00 мм, не выходя за предел упругости σупр = 294 МПа? Какую долю ε первоначальной длины составляет удлинение проволоки при этом грузе?

1.50.Однородный стержень длиной l = 1,20 м, площадью поперечного сечения S = 2,00 см2 и массой т = 10,0 кг вращается с частотой п = 2,00 с–1 вокруг вертикальной оси, проходящей через конец стержня, скользя при этом без трения по горизонтальной поверхности. Найдите наибольшее напряжение σmах материала стержня при данной частоте вращения.

1.51.К вертикальной проволоке длиной l = 5,00 м и площадью поперечного сечения S = 2,00 мм2 подвешен груз массой т = 5,10 кг. В результате проволока удлинилась на х = 0,600 мм. Найдите модуль Юнга E материала проволоки.

1.52.Проволока длиной l = 2,0 м и диаметром d = 1,0 мм натянута практически горизонтально. Когда к середине проволоки подвесили груз массой m = 1,0 кг, проволока растянулась настолько, что точка подвеса опустилась на h = 4,0 см. Определите модуль Юнга E материала проволоки.

1.53.Две пружины жесткостями k1 = 0,30 кН/м и k2 = 0,80 кН/м соединены последовательно. Определите абсолютную деформацию х1 первой пружины, если вторая деформирована на x2 = 1,5 см.

1.54.Снаряд массой т = 10,0 кг выпущен из зенитного орудия верти-

кально вверх со скоростью υ0 = 800 м/с. Считая силу сопротивления воздуха пропорциональной скорости, определите время t подъема снаряда до высшей точки. Коэффициент сопротивления k = 0,250 кг/с.

1.55.С вертолета, неподвижно висящего на некоторой высоте над поверхностью Земли, сброшен груз массой т = 100 кг. Считая, что сила сопротивления воздуха изменяется пропорционально скорости, определите,

через какой промежуток времени τ ускорение а груза будет равно поло-

90

вине ускорения свободного падения. Коэффициент сопротивления

k= 10,0 кг/с.

1.56.Моторная лодка массой т = 400 кг начинает двигаться по озеру. Сила тяги мотора равна F = 200 Н. Считая силу сопротивления Fc пропор-

циональной скорости, определите скорость υ лодки через τ = 20,0 с после начала ее движения. Коэффициент сопротивления k = 20,0 кг/с.

1.57. Катер массой т = 2,00 т трогается с места и в течение времени τ = 10,0 с развивает при движении по спокойной воде скорость υ = 4,00 м/с. Определите силу тяги F мотора, считая ее постоянной. Принять силу сопротивления Fс движению пропорциональной скорости; коэффициент сопротивления k = 100 кг/с.

1.58. Моторная лодка массой т = 200 кг, достигнув скорости υ = 8,00 м/с, далее стала двигаться с выключенным двигателем. Считая силу сопротивления пропорциональной скорости, определите путь l, пройденный лодкой за время τ с момента выключения двигателя. Коэффициент сопротивления принять равным k = 25,0 кг/с.

1.59.Парашютист, масса которого т = 80 кг, совершает затяжной прыжок. Считая, что сила сопротивления воздуха пропорциональна скорости, определите, через какой промежуток времени τ скорость движения парашютиста будет равна 0,9 от скорости установившегося движения. Коэффициент сопротивления k = 10 кг/с. Начальная скорость парашютиста равна нулю.

1.60.Метеорит массой m = 1,00 кг, влетевший в верхние слои атмосферы со скоростью υ0 = 3,00 км/с, начинает испытывать силу сопротивле-

ния, пропорциональную квадрату скорости Fс = kυ 2 , где k = 1,00×10–3 кг/м.

Какой путь l пролетит метеорит в атмосфере к моменту, когда его скорость уменьшится вдвое.

Силы тяготения. Гравитационное поле

1.61. Радиус планеты Марс равен R = 3,4×106 м, ее масса М = 6,4·1023 кг. Определите напряженность g гравитационного поля на поверхности Марса.

91

1.62.Радиус Земли в n = 3,66 раза больше радиуса Луны; средняя плотность Земли в k = 1,66 раза больше средней плотности Луны. Опреде-

лите ускорение свободного падения gЛ на поверхности Луны, если на поверхности Земли ускорение свободного падения g считать известным.

1.63.Искусственный спутник обращается вокруг Земли по окружности на высоте h = 3,6·106 м. Определите линейную скорость υ спутника. Радиус R Земли и ускорение свободного падения g на поверхности Земли считать известными.

1.64.Период вращения искусственного спутника Земли T = 2,00 ч. Считая орбиту спутника круговой, найдите, на какой высоте h над поверхностью Земли движется спутник.

1.65.Планета Нептун в k = 30 раз дальше от Солнца, чем Земля. Определите период T обращения (в годах) Нептуна вокруг Солнца.

1.66.Луна движется вокруг Земли со скоростью υ1 = 1,02 км/с. Среднее расстояние l Луны от Земли равно 60,3R (R – радиус Земли). Определи-

те по этим данным, с какой скоростью υ2 должен двигаться искусственный спутник, вращающийся вокруг Земли на незначительной высоте над ее поверхностью.

1.67.Зная среднюю скорость υ1 движения Земли вокруг Солнца (30,0 км/с), определите, с какой средней скоростью υ2 движется малая планета, радиус орбиты которой в n = 4,0 раза больше радиуса орбиты Земли.

1.68.Космическая ракета, ставшая искусственной планетой, обраща-

ется вокруг Солнца по эллипсу. Наименьшее расстояние rmin ракеты от Солнца равно 0,97 а.е., наибольшее расстояние rmax равно 1,31 а.е. (среднего расстояния Земли от Солнца). Определите период T вращения (в годах) искусственной планеты.

1.69.Космическая ракета движется вокруг Солнца по орбите, почти совпадающей с орбитой Земли. При включении тормозного устройства ракета быстро теряет скорость и начинает падать на Солнце (рис. 23). Определите время t, в течение которого будет падать ракета.

Указание. Принять, что, падая на Солнце, ракета движется по эллипсу, большая ось которого очень мало отличается от радиуса орбиты Земли, а эксцентриситет — от единицы. Период обращения по эллипсу не зависит от эксцентриситета.

92