
Осень 13-весна 14 курс 1-2 ОрТОР (сейчас это называют ТОЛААД) / Физика / Решебники / Fizika._Praktikum._Chast_1
.pdf
ления Больцмана, найдите объем V0 частиц, если при расстоянии между двумя слоями h = 80 мкм число взвешенных частиц в одном слое вдвое больше, чем в другом. Плотность краски ρ = 1700 кг/м3, а температура окружающей среды Т = 300 К.
2.26. Ротор центрифуги вращается с угловой скоростью ω. Используя функцию распределения Больцмана, установите распределение концентрации n частиц массой m, находящихся в роторе центрифуги, как функцию расстояния r от оси вращения.
2.27. В центрифуге находится некоторый газ при температуре Т = 271 К. Ротор центрифуги радиусом r = 0,400 м вращается с угловой скоростью ω = 500 рад/с. Определите относительную молекулярную массу Мr газа, если давление p у стенки ротора в 2,10 раза больше давления р0 в его центре.
2.28.Ротор центрифуги, заполненный радоном, вращается с частотой n = 50,0 с–1 . Радиус ротора r = 0,500 м. Определите давление p газа на стен-
ки ротора, если в его центре давление р0 равно нормальному атмосферному. Температуру T по всему объему считать одинаковой и равной 300 К.
2.29.Зная функцию распределения молекул по скоростям, выведите формулу наиболее вероятной скорости υв.
2.30.Используя функцию распределения молекул по скоростям, получите функцию, выражающую распределение молекул по относительным
скоростям u (u = υ/ υв).
Явления переноса
2.31.Найдите среднее время  τ
τ свободного пробега молекул кислорода при температуре Т = 250 К и давлении p = 100 Па.
свободного пробега молекул кислорода при температуре Т = 250 К и давлении p = 100 Па.
2.32.Найдите зависимость средней длины  l
l  свободного пробега
свободного пробега
молекул идеального газа от давления р при следующих процессах: 1) изотермическом; 2) изохорном. Изобразите эти зависимости на графиках.
2.33. Найдите зависимость среднего числа столкновений молекул идеального газа в 1 с от температуры T при следующих процессах: 1) изобарном; 2) изохорном. Изобразите эти зависимости на графиках.
113

2.34. Коэффициент диффузии D кислорода при температуре t = 0 ° С равна 0,190 см2/с. Определите среднюю длину  l
l  свободного пробега молекул кислорода.
свободного пробега молекул кислорода.
2.35.Определите зависимость коэффициента диффузии D от температуры T при следующих процессах: 1) изобарном; 2) изохорном. Изобразите эти зависимости на графиках.
2.36.Определите зависимость коэффициента диффузии D от давления р при следующих процессах: 1) изотермическом; 2) изохорном. Изобразите эти зависимости на графиках.
2.37.Найдите среднюю длину 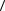 l
l  свободного пробега молекул азота при условии, что его динамическая вязкость η = 17,0 мкПа·с.
свободного пробега молекул азота при условии, что его динамическая вязкость η = 17,0 мкПа·с.
2.38.Определите зависимость динамической вязкости η от температуры T при следующих процессах: 1) изобарном; 2) изохорном. Изобразите эти зависимости на графиках.
2.39.Самолет летит со скоростью υ = 360 км/ч. Считая, что слой воздуха у крыла самолета, увлекаемый вследствие вязкости, h = 4,00 см,
найдите касательную силу FS, действующую на единицу поверхности крыла. Диаметр молекул воздуха d = 0,3 нм. Температура воздуха t = 0 ° С.
2.40.Цилиндр радиусом R1 = 10 см и длиной l = 30 см расположен внутри цилиндра радиусом R2 = 10,5 см так, что оси обоих цилиндров совпадают. Малый цилиндр неподвижен, большой вращается относительно геометрической оси с частотой n = 15 с–1 . Динамическая вязкость η газа, в котором находятся цилиндры, равна 8,5 мкПа·с. Определите: 1) касатель-
ную силу Fτ, действующую на поверхность внутреннего цилиндра площадью S = 1,0 м2; 2) вращающий момент М, действующий на этот цилиндр.
2.41.Два горизонтальных диска радиусомми R = 20,0 см расположены друг над другом так, что оси их совпадают. Расстояние d между плоскостями дисков равно 5,00 мм. Верхний диск неподвижен, нижний вращается относительно геометрической оси с частотой n = 10,0 с–1 . Найдите вращающий момент М, действующий на верхний диск. Динамическая вязкость η воздуха, в котором находятся диски, равна 17,2 мкПа·с.
114
2.42. Определите массу m азота прошедшего вследствие диффузии через площадку S = 50,0 см2 за время t = 20,0 с, если градиент плотности в направлении, перпендикулярном площадке, равен 1,00 кг/м4. Температура азота Т = 290 К, а средняя длина свободного пробега его молекул равна 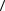 l
l  = 1,00 мкм.
= 1,00 мкм.
2.43. Пространство между двумя большими параллельными пластинами, расстояние d между которыми равно 5,00 мм, заполнено гелием. Температура Т1 одной пластины поддерживается равной 290 К, а другой – Т2 = 310 К. Вычислите плотность теплового потока |q|. Расчеты выполните для двух случаев, когда давление p гелия равно: 1) 0,100 МПа; 2) 1,00 мПа.
2.44. Какое количество |
теплоты Q теряет помещение за время |
t = 1,00 ч через окно за счет |
теплопроводности воздуха, заключенного |
между рамами? Площадь каждой рамы S = 4,00 м2, расстояние между ними l = 30,0 см. Температура помещения t1 = 18,0 ° С, температура наружного воздуха t2 = −20 °C . Диаметр молекул воздуха d = 0,300 нм. Температуру
воздуха между рамами считать равной среднему арифметическому температур помещения и наружного воздуха. Давление р = 101,3 кПа.
2.45. Между двумя пластинами, находящимися на расстоянии l = 1,00 мм друг от друга, находится воздух. Между пластинами поддерживается разность температур ∆Т = 1,00 К. Площадь каждой пластины S = 100 см2. Какое количество теплоты Q передается за счет теплопроводности от одной пластины к другой за время t = 10,0 мин? Считать, что воздух находится при нормальных условиях. Диаметр молекул воздуха d = 0,300 нм.
Теплоемкость идеальных газов. Первый закон термодинамики
2.46.Определите показатель адиабаты γ для смеси газов, содержащей гелий массой m1 = 8,0 г и водород массой m2 = 2,0 г.
2.47.Разность удельных теплоемкостей ср – сV некоторого двух атомного газа равна 260 Дж/(кг·К). Найдите молярную массу М газа и его удельные теплоемкости сV и ср.
2.48.Во сколько раз молярная теплоемкость Сm1 гремучего газа больше молярной теплоемкости Сm2 водяного пара, получившегося при его сгорании? Задачу решить для: 1) V = const; 2) р = const.
115
2.49.Каковы удельные теплоемкости сV и ср смеси газов, содержащей кислород массой m1 = 10 г и азот массой m2 = 20 г?
2.50.Найдите удельную теплоемкость ср газовой смеси, состоящей из количества ν1 = 3,00 моль аргона и количества ν2 = 2,00 моль азота.
2.51.Определите удельную теплоемкость сV смеси газов, содержащей V1 = 5,00 л водорода и V2 = 3,00 л гелия. Газы находятся при одинаковых условиях.
2.52.В баллоне находится аргон и азот. Определите удельную тепло-
емкость сV смеси этих газов, если массовые доли аргона (w1) и азота (w2) одинаковы и равны w = 0,500.
2.53.Удельная теплоемкость газовой смеси, состоящей из количества
ν1 |
= 1,00 моль кислорода и некоторой массы m2 аргона, равна |
ср |
= 430 Дж/(кг·К). Какая масса m2 аргона находится в газовой смеси? |
2.54.Смесь газов состоит из аргона и азота, взятых при одинаковых условиях и в одинаковых объемах. Определите показатель адиабаты γ такой смеси.
2.55.Определите удельные теплоемкости сV и ср смеси углекислого газа массой m1 = 3,00 г и азота массой m2 = 4,00 г.
2.56.Кислород массой m = 2,0 кг занимает объем V1 = 1,0 м3 и находится под давлением р1 = 0,20 МПа. Газ был нагрет сначала при постоянном давлении до объема V2 = 3,0 м3, а затем при постоянном объеме до
давления р2 = 0,50 МПа. Найдите: 1) приращение DU внутренней энергии газа; 2) совершенную им работу A; 3) количество теплоты Q, переданную газу. Постройте график процесса в координатах p-V.
2.57.При изотермическом расширении водорода массой m = 2,0 кг,
взятого при давлении р1 = 6,0×105 Па и объеме V1 = 8,31 м3, была совершена работа A = 5,47 МДж. После изотермического расширения газ был адиабатно сжат до первоначального объема. Определите, в каком случае была совершена большая по модулю работа и во сколько раз. Постройте график процесса в координатах p-V.
2.58.При температуре Т1 = 300 К и давлении р1 = 2,0×105 Па углекислый газ массой m = 4,4 кг адиабатно был сжат до некоторого давления р2,
116
при этом объем уменьшился в два раза. После сжатия газ изобарно расширился до первоначального объема. Определите: 1) приращение DU внутренней энергии газа; 2) количество теплоты Q, подведенное к газу; 3) работу A совершенную газом. Постройте график процесса в координатах p-V.
2.59.При расширении кислорода массой m = 10 г объем его увеличился в 10 раз. Найдите, во сколько раз и в каком случае газ совершит большую работу A, если он будет расширятся адиабатно или изотермически. Постройте график процесса в координатах p-V.
2.60.Водород массой m = 40 г, имевший температуру Т1 = 300 К, изобарно расширился, увеличив объем в n1 = 3 раза. Затем при изотермическом сжатии объем газа уменьшился в n2 = 2 раза. Определите: 1) пол-
ную работу A, совершенную газом; 2) приращение DU внутренней энергии; 3) количество теплоты Q полученное газом. Постройте график процесса в координатах p-V.
2.61. Некоторая масса азота при давлении р1 = 1,0×105 Па имела объем V1 = 5,0 л, а при давлении р3 = 3,0×105 Па объем V3 = 2,0 л. Переход от одного состояния к другому произведен в два этапа: сначала по изохоре, а затем по адиабате. Определите: 1) приращение DU внутренней энергии; 2) количество теплоты Q полученное газом; 3) работу А совершенную газом. Постройте график процесса в координатах p-V.
2.62. |
В цилиндре под |
поршнем |
находится водород массой |
m = 0,020 кг |
при температуре |
Т1 = 300 К. |
Водород сначала расширился |
адиабатно, увеличив свой объем в пять раз, а затем был сжат изотермически, причем объем газа уменьшился в пять раз. Найдите температуру Т2 в конце адиабатного расширения и полную работу A, совершенную газом. Постройте график процесса в координатах p-V.
2.63. Азот массой m = 50 г находится при температуре Т1 = 280 К. В результате изохорного охлаждения его давление уменьшилось в n = 2 раза, а затем в результате изобарного расширения температура газа в конечном состоянии стала равной первоначальной. Определите: 1) работу A, совершенную газом; 2) приращение DU внутренней энергии газа. Постройте график процесса в координатах p-V.
2.64. Кислород массой m = 10 г, находящийся при температуре Т1 = 370 К, подвергли адиабатному расширению, в результате которого его давление уменьшилось в n = 4,0 раза. В результате последующего изотер-
117
мического процесса газ сжимается до первоначального давления. Определите: 1) температуру Т3 в конце процесса; 2) количество теплоты Q, отданное газом; 3) приращение DU внутренней энергии газа; 4) работу A, совершенную газом. Постройте график процесса в координатах p-V.
2.65. При температуре t1 = 17 ° С и давлении р1 = 2,0×105 Па оксид углерода (СО2) массой m = 4,4 кг адиабатно был сжат до некоторого давления р2. После сжатия газ изотермически расширился. Определите параметры газа после расширения, если приращение внутренней энергии в адиабатном процессе ∆U = 108 кДж равно количеству теплоты Q, сообщенному в изотермическом процессе. Постройте график процесса в координатах p-V.
Круговые процессы. Энтропия
2.66.Идеальный двухатомный газ, содержащий количество вещества
ν= 1,0 моль, совершает цикл, состоящий из двух изохор и двух изобар.
Наименьший объем Vmin = 10 л, наибольший Vmax = 20 л, наименьшее давление pmin = 246 кПа, наибольшее рmax = 410 кПа. Постройте график цикла в координатах p-V. Определите температуру T газа для характерных точек цикла и его КПД η цикла.
2.67.Идеальный двухатомный газ совершает цикл Карно, в процессе
адиабатного расширения объем газа увеличивается от V1 = 12 л до V2 = 16 л. Найдите КПД η цикла.
2.68.Идеальный двухатомный газ, содержащий количество вещества
ν= 1,0 моль, совершает замкнутый цикл, состоящий из двух изохор и двух
изобар. Наименьший |
объем Vmin = 2,0 м3, наибольший Vmax = 3,0 м3, |
наименьшее давление |
pmin = 1,2 МПа, наибольшее рmax = 1,6 МПа. По- |
стройте график цикла в координатах p-V. Определите: 1) количество теплоты Q1, полученное от нагревателя; 2) количество теплоты Q2, переданное охладителю; 3) работу A, совершаемую газом за цикл; 4) КПД η цикла.
2.69. Идеальный газ, совершающий цикл Карно, 70 % количества теплоты Q1, полученной от нагревателя, отдает охладителю. Количество теплоты Q1, полученное от нагревателя, равно 5,0 кДж. Определите:
1)КПД η цикла; 2) работу A, совершенную при полном цикле.
2.70.Идеальный многоатомный газ совершает цикл, состоящий из двух изохор и двух изобар, причем наибольшее давление газа в два раза
118
больше наименьшего, а наибольший объем в четыре раза больше наименьшего. Определите КПД η цикла.
2.71. Идеальная тепловая машина работает по циклу Карно. Воздух
при давлении p1 = 1,0 МПа и температуре t1 = 127 ° С занимает |
объем |
||
V1 |
= 2,0 л. |
После изотермического расширения воздух занял |
объем |
V2 |
= 5,0 л, |
после адиабатного расширения объем стал равным V3 = 8,0 л. |
|
Найдите: 1) координаты пересечения изотерм и адиабат; 2) работу А, совершаемую на каждом участке цикла; 3) полную работу АΣ, совершаемую за весь цикл; 4) КПД η цикла; 5) количество теплоты Q1, полученное от нагревателя за один цикл; 6) количество теплоты Q2, переданное охладителю за один цикл.
2.72. Азот |
массой |
m = 500 г, находящийся |
под давлением |
|
p1 = 1,00 МПа |
при температуре t1 = 127 ° С, подвергли |
изотермическому |
||
расширению, |
в |
результате |
которого давление газа |
уменьшилось в |
n = 3,00 раза. После этого газ подвергли адиабатному сжатию до начального давления, а затем он был изобарно сжат до начального объема. Постройте график цикла в координатах p-V. Определите работу A, совершенную газом за цикл.
2.73. Одноатомный газ, содержащий количество вещества ν = 0,100 моль, под давлением p1 = 100 кПа занимал объем V1 = 5,00 л. Газ сжимался изобарно до объема V2 = 1,00 л, затем сжимался адиабатно и расширялся при постоянной температуре до начального объема и давления. Постройте график цикла в координатах p-V. Найдите: 1) температуры Т1, Т2, объемы V2, V3 и давление р3, соответствующее характерным точкам цикла; 2) количество теплоты Q1, полученное от нагревателя; 3) количество теплоты Q2, переданное охладителю; 4) работу A, совершаемую газом за весь цикл; 4) КПД η цикла.
2.74. Количество ν = 1,00 моль идеального газа совершает цикл, состоящий из двух изохор и двух изобар. При этом объем газа изменяется от V1 = 25,0 л до V2 = 50,0 л и давление изменяется от p1 = 100 кПа до p2 = 200 кПа. Во сколько раз работа, совершаемая при таком цикле, меньше работы, совершаемой в цикле Карно, изотермы которого соответствуют наибольшей и наименьшей температурам рассматриваемого цикла, если при изотермическом расширении объем увеличился в 2,00 раза?
2.75. Наименьший объем V1 газа, совершающего цикл Карно, равен 153 л. Определите наибольший объем V3, если объем V2 в конце изотерми-
119
ческого расширения и объем V4 в конце изотермического сжатия равны соответственно 600 и 189 л.
2.76.Идеальный двухатомный газ, занимающий объем V1 = 2,00 л, подвергают адиабатному расширению, в результате которого его объем возрос в n = 5,00 раз. После этого газ подвергли изобарному сжатию до первоначального объема, а затем он в результате изохорного нагревания возвращен в первоначальное состояние. Постройте график цикла в координатах p-V. Определите КПД η цикла.
2.77.Идеальный газ совершает цикл Карно. Температура нагревателя
Т1 = 500 К, охладителя Т2 = 300 К. Работа А изотермического расширения составляет 2,00 кДж. Определите: 1) КПД η цикла; 2) количество теплоты Q2, отданное газом при изотермическом сжатии охладителю.
2.78.Идеальный двухатомный газ (ν = 3,00 моль), занимающий объ-
ем V1 = 5,00 л и находящийся под давлением p1 = 1,00 МПа, подвергают изохорному нагреванию до Т2 = 500 К. После этого газ подвергли изотермическому расширению до начального давления, а затем он в результате изобарного сжатия возвращен в первоначальное состояние. Постройте график цикла в координатах p-V. Определите КПД η цикла.
2.79.Найдите приращение DS энтропии алюминиевого бруска массой m = 3,0 кг, если он нагревается от Т1 = 300 К до Т2 = 940 К и плавится.
Вэтом интервале температур удельная теплоемкость алюминия c = a + bT ,
где а = 0,77 Дж/(г×К), b = 0,46 Дж/(г×К2). Удельная теплота плавления алюминия l = 322 кДж/кг.
2.80.При нагревании n = 1,0 моль двухатомного газа его абсолютная температура увеличивается в 1,5 раза. Найдите приращение DS энтропии, если нагревание происходит: 1) изохорно; 2) изобарно.
2.81.Найдите приращение DS энтропии n = 2,00 моль идеального газа с показателем адиабаты g = 1,30, если в результате некоторого процесса объем газа увеличился в два раза, а давление уменьшилось в 3 раза.
2.82.Кусок меди массой m1 = 300 г при температуре t1 = 97,0 °C поместили в калориметр, где находится вода массой m2 = 100 г при темпера-
туре t2 = 7,0 °C. Найдите приращение DS энтропии системы к моменту установления теплового равновесия. Удельные теплоемкости меди и воды
120
соответственно равны с1 = 395 Дж/(кг×К) и с2 = 4,20 кДж/(кг×К). Теплоемкость калориметра пренебрежимо мала.
2.83. Смешали воду массой m1 = 5,0 кг при температуре Т1 = 280 К с водой массой m2 = 8,0 кг при температуре Т1 = 350 К. Найдите: 1) температуру q смеси; 2) приращение DS энтропии, происходящее при смешивании. Удельная теплоемкость воды с = 4200 Дж/(кг×К).
2.84. Кусок льда массой m = 200 г, взятый при температуре t1 = −10 °C , был нагрет до температуры t2 = 0 °C и расплавлен, после чего
образовавшаяся вода была нагрета до температуры t3 = 10 °C. Определите приращение DS энтропии в ходе указанных процессов. Удельные теплоемкости льда и воды соответственно равны с1 = 2,10 кДж/(кг×К) и с2 = 4,20 кДж/(кг×К). Удельная теплота плавления льда l1 = 3,35×105 Дж/кг.
2.85. Водород массой m = 100 г был изобарно нагрет так, что его объем увеличился в n1 = 3,00 раза, затем водород был изохорно охлажден так, что его давление уменьшилось в n2 = 3,00 раза. Найдите приращение DS энтропии в ходе из указанных процессов.
Реальные газы
2.86. Определите, используя уравнение Ван-дер-Ваальса, давление р, которое будет производить кислород, содержащий количество вещества n = 1,0 моль, если он занимает объем V = 0,50 л при температуре T = 300 К. Сравните полученный результат с давлением, вычисленным по уравнению Клапейрона– Менделеева.
2.87.Атмосфера Венеры почти целиком состоит из углекислого газа
CO2. На поверхности планеты плотность газа r = 0,070 г/см3, его температура T = 750 К. Найдите давление p газа. Газ считать ван-дер-ваальсовским
скритическими параметрами pкр = 73 атм, Vкр = 94 см3/моль. Сравните результат с давлением pид идеального газа при тех же условиях.
2.88.В сосуде вместимостью V = 0,30 л находится углекислый газ, содержащий количество вещества n = 1,0 моль при температуре T = 300 К.
Определите давление p газа: 1) по уравнению Клапейрона– Менделеева; 2) по уравнению Ван-дер-Ваальса.
121
2.89.Во сколько раз концентрация nкр молекул азота в критическом состоянии больше концентрации n0 молекул при нормальных условиях?
2.90.Давление p кислорода равно 7 Мпа, его плотность ρ = 100 кг/м3. Найдите температуру T газа, если: 1) газ идеальный; 2) газ реальный.
2.91. Найдите внутреннюю энергию U углекислого |
газа массой |
m = 132 г при нормальном давлении р0 и температуре T = 300 |
К в двух слу- |
чаях, когда газ рассматривают: 1) как идеальный; 2) как реальный.
2.92.Определите давление р водяного пара массой m = 1,0 кг, взятого при температуре T = 380 К и объеме V: 1) 1000 л; 2) 10 л; 3) 2,0 л.
2.93.Кислород массой m = 8,00 г занимает объем V = 20,0 см3 при
температуре T = 300 К. Определите внутреннюю энергию U газа, если: 1) газ идеальный; 2) газ реальный.
2.94. Вычислите постоянные а и b в уравнении Ван-дер-Ваальса для азота, если известны критические температура Ткр = 126 К и давление
ркр = 3,39 МПа.
2.95.Определите приращение ∆U внутренней энергии неона, содержащего количество вещества n = 1,00 моль, при изотермическом расширении его объема от V1 = 1,00 л до V2 = 2,00 л.
2.96.Вычислите критические температуру Ткр и давление ркр: 1) кислорода; 2) воды.
2.97. Объем углекислого газа массой m = 0,100 кг увеличился от V1 = 1,00×103 л до V2 = 1,00×104 л. Найдите работу A внутренних сил взаимодействия молекул при этом расширении газа.
2.98. Критическая температура аргона равна Ткр = 151 К и критическое давление ркр = 4,86 МПа. Определите по этим данным критический молярный объем Vmкр аргона.
2.99. В сосуде вместимостью V1 = 1,00 л содержится азот массой m = 10,0 г. Определите приращение ∆T температуры азота, если он расширяется в пустоту до объема V2 = 10,0 л.
2.100. Определите плотность ρ водяных паров в критическом состоя-
нии.
122
