
КОНТРОЛЬНАЯ РАБОТА № 1
Физические основы механики.
Молекулярная физика и термодинамика
Задача 1.01
Самолёт летит на высоте 4 км со сверхзвуковой скоростью. Звук дошёл до наблюдателя через 10 сек после того, как над ним пролетел самолёт. Определить скорость самолёта. Скорость звука считать неизменной и равной 320 м/с
Решение:
Начертим схему для расчёта:

Из схемы найдём R и А, затем найдём угол между ними:



По отнашению к наблюдателю на земле:

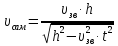

Ответ: Скорость самолёта составляет 533 км/час
Задача 1.21
К концам нити перекинутой через блок, подвешены грузы массами 50 и 100 г. Найти показание динамометра, на котором висит блок. Массой блока и трением пренебречь.
Решение:

Так как нить нерастяжима величина перемещения обоих грузов одинакова, азначит их ускорения равны.
а1 = а2 = а
Можно считать силу натяжения в нити везде одинаковой (пренебрегаем массой блока и нити, а также трением в блоке – по условию задачи).
Запишем уравнения второго закона Ньютона для каждого из грузов:



Вычитая второе аравнение системы из первого, получаем

Тогда

Для нахождения силы F упругости пружины динамометра рассмотрим силы действующие на блок. Условие равновесия блока имеет вид F + 2Т = 0
Откуда: F = 2Т = 0,67·2 = 1,3Н
Ответ:Динамометр покажет 1,3 Н.
Задача 1.41
Определить высоту круговой орбиты спутника относительно поверхности Земли, если он движется в экваториальной плоскости и с Земли кажется неподвижным.
Решение:
Из справочной литературы найдём необходимые данные:
 – масса
земли;
– масса
земли;
 –
радиус
земли;
–
радиус
земли;
 –
гравитационная
постоянная;
–
гравитационная
постоянная;
Т=86400 с-1 - период обращения, в нашем случае сутки.
Согласно закона всемирного тяготения:



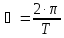



Ответ: Высота орбиты спутника составляет 36 тыс. км.
Задача 1.70
Самолёт массой 2 т движется в горизонтальном направлении со скоростью 50 м/с. Находясь на высоте 420 м, он переходит на снижение при выключенном двигателе и достигает посадочной полосы, имея скорость 30 м/с. Определить работу силы сопротивления воздуха во время планирующего полёта.
Решение:
Проведём расчёт энергии самолёта перед снижением и при достижении посадочной полосы. Разница и будет составлять работу силы сопротивления воздуха.
Кинетическая энергия самолёта при начале посадки:


Потенциальная энергия самолёта при начале посадки:


Кинетическая энергия самолёта при достижении посадочной полосы:
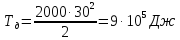
Работа силы сопротивления воздуха:


Ответ: Работа силы сопротивления воздуха составляет 1·107 Дж.
Задача 2.23
Средняя квадратичная скорость молекул некоторого газа при нормальных условиях равна 461м/с. Какое количество молекул содержится в 1г этого газа.
Решение:
Для решения задачи воспользуемся уравнением состояния идеального газа (уравнение Менделеева – Клапейрона):

где P - давление;
V – объём газа;
m – масса газа;
– молярная масса;
R – универсальная газовая постоянная, R=8,31Дж/(оС.моль);
Т – температура газа.
Подставим значение Р, использовав основное уравнение молекулярно-кинетической теории идеального газа:

где – плотность газа;
<кв> – среднее значение квадрата скорости молекул.
Выразим объем газа через плотность и массу:

Молярная масса вещества:

где
ν – количество вещества;
N – число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему);
Na – постоянная Авогадро, Na = 6,02·1023 моль-1.
Подставим полученные выражения в уравнение Менделеева-Клапейрона и выразим количество молекул:


При нормальных условиях принимают температуру 20оС.

Ответ: N=1,1.1022
Задача 2.43
При движении со скоростью 72 км/ч расходуется 20 % мощности двигателя. Определить в литрах расход бензина на 100 км пути. Мощность двигателя 100 л.с. КПД 30 %.
Решение:
При перемещении автомобиля на расстояние S его двигатель совершает работу

При
этом затрачивается масса топлива:


Найдём из справочной литературы недостающие данные и переведём все данные к одной системе СИ:
q = 46 Мдж/кг– удельная теплота сгорания бензина.
1 л.с. =0,746 кВт
1 вт/час = 3600 Дж
Произведём вычисления учитывая используется 20 процентов мощности:

Ответ: При заданных услолвиях на 100 км пути автомобиль тратит 5,4 кг бензина.
Задача 2.63
Определить термический КПД циклического процесса для одноатомного идеального газа. Цикл образован двумя изохорами и двумя изобарами. Известно, что при изобарном расширении объём увеличивается в 2 раза. А при изохорном охлаждении давление уменьшается в 2 раза.
Решение:
Для решения задачи используем первое начало термодинамики:
Q = ΔU + A,
где Q – количество теплоты, сообщенное системе окружающими системами;
ΔU – изменение внутренней системы;
А – работа расширения системы.
Изменение внутренней энергии системы:

где – количество вещества; R – универсальная газовая постоянная.
Работа расширения: А= Р(V2 – V1)
Где Р – давление газа

АВ – изохорный нагрев, V=const, Q=ΔU, ΔU<0 - газ получает тепло.
ВС – изобарное расширение, P=const, Q=ΔU+A, ΔU;A>0 – газ получает тепло.
СД – изохорное охлаждение, V=const, Q=ΔU, ΔU<0 - газ отдает тепло.
ДА – изобарное сжатие, P=const, Q=ΔU+A, ΔU;A<0 – газ отдает тепло.
Определим КПД цикла по формуле:

где ААВСД – работа газа за цикл,
QАВС – количество теплоты, полученное газом за цикл.
Работу газа за цикл найдем как площадь прямоугольника, ограниченного изобарами и изохорами:

Определим полученное газом количество теплоты:
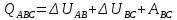

Выразим температуру из закона Бойля-Мариотта:

Тогда выражение примет вид:

Выполним аналогичные преобразования для ΔUBC и АВС:
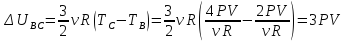

Тогда:

Рассчитаем КПД:

Ответ: η=15,4%
Задача 2.73
Тепловая машина, работающая по циклу Карно, имеет полезную мощность 2 кВт. Температура нагревателя 400 К, холодильника 300 К. Найти теплоту, отдаваемую холодильником за 10 мин работы.
Решение:
Термический КПД тепловой машины, работающей по циклу Карно (идеальная тепловая машина) (p–V-диаграмма на рисунке)


где T1 – температура нагревателя;
T2 – температура охладителя (холодильника).
С другой стороны, КПД цикла можно
определить по формуле:

где Q1 – количество теплоты, полученное рабочим телом (газом) от нагревателя;
Q1 – количество теплоты, переданное рабочим телом охладителю (холодильнику).
Полезная мощность тепловой машины определяется по формуле:

где t – время работы тепловой машины.
Тогда:

Таким образом, итоговая формула примет вид:

Ответ: Теплота отдаваемая холодильником Q2=900 кДж.
