Описание цикла Карно:

Цикл Карно в координатах P и V Цикл Карно в координатах T и S

Пусть тепловая машинасостоит из нагревателя с температуройT_H, холодильника с температуройT_Xирабочего тела.

Цикл Карно состоит из четырёх стадий:

1. Изотермическое расширение(на рисунке — процесс A→Б). В начале процесса рабочее тело имеет температуруT_H, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт емуколичество теплотыQ_H. При этом объём рабочего тела увеличивается.

2. Адиабатическое (изоэнтропическое) расширение(на рисунке — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.

3. Изотермическое сжатие(на рисунке — процесс В→Г). Рабочее тело, имеющее к тому времени температуруT_X, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплотыQ_X.

4. Адиабатическое (изоэнтропическое) сжатие(на рисунке — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия (поскольку при δQ= 0). Поэтому цикл Карно удобно представить в координатах T и S (температура и энтропия).

20.Энтропия: определение, закон возрастания энтропии

Энтропия— это сокращениедоступной энергиивещества в результате передачи энергии.Первый закон термодинамикигласит, что энергию невозможно создать или уничтожить. Следовательно, количество энергии во вселенной всегда такое же, как было и при ее создании.Второй закон термодинамикигласит, чтокоэффициентполезного действия ни одного реального (необратимого) процесса не может быть 100% при преобразовании энергии в работу.

Понятие энтропии впервые было введено Клаузиусомвтермодинамикев1865 годудля определения меры необратимогорассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она являетсяфункцией состоянияи остаётся постоянной приобратимых процессах, тогда как внеобратимых— её изменение всегда положительно.

,

где dS— приращение энтропии; δQ— минимальная теплота подведенная к системе; T — абсолютная температура процесса;

Применим неравенство Клаузиуса для описания необратимого кругового термодинамического процесса, изображенного на рис 3.13.

Рис. 3.13. Необратимый круговой термодинамический процесс

Пусть процессбудет необратимым, а процесс- обратимым. Тогда неравенство Клаузиуса для этого случая примет вид: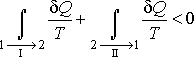

Так как процессявляется обратимым, для него можно воспользоваться соотношением(3.53), которое дает :

Подстановка этой формулы в неравенство(3.55)позволяет получить выражение :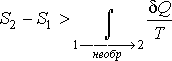

 Сравнение выражений позволяет записать следующее неравенство :,  в котором знак равенства имеет место в случае, если процессявляется обратимым, а знак больше, если процесс- необратимый.

Если рассмотреть адиабатически изолированную термодинамическую систему, для которой, то выражение примет видили в интегральной форме

Полученные неравенства выражают собойзакон возрастания энтропии, который можно сформулировать следующим образом:«В адиабатически изолированной термодинамической системе энтропия не может убывать: она или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс»

Записанное утверждение является ещё одной формулировкой второго начала термодинамики.

Таким образом, изолированная термодинамическая система стремится к максимальному значению энтропии, при котором наступает состояние термодинамического равновесия.