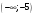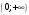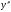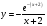Осень 13-весна 14 курс 1-2 ОрТОР (сейчас это называют ТОЛААД) / Матан / Вариант 14

Задание 1. Дана функция. Провести полное исследование функции и построить ее график.

1. .

1. Область определения функции – вся числовая ось, за исключением нулей знаменателя , т.е. .

2. .

Это функция общего вида.

3. Найдем производную первого порядка:

.

4. Найдем критические точки первого рода – точки, в которых первая производная равна нулю или не определена:

в числителе: 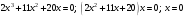, уравнение 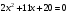корней не имеет, т.к. .

в знаменателе: .

Критические точки разбивают область определения на три интервала:

.

5. Найдем интервалы возрастания (где первая производная положительна) и убывания (где первая производная отрицательна) функции. Результат занесем в таблицу:

	+	+	-
	возрастает	возрастает	убывает

6. В точках функция не определена.

7. Найдем производную функции второго порядка:

8. Точное определение корня уравнения 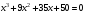аналитическим путем затруднено. Приблизительное значение корня 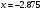. Производная второго порядка равна нулю в точке и не определена в точках . Это критические точки второго рода. Они разбивают область определения на интервалы: .

9. Найдем интервалы выпуклости функции. Результаты отобразим в таблице:

	+	-	+	+
	вогнута	выпукла	вогнута	вогнута

10. - точка перегиба функции, .

11. Находим наклонные асимптоты y=kx+b.

,

.

Кривая имеет горизонтальную асимптоту .

Кривая имеет вертикальные асимптоты .

12. Находим точки пересечения графика функции с осями координат.

С осью Ox: при у=0 , M1(-2,0), M2(3,0).

Ось Oy не пересекает.

13. Построим график функции:

2. 

1. Область определения функции – вся числовая ось, за исключением точки , в которой знаменатель обращается в ноль, т.е. .

2. .

Это функция общего вида.

3. Найдем производную первого порядка:

4. Найдем критические точки первого рода – точки, в которых первая производная равна нулю или не определена:

в числителе: ; в знаменателе: .

Критические точки разбивают область определения на три интервала:

.

5. Найдем интервалы возрастания (где первая производная положительна) и убывания (где первая производная отрицательна) функции. Результат занесем в таблицу:

	-	+	+
	убывает	возрастает	возрастает

6. Функция достигает минимума в точке .

Значения функции в точке экстремума: .

В точке значение функции не определено.

7. Найдем производную функции второго порядка:

8. Найдем критические точки второго рода – точки, в которых вторая производная равна нулю или не определена:

в числителе: уравнение корней не имеет, т.к. .

в знаменателе: .

Критическая точка разбивают область определения на два интервала:.

9. Найдем интервалы выпуклости функции. Результаты отобразим в таблице:

	+	-
	вогнута	выпукла

10. Находим наклонные асимптоты y=kx+b.

,

,

.

Кривая имеет горизонтальную асимптоту в положительной (правой) полуплоскости.

Кривая имеет вертикальную асимптоту .

11. Находим точки пересечения графика функции с осями координат.

Не пересекает ось Ox.

С осью Oy: при x=0 y=-0,068, M2(0,-0,068).

12. Построим график функции:

Задание 2. Найти наибольшее и наименьшее значения функции на замкнутом интервале .

1. Найдем точки экстремума функции в интервале . Для этого вычислим первую производную:

.

Найдем точки, в которых производная равна нулю или не существует:

.

Интервалу принадлежат все три точки.

Критические точки разбивают интервал на четыре:

.

Найдем интервалы возрастания (где первая производная положительна) и убывания (где первая производная отрицательна) функции. Результат занесем в таблицу:

	+	-	+	-
	возрастает	убывает	возрастает	убывает

Следовательно, точки - точки максимума функции на интервале.

Точка - точка минимума функции на интервале.

2. Значение функции в точке : .

Значение функции в точке : .

Значение функции в точке : .

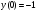3. Значение функции на концах интервала:

4. Наибольшее значение функции на замкнутом интервале : Наименьшее значение функции на замкнутом интервале : .