36.Построение произвольной прямой _|_ прямой общего положения.

Построить произвольную прямую d, _|_ заданной прямой n общего положения.

37.Комплексные задачи по нахождению искомого элемента.

Опр.-Комплеусными задачами, в которых на искосмый элемент наложены два условия и более.

Общая схема решения.

1)Вводятся вспомогательные геометрические фигуры(множества), каждая из которых в отдельности удовлетворяет одному из однозначных условий, наложенных на искомый элемент.

Однозначным называется условие, которому удовлетворяет только одна графически простая геометрическая фигура( прямая, окружность,плоскость, цилиндр, конус, сфера), образованная множеством искомых элементов.

2)Определяется искомый элемент как результат пересечения введенных в задачу вспомогательных множеств.

38.Алгоритм решения комплексных задач.

1)Анализ условий задачи- а) изучаются заданные геометрические фигуры и их пространственное расположение

Б) Устанавливается взаимосвязь искомого элемента с каждой из заданных геометрических фигур в виде однозначных условий, которым соответствуют графически простые вспомогательные множества.Колличество множеств = кол-ву условий.

3)Алгоритм решения- содержание и последовательность пространственных операций, необходимых для определения искомого элемента выявляется на основе проведенного анализа

4)Исследование- проводится с целью выявления условий существования решения и кол-ва возможных решений.

5)Построение К.Ч.-выполняется в установленной алгоритмом последовательности при наименьшем кол-ве построений.

39.Решение комплексной задачи по построению _|_ на прямую общего положения.

Из точки А опустить _|_ на прямую d общего положения.

Анализ.

Искомая прямая n должна:

1)проходить через точку А и быть _|_ прямой d-этому соответствует множество прямых, образующих (дельта) (f перес. n), проходящую через точку А и _|_ прямой d

2)проходить через точку А и пересекать прямую d-этому соответствует множество прямых, проходящих через точку А и пересекающих прямую d. Этим множеством является пл-ть Г,заданная прямой d и точкой А.

3) пересечение двух новых множеств

40.Способы преобразования комплексного чертежа:необходимость преобразования,типы преобразования.

Можно ли по чертежу сразу определить расстояние между двумя // прямыми а и b ?

1)изменением положения пл-ей проекций при неизменном положении Г.О.

2)изменением положения Г.О. относительно пл-ей проекций

3)изменением направления проецирования относительно пл-ей проекций

41.Способ замены пл-ей проекций:сущность, св-ва.

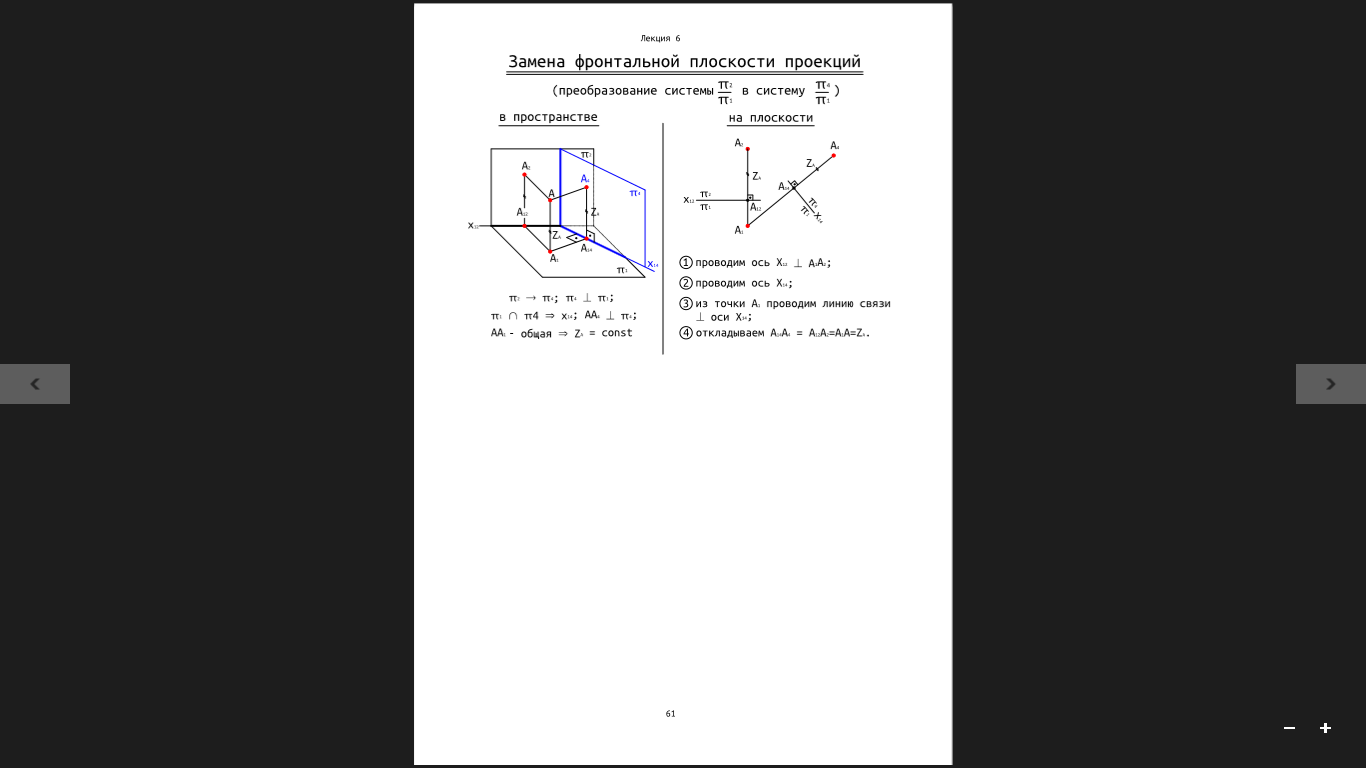
42.Преобразование чертежа методом замены фронтальной пл-и проекций.

43. Преобразование чертежа методом замены горизонтальной пл-и проекций.

44.Алгоритм способа замены пл-ей проекций.

1)На заданном чертеже проводим ось проекций Х12.

2)Проводим новую ось проекций в положении обусловленном задачей.

3)От незаменяемой проекции точки проводим линию связи _|_ новой оси проекций.

4)Замеряем расстояние от заменяемой проекции точки до оси проекций заменяемого поля и откладываем его на новом поле проекций вдоль новой линии связи от оси проекций нового поля.

45.Последовательные замены пл-ей проекций.

46.Преобразование прямой общего положения во фронталь методом замены пл-ей проекций.

Преобразовать прямую общего положения во фронталь.

Решение.

1)проводим ось проекций Х12 _|_ А1А2

2)проводим ось Х14//а1

3)из точек А1 и В1 проводим линии связи _|_ оси Х14

4)на линиях связи от оси Х14 откладываем ZА и Zв

А(а4)-фронталь, альфа-угол наклона а к п1

47.Преобразование прямой уровня во фронтально проецирующую методом замены пл-ти проекций.

Преобразовать прямую уровня во фронтально проецирующую.

Решение.

1)Проводим ось проекций Х12_|_ А1А2

2)проводим ось Х14 _|_h1

4)на линии связи от оси Х14 откладываем отрезок Z=ZA=Zв

h(h4)-фронтально проецирующая прямая.

48.Преобразование прямой общего положения в проецирующую прямую методом замены пл-ей проекций.

Преобразовать прямую общего положения в проецирующую.

Одно преобразование решения задачи не дает, т.к. новая пл-ть,_|_ прямой не будет _|_ ни одной из старых пл-ей проекций и, как следствие, не образует ни с одной прямой из них прямоугольной системы пл-ей проекций.

Порядок преобразования-Прямая общего полож.-Линия уровня-Проецирующая прямая

1)аналогично задаче 1

2)аналогично задаче 2