23.Алгоритм решения второй позиционной задачи.

Вид и положение вспомогательной плоскости (ВП)

Определяется

Видом и взаиморасполажением заданных поверхностей(Ф и )

ВП-могут быть

1)проецирующими плоскостями

2)сферическими, цилиндрическими или кононическими поверхностями.

Простотой и точностью построений

Проекции линии пересечения ВП с заданными поверхностями должны быть графически простыми линиями

1)отрезками прямой

2)дугой окружности

24.Решение задач по алгоритму второй позиционной задачи:опр. Линии пересечения двух плоскостей общего положения.

Построить линию пересечения MN пл-ей общего положения (сигма) (a перес. b) и (дельта) (с//d)

25.Решение второй позиционной задачи по алгоритму первой позиционной.

Построени линии пересечения пл-ей, заданных многоугольниками, можно упростить, если вспомогательные проецирующие пл-ти проводить не произвольно,а через какие-либо две из сторон многоугольников.

Построить линию пересечения MN двух пл-ей общего положения (дельта)АВС и (сигма)DEFK, заданных многоугольниками.

1)проекция А2В2 стороны АВ многоугольника АВС, через которую проведена вспомогательная пл-ть Г(Г_|_п2), уже является фронтальной проекцией линии пересечения пл. Г и многоугольника АВС

2)в дальнейшем требуется лишь найти вторую проекцию линии пересечения пл-и Г с многоугольником DEFK

3)точка M пересечения двух вышеупомянутых линий является искомой.

4)аналогично определяется вторая точка N линия пересечения MN (по пл-и Г’-АС)

Определение видимости-1-На п2 по фронтально конкурирующим точкам 2 и 7

2-На п1 по горизонтально конкурирующим точкам 5 и 6

26.Взаимная // прямой и пл-ти.

Теорема стереометрии-Если прямая // какой-либо прямой,принадлежащей пл-ти, то данные прямая и пл-ть //

Чкрез точку М провести прямую d, // пл-ти Г(АВС)

27.Взаимная // двух плоскостей.

Теорема стереометрии-Если две пересекающиеся прямые одной пл-ти соответственно // двум прямым другой пл-ти,то эти пл-ти- //

Через точку М провести пл-ть (сигма), // пл-ти Г(АВС)

28.Взаимная перпендик-ть:признаки взаимной перпендик-ти прямых и пл-ей

1)две прямые называются взаимно _|_, если угол между ними равен 90

2)если прямая _|_ каждой из двух пересекающихся прямых,принадлежащих пл-ти,то эта прямая и пл-ть взаимно _|_

3)прямая _|_ пл-ти,_|_ к любой прямой, принадлежащей этой пл-ти

4)если пл-ть проходит через _|_ к другой пл-ти,то она _|_ этой пл-ти

29.Проекции прямого угла: частные случаи проецирования прямого угла

Любой линейный угол проецируется на пл-ть проекций в истинную величину, если его стороны // этой пл-ти.

Теорема1-Если одна сторона прямого угла // пл-ти проекций,а другая является прямой общего положения, то прямой угол проецируется на эту пл-ть проекций без искажения, т.е. в прямой же угол.

30.Проекция прямого угла,одной из сторон которого является горизонталь.

31.Проекция прямого угла одной из сторон которого является фронталь

32.Прямая _|_ плоскости:признаки перпендикулярности на чертеже.

Теорема2-Если прмая_|_ к пл-ти в пространстве,то на комплексном чертеже горизонтальная проекция прямой _|_ горизонтальной проекции горизонтали, а фронтальная проекция- _|_ к фронтальной проекции фронтали этой пл-ти.

33.Проведение _|_ к плоскости из заданной точки пространства.

Провести _|_ из точки А к пл-ти (сигма)(а перес. b)

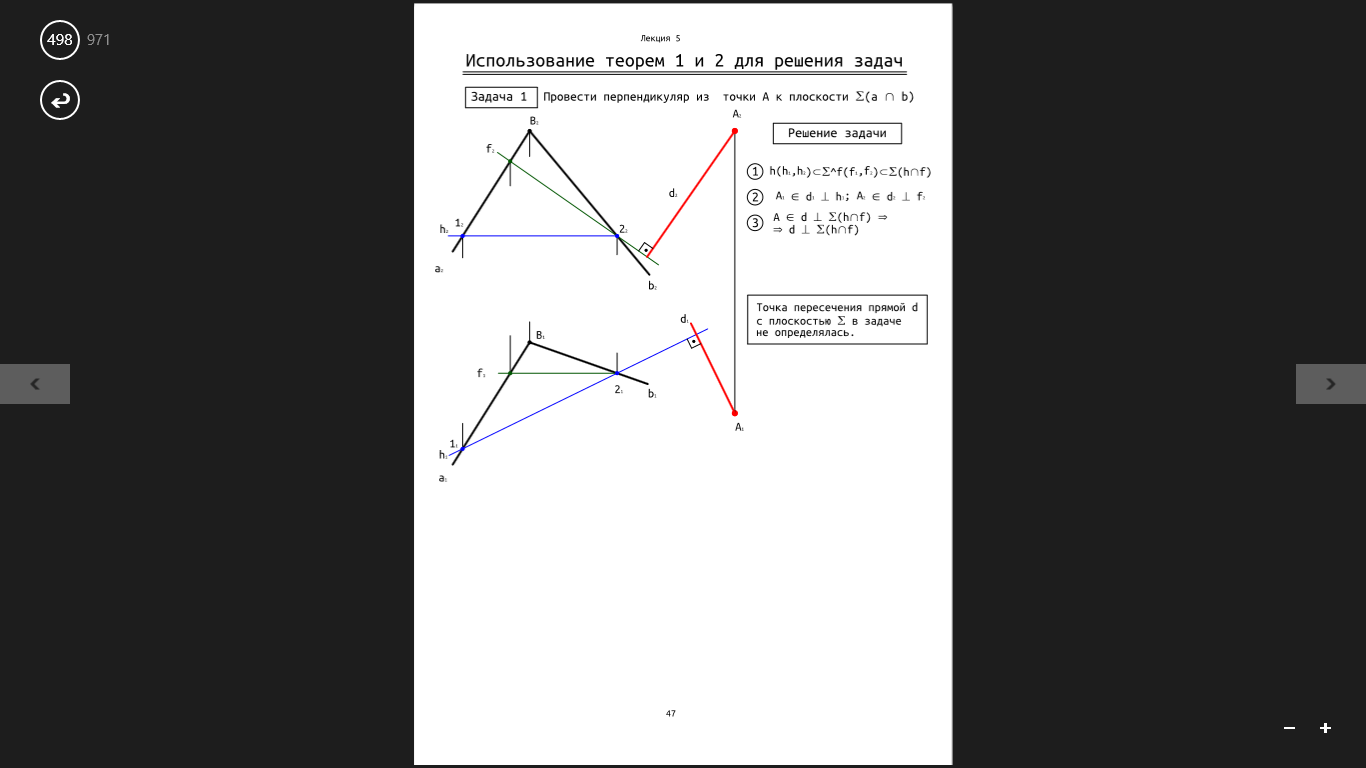
Точка пересечения прямой d с пл-тью (сигма) в задаче не определялась.

34.Построение пл-ти _|_ прямой общего положения.

Через точку А провести пл-ть (сигма) _|_ прямой общего положения.

Решение-Через точку А достаточно провести две прямые, каждая из которых была бы _|_ заданной прямой d.

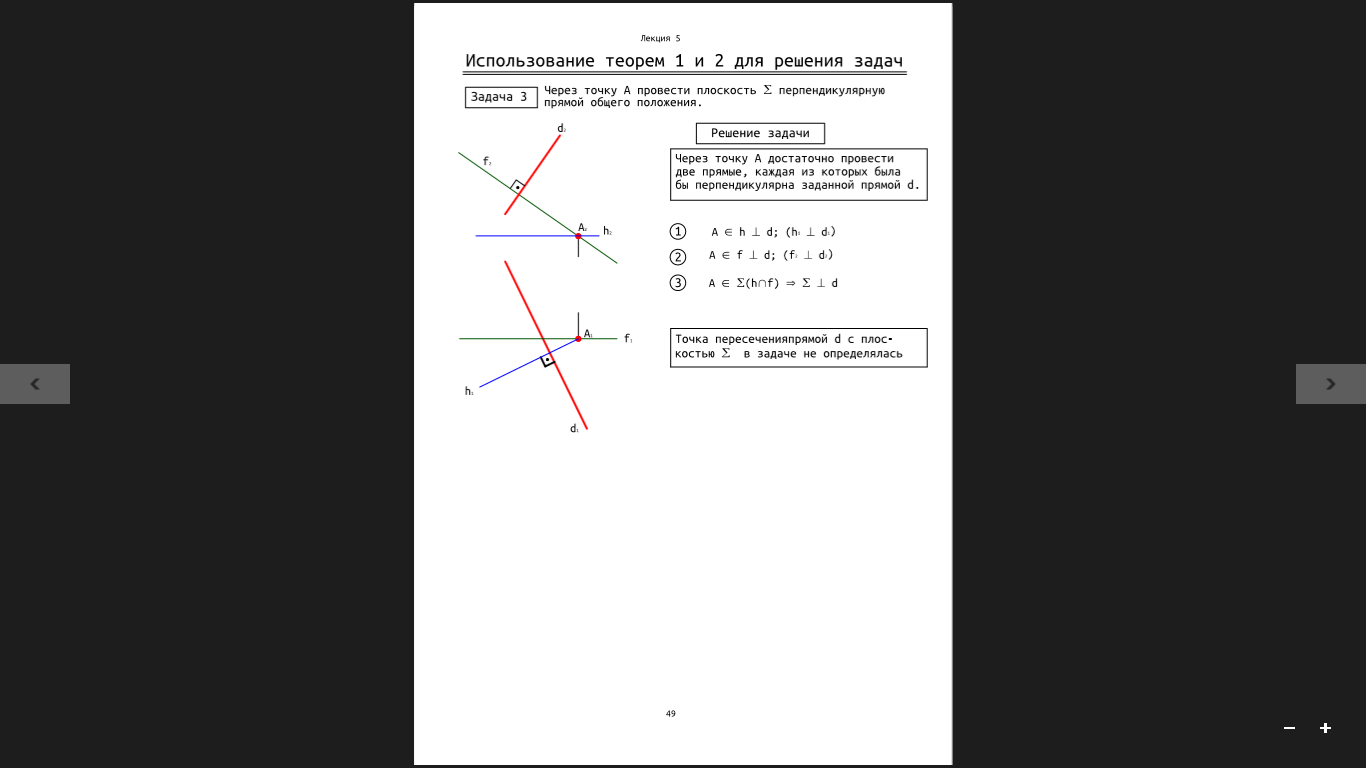
Точка пересечения d с пл-тью (сигма) в задаче не определялась

35.Взаимно _|_ прямые общего положения.

Если стороны прямого угла являются прямыми общего положения,то прямой угол на каждую из трех пл-ей проекций(п1…п3)проецируется с искажением.

При построении проекций такого угла необходимо исходить из следующих положений:

1)Если две прямые взаимно _|_, то через каждую из них можно провести пл-ть,_|_ к другой прямой.

2)Если прямая _|_ к пл-ти,то она _|_ любой прямой, принадлежащей этой пл-ти.

Вывод-Построение взаимно _|_ прямых общего положения сводится к построению пл-ти _|_ к заданной прямой общего положения.