
Осень 13-весна 14 курс 1-2 ОрТОР (сейчас это называют ТОЛААД) / Матан / vopr_12_1
.docВопрос 1,2.Теория множества. Операции над множествами.
Множеством называется совокупность определенных вполне различаемых объектов, рассматриваемых как единое целое. Создатель теории множеств Георг Кантор давал следующее определение множества — «множество есть многое, мыслимое нами как целое».
Отдельные объекты, из которых состоит множество, называются элементами множества.
Множества бывают конечные и бесконечные. Множества называются конечным, если число его элементов конечно, т.е. если существует натуральное число n, являющееся числом элементов множества. А={a1, a2,a 3, ..., an}. Множество называется бесконечным, если оно содержит бесконечное число элементов. B={b1,b2,b3, ...}. Например, множество букв русского алфавита — конечное множество. Множество натуральных чисел — бесконечное множество.
число элементов в конечном множестве M называется мощностью множества M и обозначается |M|.Пустоемножество — множество, не содержащее ни одного элемента — ∅. Два множества называются равными, если они состоят из одних и тех же элементов, т.е. представляют собой одно и тоже множество. Множества не равны X ≠ Y, если в Х есть элементы, не принадлежащие Y, или в Y есть элементы, не принадлежащие Х. Символ равенства множеств обладает свойствами:
-
Х=Х; — рефлексивность
-
если Х=Y, Y=X — симметричность
-
если X=Y,Y=Z, то X=Z — транзитивность.
Согласно такого определения равенства множеств мы естественно получаем, что все пустые множества равны между собой или что то же самое, что существует только одно пустое множество.
Говорят,
что множество А содержится
в множестве В ( рис.1 )
или множество А является подмножеством множества В ( в
этом случае пишут А ![]() В), если
каждый элемент множества А одновременно
является элементом множества В .
Эта зависимость между множествами
называется включением.
Для любого множества А имеют
место включения:
В), если
каждый элемент множества А одновременно
является элементом множества В .
Эта зависимость между множествами
называется включением.
Для любого множества А имеют
место включения: ![]()
![]() А
и А
А
и А ![]() А .
А .
-
Сумма ( объединение ) множеств А и В ( пишется А
 В )
есть множество элементов, каждый из
которых принадлежит либо А ,
либо В.
Таким образом, е
В )
есть множество элементов, каждый из
которых принадлежит либо А ,
либо В.
Таким образом, е  А
А  В тогда
и только тогда, когда либо е
В тогда
и только тогда, когда либо е 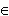 А , либо е
А , либо е  В .
В .
-
Произведение ( пересечение ) множеств А и В ( пишется А
 В ,
рис.2 ) есть множество элементов,
каждый из которых принадлежит и А ,
и В .
Таким образом, е
В ,
рис.2 ) есть множество элементов,
каждый из которых принадлежит и А ,
и В .
Таким образом, е 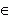 А
А  В тогда
и только тогда, когда е
В тогда
и только тогда, когда е  А и е
А и е  В .
В . -
Разность множеств А и В ( пишется А – В , рис.3 ) есть множество элементов, которые принадлежат множеству А , но не принадлежат множеству В.Это множество называется также дополнением множества В относительно множества А.
-
Симметричная разность множеств А и В ( пишется А \ В ) есть множество:
А \ В = ( А – В ) ![]() ( В – А ).
( В – А ).
Вопрос 3.Комплексные числа. Действия над КЧ в алг.форме.
Комплексные числа записываются в виде: a+ bi. Здесь a и b – действительные числа, а i – мнимая единица, т.e. i 2 = –1. Число a называетсяабсциссой, a b – ординатой комплексного числа a+ bi. Два комплексных числа a+ bi и a – bi называются сопряжёнными комплексными числами.
Сложение. Суммой комплексных чисел a+ bi и c+ di называется комплексное число ( a+ c ) + ( b+ d ) i. Таким образом, при сложениикомплексных чисел отдельно складываются их абсциссы и ординаты.
Это определение соответствует правилам действий с обычными многочленами.
Вычитание. Разностью двух комплексных чисел a+ bi (уменьшаемое) и c+ di (вычитаемое) называется комплексное число ( a – c ) + ( b – d ) i.
Таким образом, при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.
Умножение. Произведением комплексных чисел a+ bi и c+ di называется комплексное число:
( ac – bd ) + ( ad + bc ) i . Это определение вытекает из двух требований:
1) числа a+ bi и c+ di должны перемножаться, как алгебраические двучлены,
2) число i обладает основным свойством: i 2 = –1.
Деление. Разделить комплексное число a+ bi (делимое) на другое c+ di (делитель) - значит найти третье число e+ f i (чатное), которое будучи умноженным на делитель c+ di, даёт в результате делимое a+ bi.
Если делитель не равен нулю, деление всегда возможно.
П р и м е р . Найти ( 8 + i ) : ( 2 – 3i ) .
Р
е ш е н и е . Перепишем это отношение в
виде дроби: ![]()
Умножив её числитель и знаменатель на 2 + 3i
и выполнив все преобразования, получим:

Вопрос 4.Тригонометрическая форма комплексного числа.Модуль и аргумент комплексного числа.
Тригонометрическая
форма комплексного числа. Абсциссу a и
ординату b комплексного
числа a + bi можно
выразить через его модуль r и
аргумент ![]() :
:

Операции с комплексными числами, представленными в тригонометрической форме.

Это знаменитая формула Муавра.
![]()
Здесь k - целое. Чтобы получить n различных значений корня n-ой степени из z необходимо задать n последовательных значений для k ( например, k = 0, 1, 2,…, n – 1 ) .
Вопрос 20. Аналитическое определение модуля и направляющих косинусов вектора через проекции.
-
Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.
Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам.
Если
в пространстве задан вектор ![]() ,
то его направляющие косинусы вычисляются
по формулам:
,
то его направляющие косинусы вычисляются
по формулам:
![]()
Здесь ![]() ,
, ![]() и
и ![]() -
углы, которые составляет вектор с
положительными направлениями осей
-
углы, которые составляет вектор с
положительными направлениями осей ![]() ,
, ![]() и
и ![]() соответственно.
соответственно.
-
Длиной (модулем) вектора
 называется неотрицательное
число,
равное расстоянию между его началом и
концом, то есть длина вектора - это длина
отрезка
называется неотрицательное
число,
равное расстоянию между его началом и
концом, то есть длина вектора - это длина
отрезка  .
Длина
.
Длина  обозначается
обозначается 
![]()
-
Длина вектора, заданного координатами, равна корню квадратному из суммы квадратов его координат.
Вопрос 46.Характеристическое ур-е м-цы линейного преобразования.
Характеристическим многочленом преобразования или матрицы А называется многочлен -й степени относительно , имеющий вид , где - единичная матрица порядка .
Характеристическим уравнением линейного преобразования f или матрицы А называется уравнение
,где - матрица этого преобразования в некотором базисе, а его корни называются собственными числами линейного преобразования, а также матрицы .
Вопрос 47.Квадратичные формы.Приведение квадратичной формы к каноническому виду.
Квадратичной формой от переменных называется симметрический однородный многочлен второй степени от этих переменных
, (3)
где .
Если ввести матрицу из коэффициентов квадратичной формы (3)
и матрицу-столбец из переменных
,
то, пользуясь правилом умножения матриц, квадратичную форму (3) можно записать в матричном виде
.
Привести квадратичную форму (9.8) к каноническому виду - значит представить ее следующим образом:
. (4)
Матрица В, соответствующая квадратичной форме (4), диагональна.
Так как матрица симметрическая вещественная, задача приведения к каноническому виду квадратичной формы (3) сводится к задаче приведения к диагональному виду матрицы симметрического линейного преобразования с помощью ортогональной матрицы (ортогонального преобразования).
Корни характеристического уравнения матрицы называют характеристическими числами квадратичной формы (3), а направления собственных векторов, соответствующих характеристическим числам, главными направлениями квадратичной формы.
Правило нахождения ортогонального преобразования, приводящего квадратичную форму переменных к каноническому виду:
1) записать квадратичную форму в симметрическом виде;
2) записать матрицу квадратичной формы;
3) составить характеристическое уравнение ;
4) найти собственные значения ;
5) записать однородную систему уравнений исли ввести матрицу из коэффициентов квадратичной формы (3)
и матрицу-столбец из переменных
,
то, пользуясь правилом умножения матриц, квадратичную форму (3) можно записать в матричном виде
.
Привести квадратичную форму (9.8) к каноническому виду - значит представить ее следующим образом:
. (4)
Матрица В, соответствующая квадратичной форме (4), диагональна.
Так как матрица симметрическая вещественная, задача приведения к каноническому виду квадратичной формы (3) сводится к задаче приведения к диагональному виду матрицы симметрического линейного преобразования с помощью ортогональной матрицы (ортогонального преобразования).
Корни характеристического уравнения матрицы называют характеристическими числами квадратичной формы (3), а направления собственных векторов, соответствующих характеристическим числам, главными направлениями квадратичной формы.
Правило нахождения ортогонального преобразования, приводящего квадратичную форму переменных к каноническому виду:
1) записать квадратичную форму в симметрическом виде;
2) записать матрицу квадратичной формы;
3) составить характеристическое уравнение ;
4) найти собственные значения ;
5) записать однородную систему уравнений и найти собственные векторы матрицы ;
6) образовать новый ортогональный базис из собственных векторов и составить ортогональную матрицу перехода ;
7) записать канонический вид квадратичной формы.
найти собственные векторы матрицы ;
6) образовать новый ортогональный базис из собственных векторов и составить ортогональную матрицу перехода ;
7) записать канонический вид квадратичной формы.
Вопрос 48.Пов второго порядка.
Общее уравнение поверхности второго порядка Ax2 + By2 + Cz2 + 2Fyz + 2Gzx + 2Hxy + 2Px + 2Qy + 2Rz + D = 0, где x, y, z − координаты точек поверхности, A, B, C, ... − действительные числа
