МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Расчетно-графическая работа №4

Расчет и анализ переходных процессов в линейных цепях

Вариант №139

Выполнил: студент группы 4Т61 21 марта 2018 г. Д. Р. Кошкин

(подпись)

Проверил преподаватель: к. т. н., доцент « »______2018г. О. В. Васильева

(подпись)

Томск 2018

Расчет переходных процессов в линейных электрических цепях

I. Для заданной схемы при коммутации ключа K₁ в момент времени t = 0, когда ключ K₂ еще не сработал, выполнить следующее:

1. При постоянном источнике ЭДС e(t) = E или тока J(t) = J опреде­лить ток i(t) или напряжение u_J(t):

а) классическим методом;

б) операторным методом;

построить график зависимости тока i(t) или напряжения u_J(t).

2. При гармоническом источнике ЭДС или тока определить ток i(t) или напряжение u_J(t):

а) классическим методом;

б) комбинированным (операторно-классическим) методом;

на интервале времени построить график зависимости тока i(t) или напряжения u_J(t).

3. При импульсном источнике ЭДС 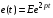или тока 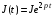и нулевых начальных условиях определить интегралом Дюамеля ток i(t) или напряжение u_J(t), построить их график зависимости (p – корень характеристического уравнения из п. 1, а).

II. Для заданной схемы с постоянным источником ЭДС e(t) = E или тока J(t) = J при коммутации ключа K₂ в момент времени t=0, когда ключ K₁ давно уже сработал, определить ток i(t) или напряжение u_J(t):

а) классическим методом;

б) операторным методом;

в) методом переменных состояния;

построить график зависимости тока i(t) или напряжения u_J(t).

III. Проанализировать методы расчета, результаты вычислений, графики зависимостей и сформулировать выводы по работе.

Исходные данные

Для заданной схемы дано:

Таблица 1

E	α	ω	R	L	C
В	град	1/c	Ом	Гн	мкФ
300	90	200	80	0,08	125

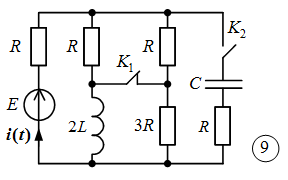
Рисунок 1 – Исходная схема

Задание I

В первом задании ключ К₂ еще не сработал, происходит коммутация ключа К₁.

1. Постоянные источники

Рисунок 2 – Схема до коммутации до размыкания ключа К₂

а) Классический метод расчета

На схеме цепь первого порядка, так как присутствует только один реактивный элемент (конденсатор).

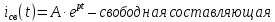
A – постоянная интегрирования

p – корень характеристического уравнения

1. Независимые начальные условия

В данной схеме независимым начальным условием является ток катушки индуктивности 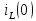, так как он не меняется скачком при переключении ключа (по 1 закону коммутации). Используется схема до коммутации, индуктивность заменяется на закоротку.

Рисунок 3 – Схема для расчета ННУ

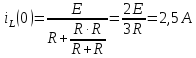(по закону Ома)

2. Зависимые начальные условия

Для данной схемы зависимыми начальными условиями является искомый ток i(0+). Заменяя индуктивность на источник тока по направлению 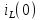. Схема используется после коммутации.

Рисунок 4 – Схема для расчета ЗНУ

С помощью метода контурных токов нашел i(0+):

Решив данную систему уравнений получил: 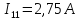. Тогда

3. Принужденная составляющая

Далее нашел принужденную составляющую искомого тока, используя схему после коммутации и индуктивность заменяя на закоротку.

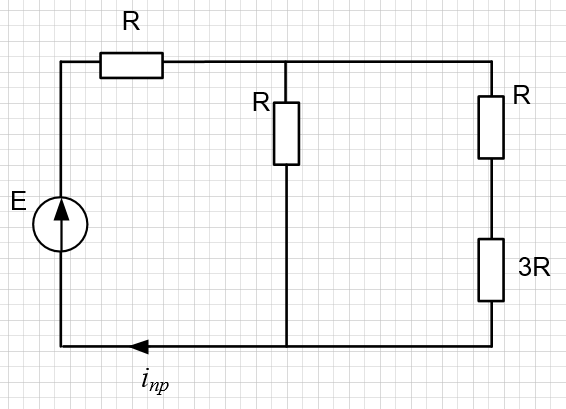Рисунок 5 – Схема для нахождения принужденной составляющей

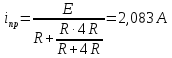
4. Корень характеристического уравнения

При составлении схемы для нахождения корня ХУ, индуктивность остаются, обозначаясь 2Lp. Источник ЭДС заменяется на закоротку. Схема после коммутации.

Рисунок 6 – Схема для нахождения корня ХУ

Нашел и приравнял к нулю. Получил c^-1

5. Нахождение постоянной интегрирования

A

6. Окончательный ответ

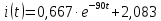A

7. Привожу Решение в MathCAD

Рисунок 7 – Решение в MathCAD

8. Построил график

Рисунок 8 – Построение графика в MathCAD

б) Операторный метод расчета

1. Независимые начальные условия

ННУ определяется классическим методом, аналогично предыдущему пункту

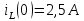
2. Операторная схема замещения после коммутации

ЭДС обозначается как E/p. Индуктивность L меняется на индуктивность Lp с последовательно подключенным ЭДС i_L(0)*L, направленным по течению тока. Источники ЭДС активные. Искомый ток обозначается I(p). В результате получится следующая схема

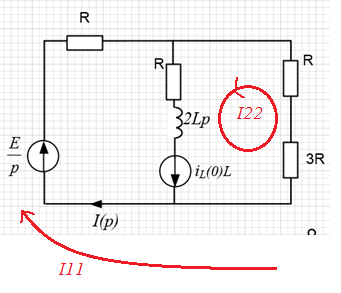Рисунок 9 – Операторная схема замещения после коммутации

3. Используя операторную схему замещения после коммутации, нахожу изображение I(p) тока i(t) по контурным токам:

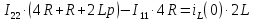
Тогда

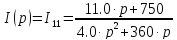
4. Нахожу оригнал через MathCAD. Таким образом:

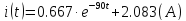
Ток , рассчитанный по классическому методу совпал со значением, полученным операторным методом, что говорит о верности вычисления.

5. Привожу Решение в MathCAD

Рисунок 10 – Решение в MathCAD

6. Построил график i(t):

– постоянная времени.

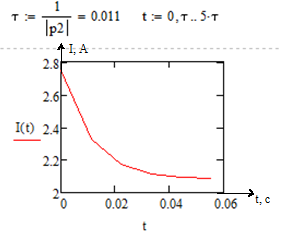Рисунок 11 – График i(t) переходного процесса

2. Гармонические источники

Определяю ток классическим методом. Принимаю ЭДС равным:

.

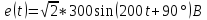Определил значение ЭДС через комплексные составляющие:

.

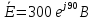Сопротивление катушки:

.

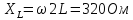Рисунок 10 – Схема до коммутации с гармоническим источником

а) Классический метод расчета

1. Независимые начальные условия

Здесь необходимо найти так же ток индуктивности в момент времени перед коммутацией, все происходит по тому же алгоритму, что и с постоянным источником, но индуктивность уже не меняется на разрыв, так как имеет реактивное сопротивление.

Рисунок 11 – Схема для нахождения ННУ

Определяю ННУ, т.е. :

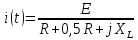(по закону Ома)

(по правилу разброса)

Или в другой записи:

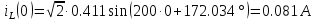
2. Зависимые начальные условия (по закону Ома)

Здесь необходимо найти ток на ЭДС 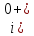сразу после коммутации ключа. Индуктивность будет меняться на пассивный источник тока с величиной по направлению .

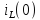Рисунок 12 – Схема для нахождения ЗНУ

С помощью контурных токов нашел.

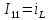
Решив эту систему, получил:

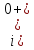
3. Принужденная составляющая

Определяю принужденную составляющую тока 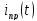по обобщенному закону Ома для цепи после коммутации:

Рисунок 13 – Схема для нахождения принужденной составляющей

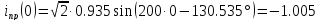
4. Корень характеристического уравнения

Корень выполняется аналогично предыдущему пункту.

Получил c^-1

5. Постоянная интегрирования

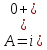
6. Окончательный ответ

7. Привожу Решение в MathCAD

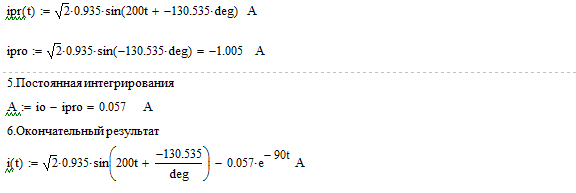Рисунок 14 – Решение в MathCAD

8. Построил графики

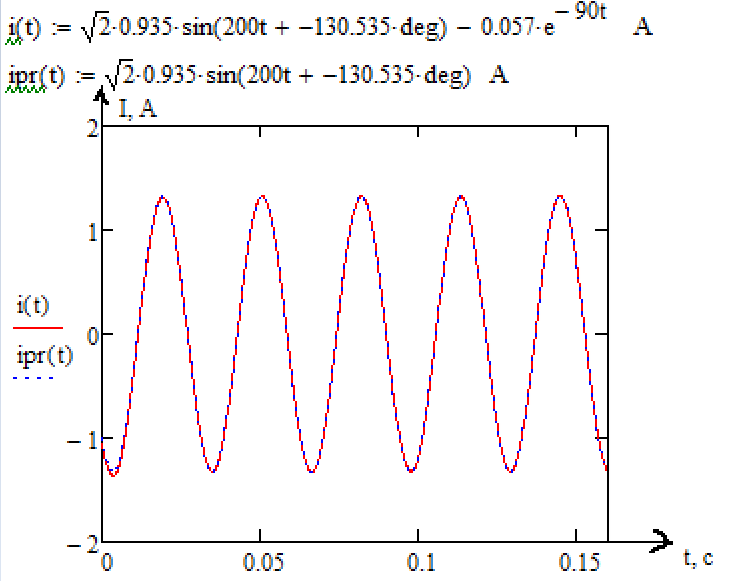Рисунок 15 – Построение графика в MathCAD

б) Комбинированный метод расчета

1. Независимые начальные условия

ННУ находятся классическим методом, поэтому значения можно взять из предыдущих расчетов.

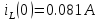
2. Принужденные составляющие

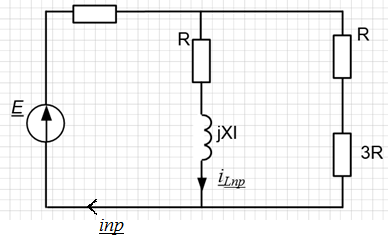Рисунок 16 – Схема для расчета принужденных составляющих

Принужденная составляющая для искомого тока аналогична классическому методу:

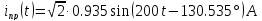
Определил принужденную составляющую тока индуктивности по правилу разброса:

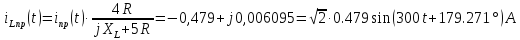
3. Свободные составляющие

Определил значения свободных составляющих для тока индуктивности при t=0

4. Операторная схема

Рассчитал операторную схему после коммутации для свободных составляющих, где источник ЭДС закорочен, а катушка заменена на катушку с источником ЭДС по направлению тока. Нашел изображение 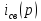тока 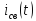по правилу разброса.

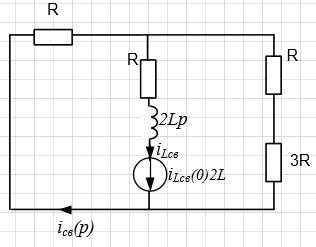Рисунок 17 – Операторная схема замещения после коммутации

5. Оригинал свободной составляющей

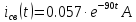
Таким образом

Ток 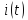, рассчитанный по классическому методу совпал со значением, полученным операторным методом, что говорит о верности вычисления.

6. Привожу Решение в MathCAD

Рисунок 18 – Решение в MathCAD

7. Далее построим график .

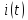Рисунок 19 – График i(t) переходного процесс

3. Испульсный источник

При импульсном источнике ЭДС и нулевых начальных условиях определил интегралом Дюамеля ток i(t) и построил график зависимости этого тока:

Рисунок 21 – Схема с импульсным источником

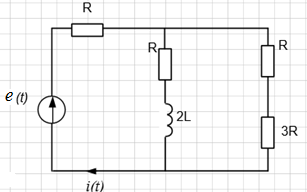
Искомый ток находится по формуле

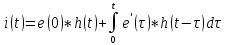
1. Независимые начальные условия

Принимаю, что ННУ равны нулю (ток), при дальнейших расчетах также принимаем e(t)=1

2. Зависимые начальные условия

Нахожу h(0+) после коммутации, индуктивность будет меняться на пассивный источник тока с величиной по направлению .

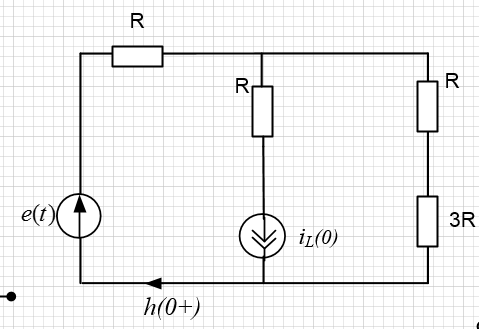Рисунок 22 – Схема для нахождения ЗНУ

Так как значение тока в ветви источника тока равно нулю, то

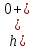
3. Принужденная составляющая

Находим h_пр, схема после коммутации, индуктивность меняется на закоротку.

Рисунок 23 – Схема для нахождения принужденной составляющей

По закону Ома:

4. Корень характеристического уравнения

При составлении схемы для нахождения корня ХУ, индуктивность остаются, обозначаясь 2Lp. Источник ЭДС заменяется на закоротку. Схема после коммутации.

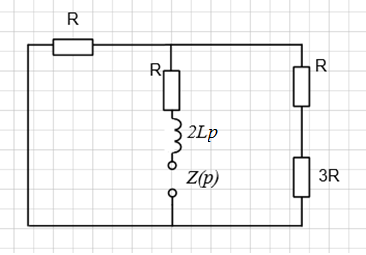Рисунок 24 – Схема для нахождения корня ХУ

Нашел и приравнял к нулю. Получил 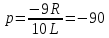c^-1

5. Постоянная интегрирования

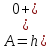6. См

7. Записал формулу:

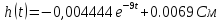
8. Решил формулу с интегралом Дюамеля:

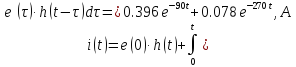
9. Расчет в маткад

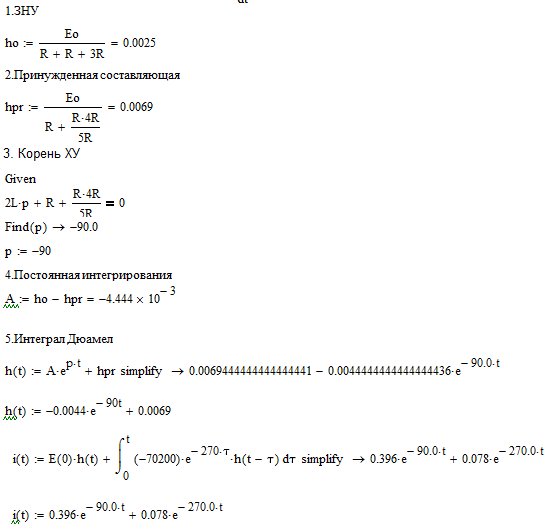Рисунок 25 – Расчеты MathCAD

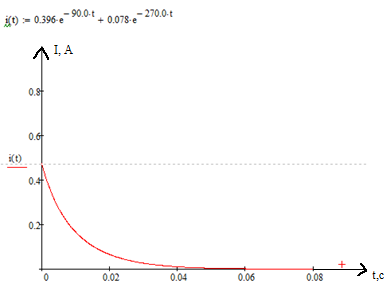Рисунок 26 – График переходного процесса при импульсном источнике тока.