
Лабораторные работы. Электричество и магнетизм / Физика. Эл. ЛР. Изучение электростатического поля
.docxЦель работы: экспериментально найти эквипотенциальные поверхности и силовые линии электростатического поля.
Приборы и принадлежности: нуль-гальванометр, щупы (подвижный и неподвижный), ванна со слабым раствором медного купороса, источник постоянного тока, набор электродов различной формы, цветные карандаши.
ХОД РАБОТЫ:
-
Закрепим неподвижный щуп на краю ванны с подключенным прямоугольным электродом.
-
Держа в руке щуп, будем передвигать его в ванне до тех пор, пока показания вольтметра в различных точках не будут одинаковыми и будем отмечать эти точки на листе.
-
Отметим на листе 7 эквипотенциальных кривых.
A – 1,3 В;
E – 3,9 В;
B – 1,9 В;
F – 4,7 В;
C – 2,6 В;
G – 5,4 В;
D – 3,2 В;
H – 6,1 В.
-
Перестроим конфигурацию электродов и проделаем тоже самое для круглого электрода.
A – 6,1 В;
E – 3,2 В;
B – 5,4 В;
F – 2,6 В;
C – 4,7 В;
G – 1,9 В;
D – 3,9 В;
H – 1,3 В.
-
Построим на основе эквипотенциальных кривых силовые линии поля.
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Что называется силовой линией? Как найти силовые линии в методе электролитической ванны?
Силовые линии электрического поля – это такие линии, в каждой точке которых касательная совпадает с вектором напряженности поля
В методе электролитической ванны изучение электростатического поля заменено изучением электрического поля, существующего в проводящей среде при протекании в ней постоянного тока. Такая замена оказывается правомочной, если потенциалы проводников, создающих поле, поддерживаются постоянными. В этом случае поверхности проводников можно считать поверхностями равного потенциала.
-
Что называется эквипотенциальной поверхностью? Докажите, что силовые линии идут всегда перпендикулярно эквипотенциальным поверхностям.
Эквипотенциальная поверхность – это поверхность, на которой скалярный потенциал данного потенциального поля принимает постоянное значение. Другое, эквивалентное, определение – поверхность, в любой своей точке ортогональная силовым линиям поля.
Поверхности в точке пересечения с нею. Действительно, пусть точки 1 и 2 находятся на одной и той же эквипотенциальной поверхности неподалеку друг от друга. Перенесем электрический заряд q вдоль эквипотенциальной поверхности из т.1 в т.2. Т.к. потенциалы в обеих точках одинаковы, то работа, совершаемая полем над зарядом равна нулю. Следовательно, сила, действующая на заряд F=qE, направлена перпендикулярно перемещению этого заряда. Т.к. заряд перемещался вдоль поверхности, то вектор Е перпендикулярен поверхности.
-
Как выглядят эквипотенциальные поверхности:
• точечного заряда,
• однородного поля?
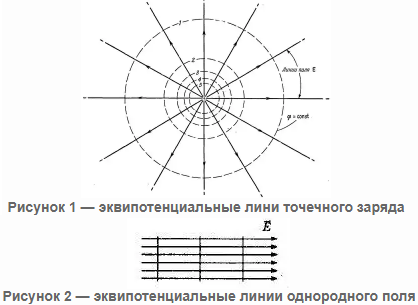
-
Как по картине силовых линий определить области высокой и низкой напряженности поля?
-
Как по картине эквипотенциальных поверхностей определить области высокой и низкой напряженности поля?
Густота эквипотенциальных поверхностей пропорциональна величине напряженности электрического поля в данной области. Действительно, пусть имеем пару эквипотенциальных поверхностей, потенциалы которых равны, соответственно, φ1 и φ2. Пусть расстояние между поверхностями в какой-либо области равно S2, а в некоторой другой – S2. Тогда величину напряженности поля в первой области можно оценить как Δφ/S1, а во второй как Δφ/S2. Здесь мы символом Δφ обозначили разность потенциалов Δφ2-Δφ1 между этими поверхностями. Ясно, что чем меньше расстояние между поверхностями, тем выше напряженность поля в данной области.
-
Могут ли силовые линии пересекаться одна с другой?
Силовые линии не могут касаться друг друга в точке, где нет зарядов.
Действительно, пусть две линии касаются друг друга в какой-либо точке. Тогда в точке касания двух линий густота этих линий будет бесконечной, т.е. напряженность поля в этой точке также будет бесконечной. Это невозможно, если только в этой точке нет заряда.
-
Могут ли эквипотенциальные поверхности пересекаться между собой?
Эквипотенциальные поверхности не могут пересекаться друг с другом в точке, где напряженность поля не равна нулю. Действительно, пересечение поверхностей означало бы, что в точках пересечения вектор напряженности поля имеет одновременно два различных направления, перпендикулярно как первой, так и второй поверхности. Это, очевидно, невозможно, если только в этих точках напряженность поля не равна нулю.
