
30.6. Алгоритм Флойда-Уоршола
Розглянемо задачу пошуку в графі найкоротшого шляху між кожною парою вершин. Звичайно, цю загальнішу задачу можна розв’язати багатократним застосуванням алгоритмів Дейкстри або Белмана-Форда з послідовним вибором кожної вершини графу як початкової. Проте є прямий спосіб розв’язання цієї задачі за допомогою алгоритму Флойда-Уоршола. У ньому довжини дуг можуть бути від’ємними, проте не може бути циклів із від’ємною довжиною.
Нехай G = (V, E)
– орієнтований граф. Внутрішніми
вершинами шляху a, x1, x2, …, xm–1, b
в графі G
є вершини x1,
x2,…,
xm–1.
Пронумеруємо вершини графу цілими
числами від 1 до n.
Позначимо як
![]() довжину найкоротшого шляху з вершиниі у
вершину j,
у якому як внутрішні можуть бути лише
перші k
вершин графу G.
Якщо між вершинами і
та j не
існує жодного шляху, то вважатимемо, що
довжину найкоротшого шляху з вершиниі у
вершину j,
у якому як внутрішні можуть бути лише
перші k
вершин графу G.
Якщо між вершинами і
та j не
існує жодного шляху, то вважатимемо, що
![]() =.
Зі сказаного випливає, що
=.
Зі сказаного випливає, що
![]() – це вага дуги (i, j),
а якщо такої дуги немає, то
– це вага дуги (i, j),
а якщо такої дуги немає, то
![]() =.
Для довільної вершини і
вважатимемо
=.
Для довільної вершини і
вважатимемо
![]() = 0.
Отже,
= 0.
Отже,![]() дорівнює довжині найкоротшого шляху з
вершиниі
у вершину j.
Позначимо як
дорівнює довжині найкоротшого шляху з
вершиниі
у вершину j.
Позначимо як
![]() матрицю розмірностіn n,
(і, j)-й
елемент якої дорівнює
матрицю розмірностіn n,
(і, j)-й
елемент якої дорівнює
![]() .
Якщо в заданому орієнтованому графіG
відома вага кожної дуги, то, виходячи з
попередніх міркувань, можна сформувати
матрицю
.
Якщо в заданому орієнтованому графіG
відома вага кожної дуги, то, виходячи з
попередніх міркувань, можна сформувати
матрицю
![]() ,
елементи якої дорівнюють довжинам
найкоротших шляхів між усіма парами
вершин графуG.
,
елементи якої дорівнюють довжинам
найкоротших шляхів між усіма парами
вершин графуG.
В алгоритмі Флойда-Уоршола
як початкову беруть матрицю
![]() .
Спочатку за нею обчислюють матрицю
.
Спочатку за нею обчислюють матрицю![]() ,
потім –
,
потім –![]() і процес повторюють доти, доки за матрицею
і процес повторюють доти, доки за матрицею![]() не буде обчислено матрицю
не буде обчислено матрицю![]() .
Розглянемо ідею, на якій ґрунтується
алгоритм Флойда-Уоршола. Припустимо,
що відомі:
.
Розглянемо ідею, на якій ґрунтується
алгоритм Флойда-Уоршола. Припустимо,
що відомі:
Найкоротший шлях із вершини і у вершину k, у якому як внутрішні використано лише перші (k – 1) вершин.
Найкоротший шлях із вершини k у вершину j, у якому як внутрішні використано лише перші (k – 1) вершин.
Найкоротший шлях із вершини і у вершину j, у якому як внутрішні використано лише перші (k – 1) вершин.
Оскільки за припущенням граф G не містить циклів із від’ємною довжиною, то один із двох шляхів – шлях із п. 3 чи об’єднання шляхів із пп. 1 і 2 – найкоротший шлях із вершини і у вершину j, у якому як внутрішні використано лише перші k вершин. Отже
|
|
30.2 |
Зі співвідношення (30.1) видно,
що для обчислення елементів матриці
![]() потрібні тільки елементи матриці
потрібні тільки елементи матриці![]() .
Тепер ми можемо формально описати
алгоритм Флойда-Уоршола для знаходження
в графі найкоротших шляхів між усіма
парами вершин.
.
Тепер ми можемо формально описати
алгоритм Флойда-Уоршола для знаходження
в графі найкоротших шляхів між усіма
парами вершин.
Алгоритм Флойда-Уоршола
Присвоювання початкових значень. Пронумерувати вершини графа G цілими числами від 1 до n. Побудувати матрицю
 ,
задавши кожний її (і, j)-й
елемент таким, що дорівнює вазі дуги,
котра з’єднує вершину і
з вершиною j.
Якщо в графі G
ці вершини не з’єднано дугою, то виконати
,
задавши кожний її (і, j)-й
елемент таким, що дорівнює вазі дуги,
котра з’єднує вершину і
з вершиною j.
Якщо в графі G
ці вершини не з’єднано дугою, то виконати
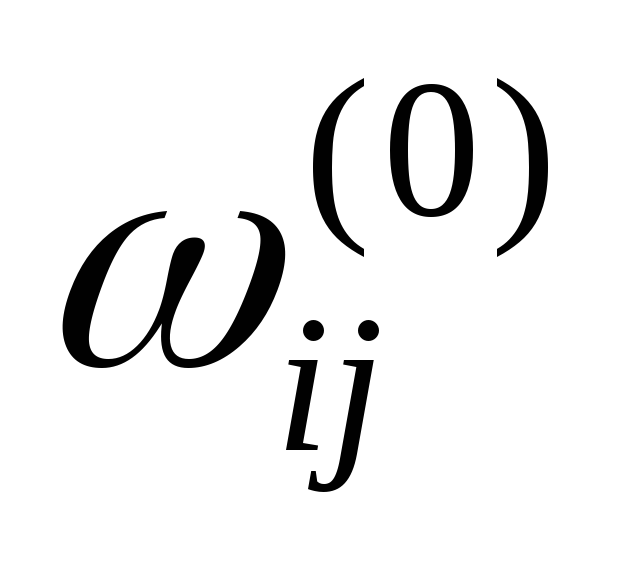 =.
Крім того, для всіх і
виконати
=.
Крім того, для всіх і
виконати
 = 0.
= 0.Цикл по всіх k, що послідовно набуває значення 1, 2, …, n, визначити за елементами матриці
 елементи матриці
елементи матриці ,
використовуючи рекурентне співвідношення
(30.1).
,
використовуючи рекурентне співвідношення
(30.1).
Після закінчення цієї процедури
(і, j)-й
елемент матриці
![]() дорівнює довжині найкоротшого шляху з
вершиниі
у вершину j.
дорівнює довжині найкоротшого шляху з
вершиниі
у вершину j.
Якщо під час роботи алгоритму
для якихось k
та і
виявиться, що
![]() < 0,
то в графіG
існує цикл із від’ємною довжиною, який
містить вершину і.
Тоді роботу алгоритму потрібно припинити.
< 0,
то в графіG
існує цикл із від’ємною довжиною, який
містить вершину і.
Тоді роботу алгоритму потрібно припинити.
Якщо заздалегідь відомо, що
в графі G
немає циклів із від’ємною довжиною, то
обсяг обчислень можна дещо зменшити. У
цьому разі для всіх і
та всіх k
має бути
![]() = 0.
Тому не потрібно обчислювати діагональні
елементи матриць
= 0.
Тому не потрібно обчислювати діагональні
елементи матриць![]() ,
,![]() , …,
, …,![]() .
Окрім того, для всіхі = 1, 2, …, n
справджуються співвідношення
.
Окрім того, для всіхі = 1, 2, …, n
справджуються співвідношення
![]() ,
,![]() ,
які випливають з того, що коли немає
циклів із від’ємною довжиною, вершинаk не
може бути внутрішньою в будь-яких
найкоротших шляхах, котрі починаються
чи закінчуються в самій вершині k.
Отже обчислюючи матрицю
,
які випливають з того, що коли немає
циклів із від’ємною довжиною, вершинаk не
може бути внутрішньою в будь-яких
найкоротших шляхах, котрі починаються
чи закінчуються в самій вершині k.
Отже обчислюючи матрицю
![]() ,
немає потреби переобчислювати елементиk–го
рядка й k–го
стовпця матриці
,
немає потреби переобчислювати елементиk–го
рядка й k–го
стовпця матриці
![]() .
Отже, у матриці
.
Отже, у матриці![]() за формулою (30.2) потрібно обчислювати
лишеn2
– 3n + 2
елементів. Очевидно, що складність
алгоритму Флойда-Уоршола становить
O(n3).
за формулою (30.2) потрібно обчислювати
лишеn2
– 3n + 2
елементів. Очевидно, що складність
алгоритму Флойда-Уоршола становить
O(n3).
Щоб після закінчення його
роботи можна було швидко знайти
найкоротший шлях між будь-якою парою
вершин, на k-й
ітерації разом із матрицею
![]() побудуємо матрицю
побудуємо матрицю![]() .
Спочатку беремо
.
Спочатку беремо![]() =i
для всіх і, j = 1, …, n,
ij;
=i
для всіх і, j = 1, …, n,
ij;
![]() = 0.
Далі, наk-й
ітерації візьмемо
= 0.
Далі, наk-й
ітерації візьмемо
![]() ,
якщо
,
якщо![]() ,
і
,
і![]() ,
якщо
,
якщо![]() .
Отже,
.
Отже,![]() – номер вершини, яка є перед вершиноюj у
поточному [i, j]–шляху,
тобто найкоротшому [i, j]–шляху,
усі вершини якого містяться в множині
{1, 2, …, k}.
Матриця
– номер вершини, яка є перед вершиноюj у
поточному [i, j]–шляху,
тобто найкоротшому [i, j]–шляху,
усі вершини якого містяться в множині
{1, 2, …, k}.
Матриця
![]() відіграє ту саму роль, що й вектор
в алгоритмі Дейкстри. За допомогою
матриці
відіграє ту саму роль, що й вектор
в алгоритмі Дейкстри. За допомогою
матриці
![]() вершини, через які проходить найкоротший
[i,
j] – шлях,
визначають так: i, ..,
j3, j2, j1, j,
де
вершини, через які проходить найкоротший
[i,
j] – шлях,
визначають так: i, ..,
j3, j2, j1, j,
де
![]() ,
,![]() ,
…
,
…
Розглянемо приклад. Потрібно знайти найкоротші шляхи між усіма вершинами в заданому на рис. 30.8 графі за допомогою алгоритму Флойда-Уоршола.

Рис 30.8.
Нижче наведемо результати виконання кожної з чотирьох ітерації алгоритму Флойда-Уоршола:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матриця
![]() дає
довжини найкоротших шляхів між усіма
парами вершин графу на рис. 30.8. Зокрема,
дає
довжини найкоротших шляхів між усіма
парами вершин графу на рис. 30.8. Зокрема,![]() ,
тобто довжина найкоротшого шляху від
вершини 3 до вершини 2 дорівнює –1. Для
знаходження самого шляху скористаємося
матрицею
,
тобто довжина найкоротшого шляху від
вершини 3 до вершини 2 дорівнює –1. Для
знаходження самого шляху скористаємося
матрицею![]() та запишемо у зворотному порядку вершини
через які він проходить:
та запишемо у зворотному порядку вершини
через які він проходить:![]() ,
,![]() ,
,![]() .
Останнє значення свідчить про те, що
найкоротший шлях з вершини 3 у вершину
4 йде безпосередньо з вершини 3, а отже
процедуру можна зупинити. Таким чином
отримали шлях: 3 – 4 – 1 – 2.
.
Останнє значення свідчить про те, що
найкоротший шлях з вершини 3 у вершину
4 йде безпосередньо з вершини 3, а отже
процедуру можна зупинити. Таким чином
отримали шлях: 3 – 4 – 1 – 2.
Очевидно, що як алгоритм Дейкстри, так і алгоритм Флойда-Уоршола можна застосовувати без жодних змін й до неорієнтованих графів. Для цього достатньо кожне ребро (u, v), що має вагу w(u, v), розглядати як пару дуг (u, v) та (v, u) з тією самою вагою. Слід ураховувати, що неорієнтоване ребро із від’ємною вагою одразу приводить до циклу із від’ємною довжиною, що робить алгоритм Флойда-Уоршола незастосовним.

 ;
; ;
; ;
; ;
; ;
;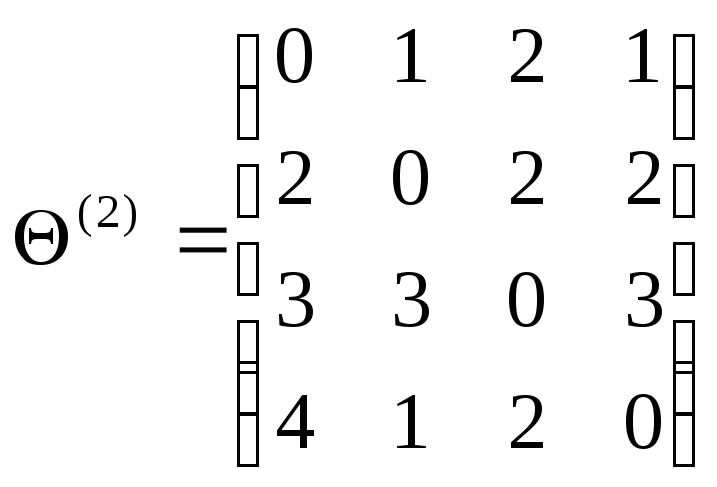 ;
;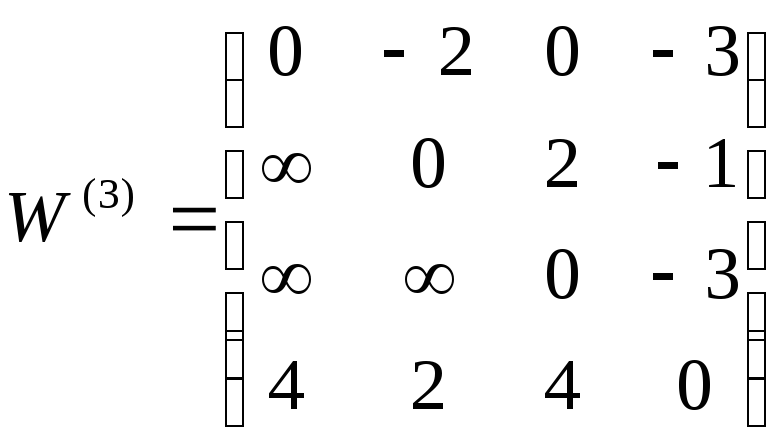 ;
; ;
; ;
;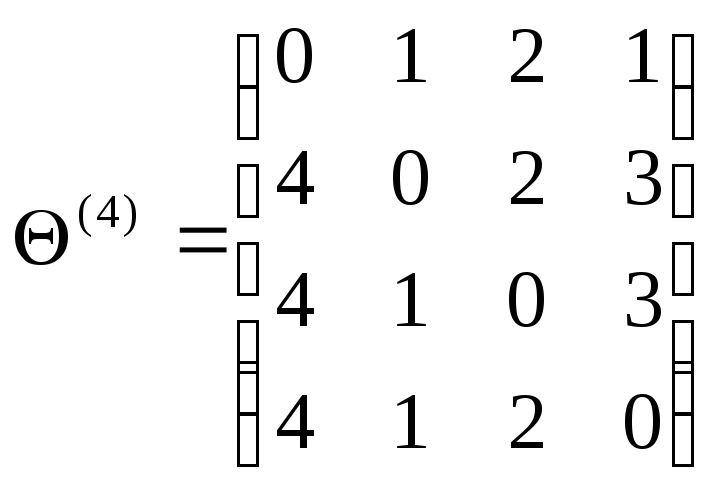 .
.