Вступительный экзамен 2018 / Раздел 14 (ответы)

Раздел 14. Комплексные числа.

1. Записать в алгебраической форме число:

Ответ:

2. Записать в алгебраической форме число:

Запишем число в тригонометрической форме:

Тогда искомое число равно:

Ответ:

3. Для числа найти и

Ответ:

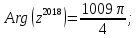
4. Записать в алгебраической форме число;

Для упрощения вычислений запишем числитель и знаменатель в показательной форме:

Ответ;

5. Нарисовать на комплексной плоскости область, заданную неравенствами:

Первое неравенство задает внутреннюю часть окружности с границей с радиусом 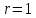и центром в точке .

Второе неравенство задает первую четверть комплексной плоскости (включая положительные полуоси).

Таким образом, система задает внутреннюю часть с границей расположенной в первой четверти половины окружности с центром в точке .

6. Нарисовать на комплексной плоскости область, заданную неравенством:

Представим число в алгебраической форме и решим неравенство:

7. Решить уравнение. Ответ записать в алгебраической форме

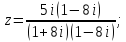
Ответ:

8. Решить уравнение. Ответ записать в алгебраической форме

Запишем комплексное число в алгебраической форме и решим уравнение:

Ответ:

9. Найти все решения уравнения , лежащие в области

Определим все корни уравнения:

Проверим принадлежность полученных корней заданной области:

Все решения уравнения лежат вне заданной области.

Ответ: в заданной области нет решений уравнения.

10. Найти все решения уравнения , лежащие в области

Определим все корни уравнения:

Проверим принадлежность полученных корней заданной области:

Ответ: