Вступительный экзамен 2018 / Раздел 10 (ответы)
.docxРаздел 10. Вычисление площадей плоских фигур.
-
Область ограничена кривыми:
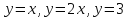 .
Найти ее площадь.
.
Найти ее площадь.
Найдем
точку пересечения кривых
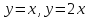 :
:
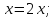
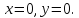
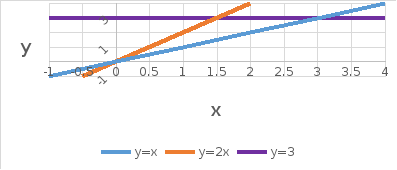
Для
кривых
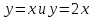 выразим
выразим
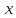 через
через
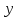 :
:
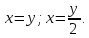
Площадь, ограниченная заданными кривыми равна:
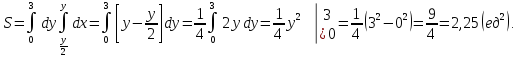
-
Область ограничена кривыми:
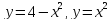 .
Найти ее площадь.
.
Найти ее площадь.
Найдем точку пересечения кривых:
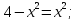
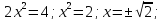
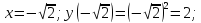
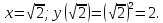
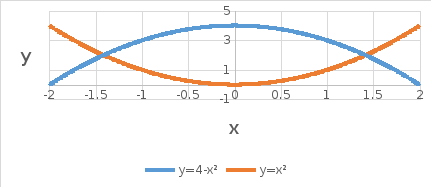
Площадь, ограниченная заданными кривыми равна:
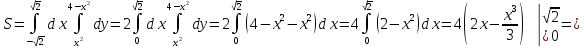
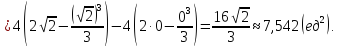
-
Область ограничена кривыми:
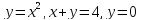 .
Найти ее площадь.
.
Найти ее площадь.
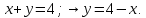
Найдем
точки пересечения кривых
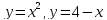 :
:
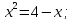
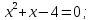
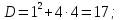
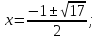
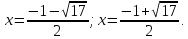
Найдем
точку пересечения кривой
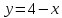 с
с
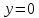 :
:
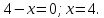
Найдем
точку пересечения кривой
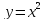 с
с
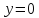 :
:
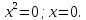
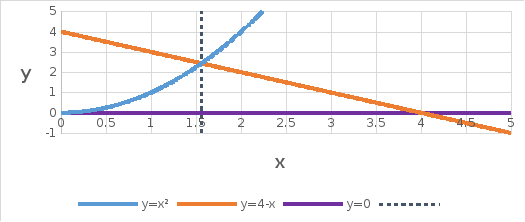
Площадь, ограниченная заданными кривыми равна:
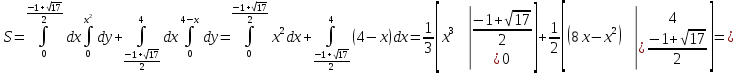
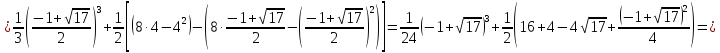
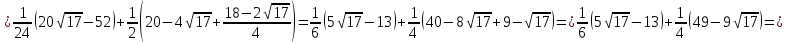
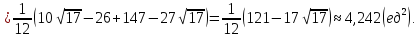
-
Область ограничена кривыми:
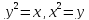 .
Найти ее площадь.
.
Найти ее площадь.
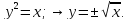
Найдем
точки пересечения кривых
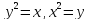 :
:
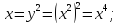
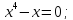
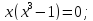
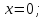
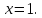
Определим
с какой из кривых
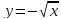 ,
,
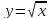 в точке
в точке
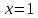 пересекается кривая
пересекается кривая
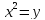 :
:
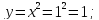
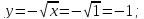
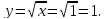
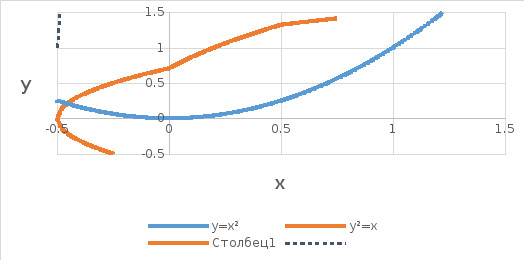
Площадь, ограниченная заданными кривыми равна:
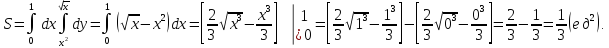
-
Найти площадь фигуры, если ее границей является кривая:
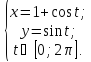
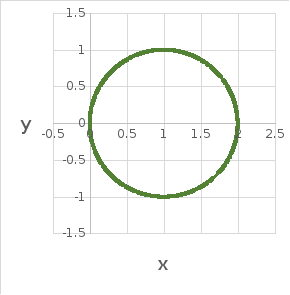 Определим
промежутки монотонности функции
Определим
промежутки монотонности функции
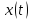 на интервале
на интервале
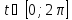 :
:
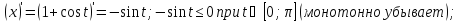
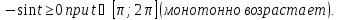
Определим
знак функции y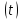 на интервале
на интервале
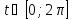 :
:
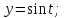
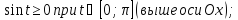
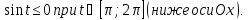
Найдем площадь по формуле:
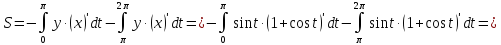
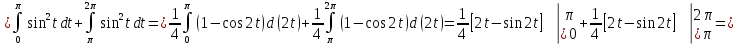
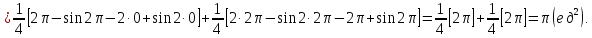
-
Найти площадь фигуры, если ее границей является кривая:
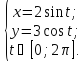
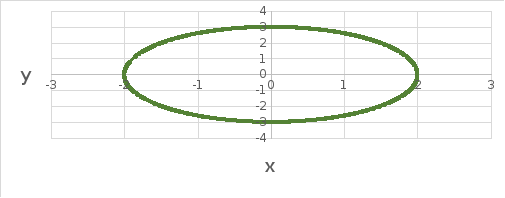
Найдем искомую площадь как умноженная на 4 площадь части фигуры, расположенной в первой четверти.
Определим
промежутки монотонности функции
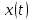 на интервале
на интервале
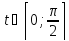 (в первой четверти):
(в первой четверти):
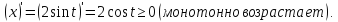
Определим
знак функции y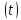 на интервале
на интервале
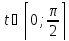 :
:
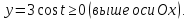
Найдем площадь по формуле:
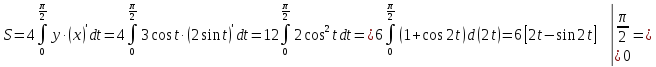
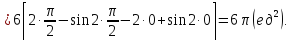
-
Найти площадь фигуры, если ее границей является кривая:
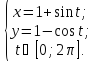
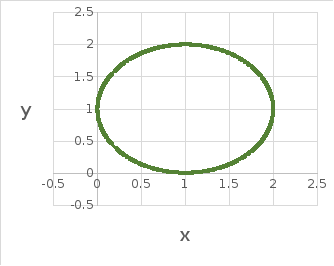
Определим
промежутки монотонности функции
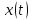 на интервале
на интервале
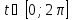 :
:
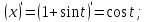
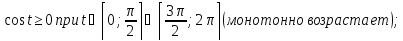
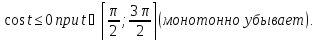
Определим
знак функции y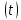 на интервале
на интервале
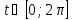 :
:
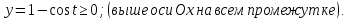
Найдем
площадь по формуле:
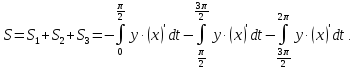
Примечание.
При определение
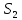 интеграл берется с минусом, т.к. на
интервале интегрирования функция
интеграл берется с минусом, т.к. на
интервале интегрирования функция
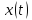 монотонно убывает. При определение
монотонно убывает. При определение
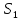 и
и
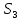 интеграл берется с минусом, т.к. они
представляют из себя площади пространства
ниже искомой фигуры (т.е. не входят в
искомую фигуру).
интеграл берется с минусом, т.к. они
представляют из себя площади пространства
ниже искомой фигуры (т.е. не входят в
искомую фигуру).
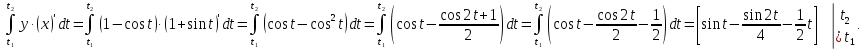
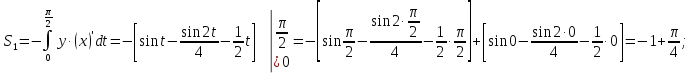
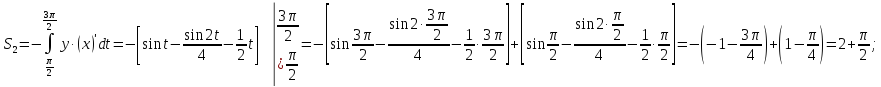
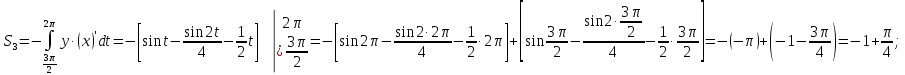
Искомая
площадь равна: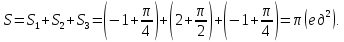
Ответ:
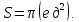
-
Найти площадь фигуры, ограниченной кривой, заданной в полярных координатах как
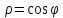
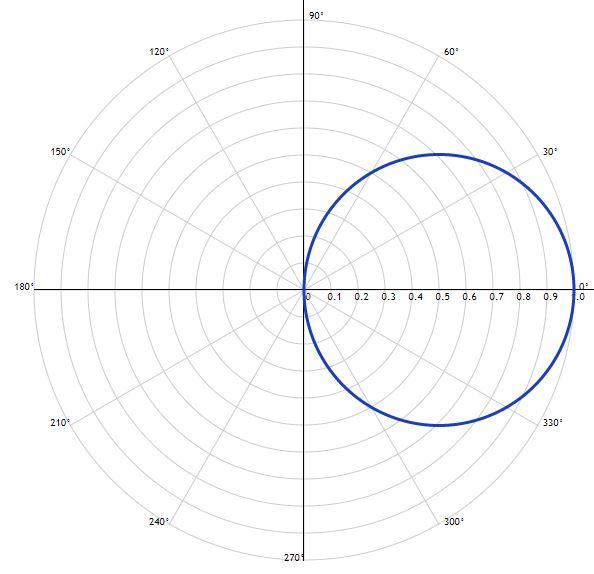
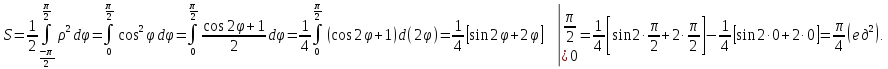
Ответ:
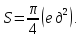
-
Найти площадь фигуры, ограниченной кривой, заданной в полярных координатах как
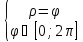
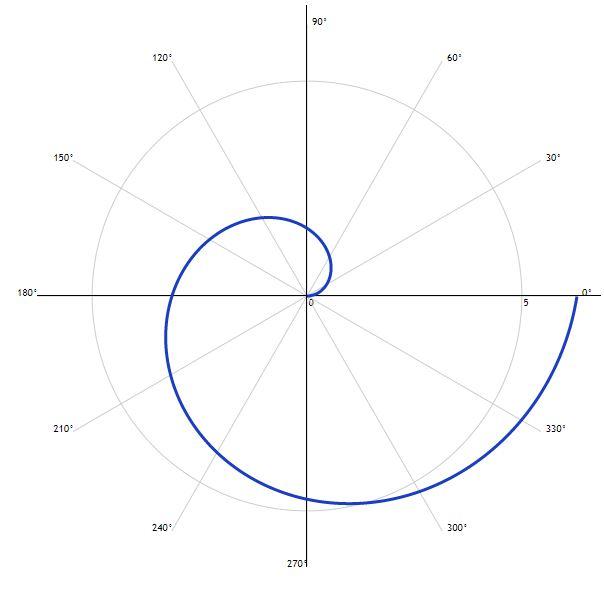
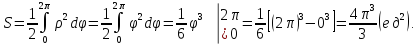 Ответ:
Ответ: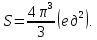
-
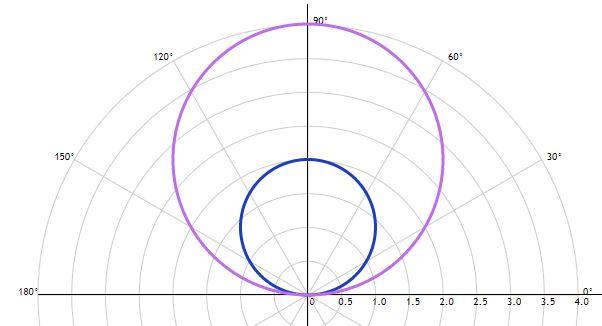
Найти площадь фигуры, ограниченной кривыми
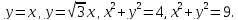
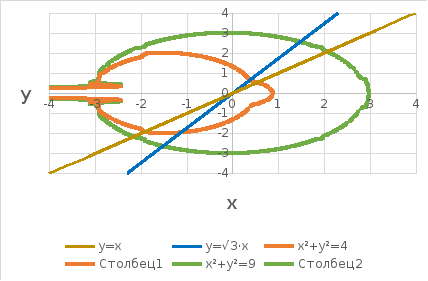
Так как заданные кривые представляют из себя две прямые и две окружности, для упрощения расчетов перейдем к полярным координатам:
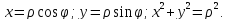
Кривая
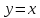 в полярных координатах имеет вид:
в полярных координатах имеет вид:
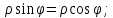
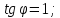
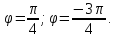
Кривая
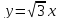 в полярных координатах имеет вид:
в полярных координатах имеет вид:
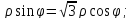
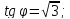
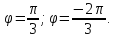
Кривая
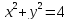 в полярных координатах имеет вид:
в полярных координатах имеет вид:
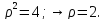
Кривая
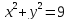 в полярных координатах имеет вид:
в полярных координатах имеет вид:
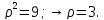
Пересечение заданных кривых образует кольцо, разделенное на 4 сектора. Таким образом условие задачи может подразумевать как нахождение площади двух противолежащих секторов меньшей площади, так и большей. Рассмотри оба случая.
Первый случай.
Фигура
ограничена кривыми:
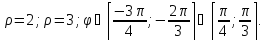
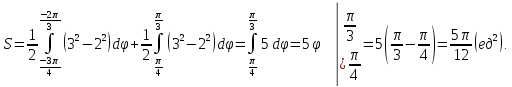
Второй
случай. Фигура ограничена кривыми:
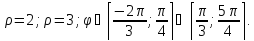
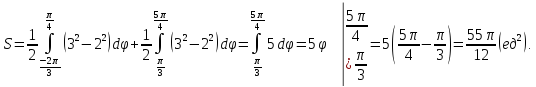
Ответ
:первый
случай (меньшие секторы кольца):
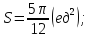 второй
случай (меньшие секторы кольца):
второй
случай (меньшие секторы кольца):
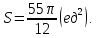
-
Найти площадь фигуры, ограниченной кривыми
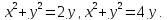
Перейдем
к полярным координатам:
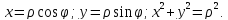
Кривая
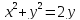 в полярных координатах имеет вид:
в полярных координатах имеет вид:
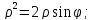
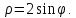
Кривая
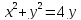 в полярных координатах имеет вид:
в полярных координатах имеет вид:
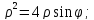
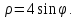
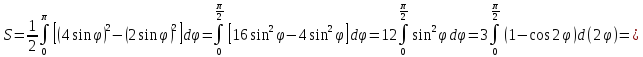
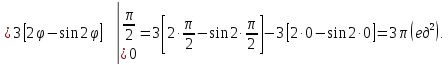 Ответ
Ответ