
Вступительный экзамен 2018 / Раздел 5 (ответы)
.docx-
Написать уравнение плоскости, проходящей через точку
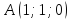
и
параллельной плоскости
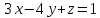
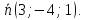
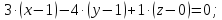
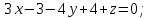
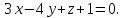
-
Написать уравнение плоскости, содержащей точку
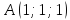 и ось Оx.
и ось Оx.
Возьмем две произвольные точки, лежащие на оси Ох:
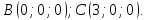
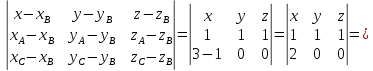
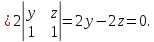
-
Найти угол между плоскостями
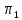 и
и
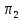 ,
где
,
где
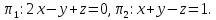
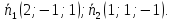
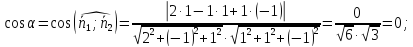
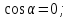
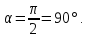
-
Написать каноническое уравнение прямой, проходящей через точки
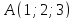 и
и
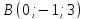 .
.
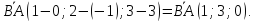
каноническое уравнение прямой:
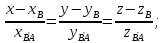
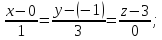
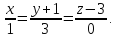
-
Найти угол между прямой
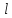 и плоскостью
и плоскостью
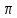 ,
где
,
где
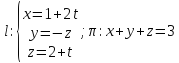
каноническому уравнению прямой:
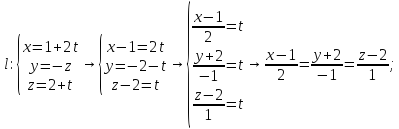
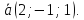
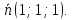
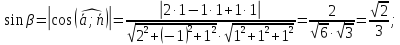
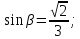
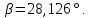
-
Написать параметрическое уравнение прямой, проходящей через
точку
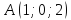 и перпендикулярной плоскости
и перпендикулярной плоскости
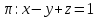 .
.
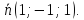
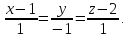
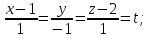
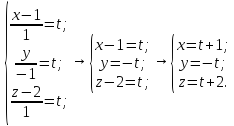
-
Написать каноническое уравнение прямой
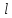 ,
которая является линией пересечения
,
которая является линией пересечения
плоскостей
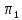 и
и
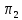 ,
где
,
где
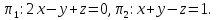
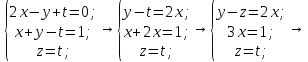
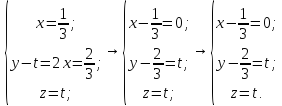
Таким
образом, получаем уравнение прямой
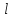 в каноническом виде:
в каноническом виде:
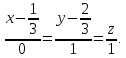
-
Найти угол между прямыми
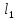 и
и
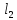 ,
где
,
где
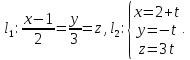
векторы
прямых
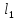 и
и
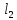 соответственно равны
соответственно равны
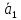 и
и
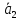 :
:
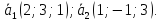
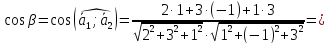
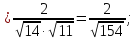
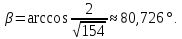
-
Лежат ли прямые
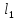 и
и
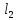 в одной плоскости, если
в одной плоскости, если
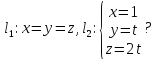
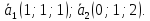
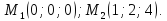
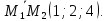
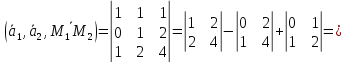
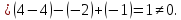
Ответ:
прямые
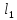 и
и
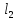 не
лежат в одной плоскости.
не
лежат в одной плоскости.
-
Лежат ли точки
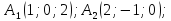
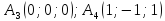 в одной плоскости?
в одной плоскости?
Найдем
уравнение плоскости, проходящей через
точки
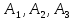
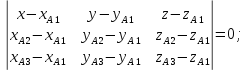
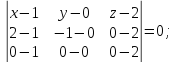
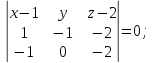
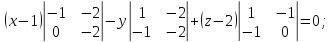
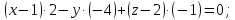
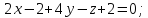
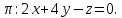
Проверим,
принадлежит ли точка
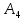 плоскости
плоскости
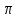 :
:
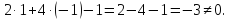
точки
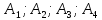 не
лежат в одной плоскости.
не
лежат в одной плоскости.
