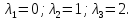Вступительный экзамен 2018 / Раздел 3(ответы)

Раздел 3. Матрица и определители

1. Пусть 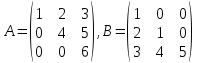. Найти определитель .

Найдем матрицу :

Определитель найдем разложением по первой строке:

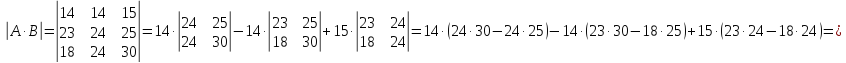
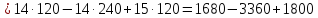=120.

Ответ:

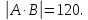
2. Найти обратную к матрице 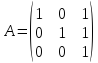. Сделать проверку.

Обратная матрица можно найти как:

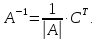
Определитель матрицы равен (по первому столбцу):

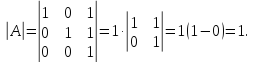
Найдем матрицу алгебраических дополнений:

Транспонированная матрица алгебраический дополнений равна:

Таким образом обратная матрица равна:

Проверка:

Обратная матрица найдена верно.

Ответ:

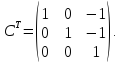
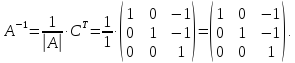
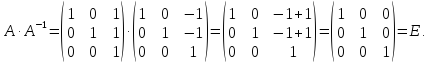
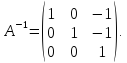
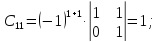
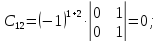
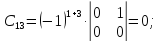
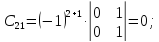
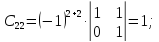
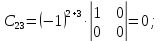
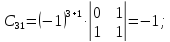
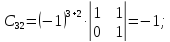
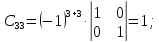
3. Решить матричное уравнение (с неизвестной матрицей ):

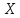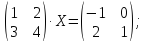
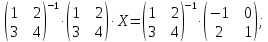
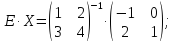
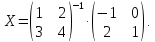
Найдем обратную матрицу :

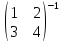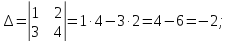
Матрица алгебраических дополнений равна:

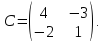
Транспонированная матрица алгебраических дополнений равна:

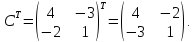
Обратная матрица равна

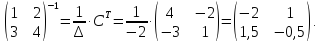
Тогда искомая матрица равна: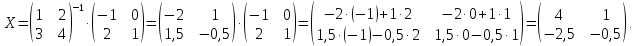

Ответ :

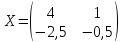
4. Найти определитель матрицы:

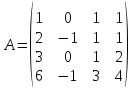
Найдем матрицу методом Гаусса. Приведем матрицу к ступенчатому виду:

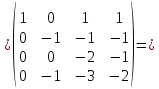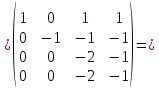{отнимем из 2-ой, 3-ьей и 4-ой строк первую умноженную на 2, 3 и 6 соответственно}{отнимем из 4-ой строки вторую}{отнимем из 4-ой строки третью}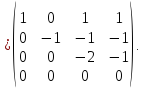У полученной матрицы четвертая строка нулевая, а значит ее определитель будет равен нулю. 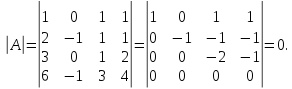Ответ: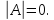

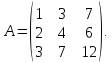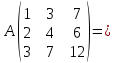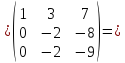5. Приведя матрицу к ступенчатому виду, найти ее определитель: Приведем матрицу к ступенчатому виду: {отнимем из 2-ой и 3-ьей строки первую умноженную на 2 и 3 соответственно}{отнимем из 3-ьей строки вторую}

Определитель равен произведению элементов главной диагонали матрицы, приведенной к ступенчатому виду:

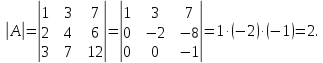
Ответ:

6. Определить ранг матрицы

Приведем заданную матрицу к ступенчатому виду:{отнимем из 2-ой, 3-ьей и 4-ой строк первую умноженную на 4, 3 и 8 соответственно}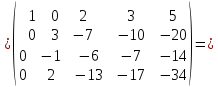{прибавим к 3-ьей строке вторую разделенную на 3; отнимем из 4-ой строки вторую умноженную на 2/3}

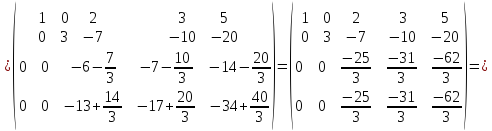{отнимем из 4-ой строки третью}

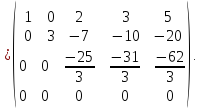
Таким образом ранг заданной матрицы равен:

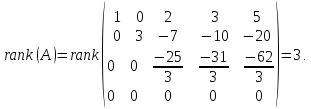
Ответ:

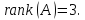
7. Пусть 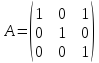. Найти .

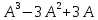Возведем заданную матрицу во вторую степень, для этого умножив матрицу 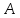саму на себя:

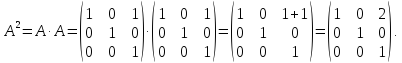
Возведем заданную матрицу в третью степень, для этого умножив матрицу 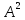на :

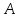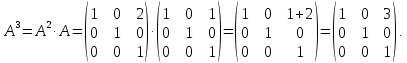
Найдем квадрат матрицы 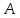, умноженной на 3:

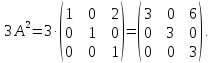
Найдем произведение матрицы 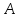на 3:

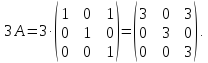
Тогда искомое выражение равно:

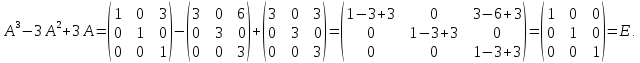
Ответ :

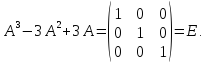
8. Приведя матрицу 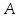к ступенчатому виду, определить ее ранг:

Приведем заданную матрицу к ступенчатому виду:

{отнимем из 3-ьей и 4-ой строк первую}{отнимем из 4-ой строки третью}

Таким образом ранг заданной матрицы равен:

Ответ:

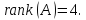
9. Найти определитель 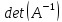обратной матрице , если

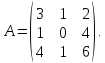
Определитель заданной матрицы равен (разложением по первой строке):

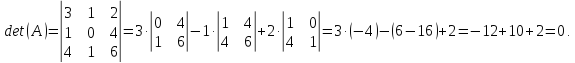
Так как определитель матрицы 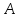равен нулю, то обратной матрицы 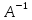не существует.

Ответ:

обратная матрица 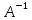не существует.

10. Найт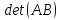и , если .

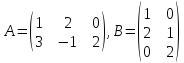Найдем произведение матрицы 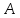на матрицу :

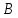Определитель матрицы 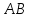равен:

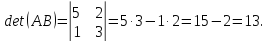
Ответ: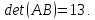

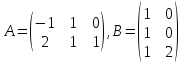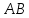11. Пусть . Имеет ли матрица обратную?

Найдем произведение матрицы 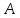на матрицу :

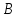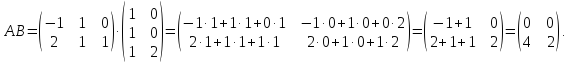
Определитель матрицы 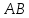равен

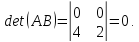
Матрица 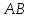не имеет обратную, так как ее определитель равен 0.

Ответ: матрица 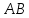не имеет обратную.

12. Найти собственные числа матрицы

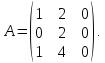
Найдем собственные числа из характеристического уравнения заданной матрицы:

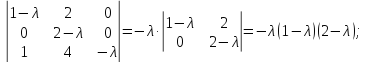
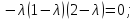
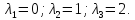
Ответ: