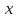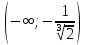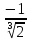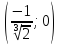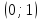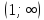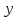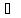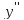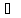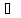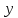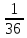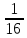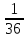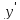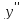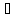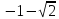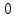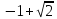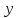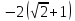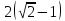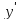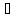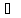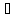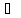1.1 Найдем область определения функции.

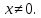
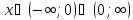
1.2 четность/нечетность:

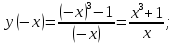
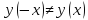и

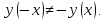
1.3 Функция не является периодичной

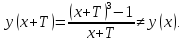
1.4 Наличие асимптот, предел слева для

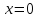
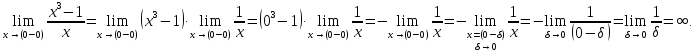
Найдем предел справа для

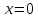
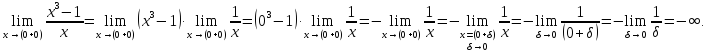
Наличие горизонтальных асимптот пр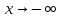и и

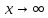
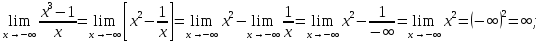
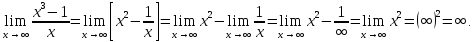
Наклонных асимптот при , (

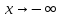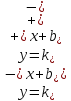
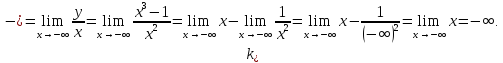
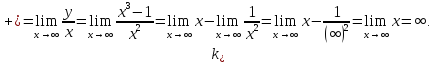
1.5 Определим точки пересечения функции с осью абсцисс (Оx)

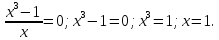
1.7 Промежутки знакопостоянства.

.

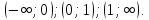
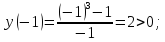
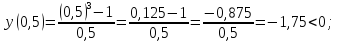
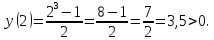
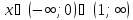1.8 Определим экстремумы функции и промежутки возрастания/убывания функции:

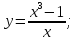
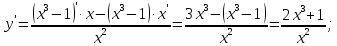
						1
	+		+		-	0	+
		Точка минимума		Вертикальная асимптота		Пересечение с осью Ох

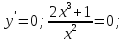
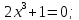
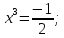
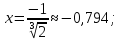
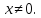
Знак производной на каждом из трех промежутков:

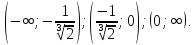
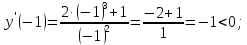
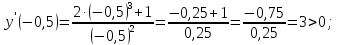
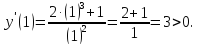
убывает при 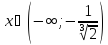и возрастает при 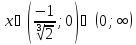. Точка

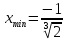
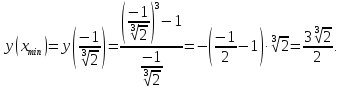
Определим точки перегиба и промежутки выпуклости/вогнутости функции

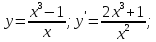
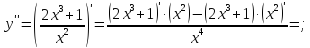
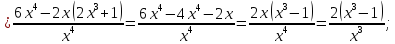
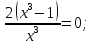
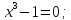
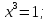
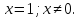
Знак второй производной на каждом из трех промежутков:

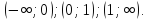
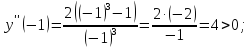
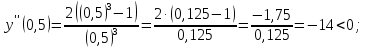
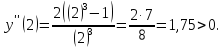
2)

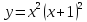
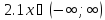
2.2 Проверим функцию на четность/нечетность

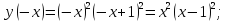
Заданная функция является функцией общего вида, так как не выполняются условия четности и нечетност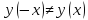и:

и

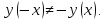
2.3 Функция не является периодичной

2.4 Исследуем функцию на точки разрыва и наличие асимптот

Так как область определения 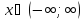, то функция не имеет точек разрыва.

Проверим наличие горизонтальных асимптот пр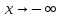и и

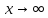
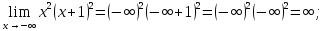
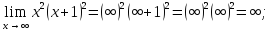
Так как оба предела не являются конечными, то пр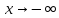и и 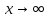горизонтальных асимптот не существует.

Проверим наличие наклонных асимптот при 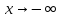, где уравнение асимптоты имеет вид

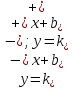
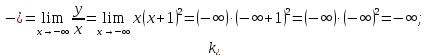
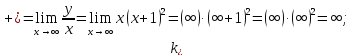
2.5 Определим точки пересечения функции с осью абсцисс (Оx)

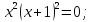
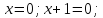
										0
	+	0	+		+		+		+	0	+
		Пересечение с осью Ох. Точка минимума		Точка перегиба		Точка максимума		Точка перегиба		Пересечение с осями Ох и Oy. Точка минимума

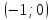Функция пересекается с осью абсцисс в точках и .

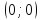2.6 Определим точки пересечения функции с осью ординат (Оy)

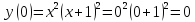
Функция пересекается с осью абсцисс в точке .

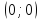2.7 Определим промежутки знакопостоянства.

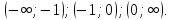
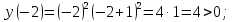
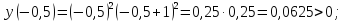
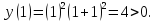
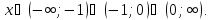
2.8 Определим экстремумы функции и промежутки возрастания/убывания функции

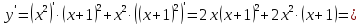
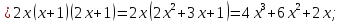
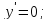
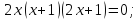
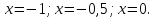
Определим знак производной на каждом из четырех промежутков:

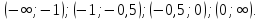
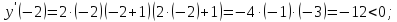
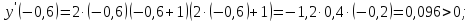
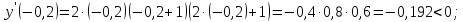
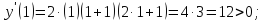
Таким образом функция убывает при 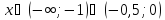и возрастает при .

В этих точках функция принимает значения:

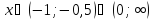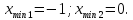
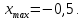
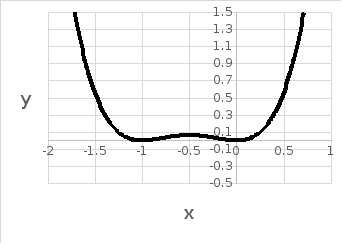
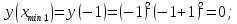
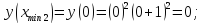
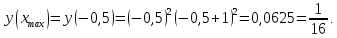
2.9 Точки перегиба и промежутки выпуклости/вогнутости функции

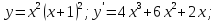
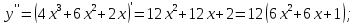
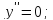
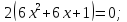
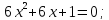
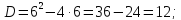
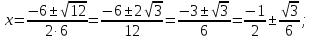
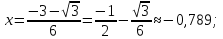
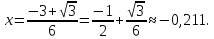
Определим знак второй производной на каждом из трех промежутков:

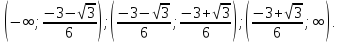
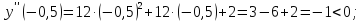
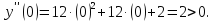
Таким образом функция выпуклая вверх при 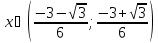и выпуклая вниз (вогнутая) при .

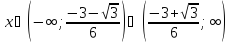Точк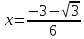и и 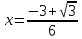являются точками перегиба функции. В этих точках функция принимает значения:

;

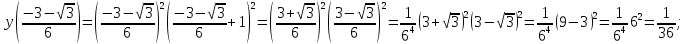
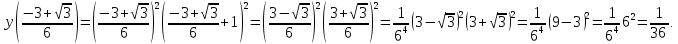
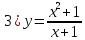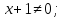
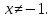
1) Область определения

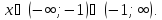
2) Проверим функцию на четность/нечетность

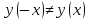и

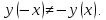
3.3 Функция не является периодичной

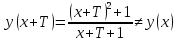
3.4 Исследуем функцию на точки разрыва и наличие асимптот

Найдем предел слева для

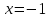
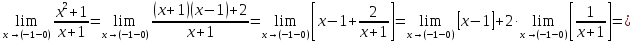
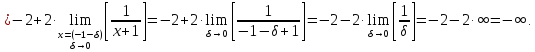
Найдем предел справа для

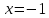
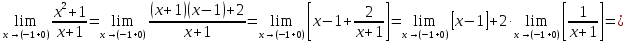
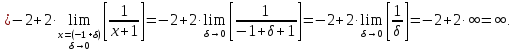
Таким образом в точке 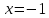функция терпит разрыв второго рода; также 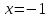является вертикальной асимптотой.

Проверим наличие горизонтальных асимптот пр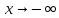и и

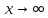
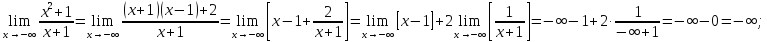
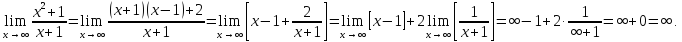
Проверим наличие наклонных асимптот при 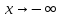, где уравнение асимптоты имеет вид

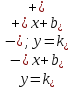
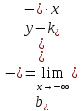
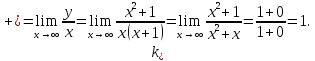
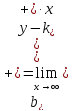
	-		-		+	1	+		+
		Точка максимума		Вертикальная асимптота		Пересечение с осью Оy		Точка минимума
	Наклонная асимптота y=x-1								Наклонная асимптота y=x-1

3.5 Определим точки пересечения функции с осью абсцисс (Оx)

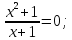
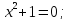
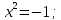
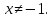
Функция не пересекается с осью абсцисс.

3.6 Определим точки пересечения функции с осью ординат

(Оy)

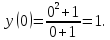
3.7 Определим промежутки знакопостоянства.

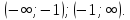
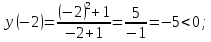
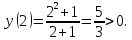
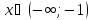и выше при .
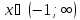