
Вступительный экзамен 2018 / Задание
.pdf
|
|
|
sin z |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
||||||
5) |
|
|
|
|
|
dz |
; |
|
6) |
|
|
|
|
|
|
|
|
; |
|||||
|
z cos z |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
(x2 |
4)2 |
|
|||||||||||||||||||
|
|z| 1 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
xsin 2x |
|
|
|
|
2 |
|
|
dx |
|
|
|
|
|
|||||||||
7) |
|
|
|
|
|
dx ; |
8) |
|
|
|
|
|
|
|
|
; |
|
||||||
|
x |
2 |
9 |
cos x 2 |
|
||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
dx |
|
|
|
|
x cos x |
|
|
|
|||||||||
9) |
|
|
|
|
|
|
|
|
|
|
; |
10) |
|
|
|
|
|
|
dx . |
||||
|
(x |
2 |
1)(x |
2 |
|
x |
2 |
1 |
|||||||||||||||
|
|
|
|
9) |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Раздел 18. Функция-оригинал и ее изображение по Лапласу.
1) |
Найти изображение функции f (t) t2e 3t . |
|
||||
2) |
Найти изображение функции f (t) te 3t sin 2t . |
|
||||
3) |
Найти изображение функции f (t) t ch 2t sh t . |
|
||||
|
|
|
|
|
t |
|
4) |
Найти изображение функции f (t) e x cos(t x) dx . |
|
||||
|
|
|
|
|
0 |
|
5) |
Пусть |
f (t) e |
2t |
sin 3t . Найти изображение функции |
|
|
|
f (t) . |
|||||
|
|
|
|
|
t |
|
6) |
Найти изображение функции f (t) x3e 3xdx . |
|
||||
|
|
|
|
|
0 |
|
7) |
Пусть |
f (t) 3, |
t [0;1], |
Найти изображение f (t) . |
|
|
|
|
0, |
t [0;1]. |
|
|
|
|
|
0, |
t 0, |
|
|
|
|
|
|
t [0;1], |
|
|
|
|
|
|
t, |
|
|
|
8) |
Пусть |
f (t) 1, |
t [1;2], |
. Найти изображение f (t) . |
|
|
|
|
|
t 2. |
|
|
|
|
|
0, |
|
|
||
9) Пусть (t) 0, |
t 0, Найти изображение функции |
f (t) (t 1)e(t 1) (t 1) . |
||
|
1, |
t 0. |
|
|
10) |
Пусть (t) 0, |
t 0, Найти изображение f (t) sin 2(t 2)et 2 (t 2) . |
||
|
1, |
t 0. |
|
|
11) |
Найти изображение функции f (t) t sin2 2t . |
|
||
Раздел 19. Восстановление оригинала по изображению.
Найти (непрерывную на [0; ) ) функцию-оригинал, если ее изображение F ( p) равно:
|
F ( p) |
p2 |
2) |
F ( p) |
p 3 |
; |
|
1) |
|
; |
|
||||
|
p2 6 p 10 |
||||||
( p2 1)( p2 2) |
|||||||
|
|
|
|
11 |
|
|
|
|
|
|
|
|
p 2 |
|
|
|
|
|
|
|
|
|
p |
|
|
|||||||||
3) |
F ( p) |
|
|
|
|
|
; |
4) |
F ( p) |
|
|
|
; |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
4 p |
5 |
|
|
|
2 |
9 |
|
||||||||||||||||
|
|
p |
|
|
|
|
|
p |
|
|
|
|
|
|||||||||||||
|
|
|
|
dq |
|
|
|
|
|
|
|
e 2 p |
|
|
|
|
|
|
||||||||
5) F ( p) |
|
|
; |
|
|
|
6) |
F ( p) |
|
; |
|
|
|
|
||||||||||||
q2 4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
p 1 |
|
|
|
|
|||||||||||||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
dq |
|
|
|
||||
7) F ( p) (e 2 p 3e p ) |
; |
8) |
F ( p) |
|
|
|
|
|
|
; |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
p |
|
q(q2 |
1) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||
9) F ( p) |
|
|
; |
|
|
|
|
|
10) F ( p) |
|
|
; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
p |
k 1 |
|
|
|
|
|
(2 p) |
k 1 |
||||||||||||||||||
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
||||||||||
Раздел 20. Операционные методы решения дифференциальных уравнений и систем дифференциальных уравнений.
1)Решить операционным методом задачу Коши: x x 2t 3, x(0) 1, x (0) 1.
2)Решить операционным методом задачу Коши: x x t , x(0) 1, x (0) 0 .
3) Решить операционным методом задачу Коши:
|
t |
|
|
|
|
|
|
|
x |
x 2e , |
x(0) 0 , x (0) 1. |
|
|
|
|
||
4) Решить операционным методом задачу Коши: |
|
|
|
|
||||
|
x 2cost , |
|
|
|
|
|
|
|
x |
x(0) x (0) 0 . |
|
|
|
|
|||
5) Операционным методом найти решение системы уравнений |
|
|
|
|||||
x y 0 |
||||||||
|
|
|
|
|
|
y x 1, |
||
удовлетворяющее начальным условиям x(0) 2 , |
y(0) 1. |
|
|
|
||||
|
|
|
|
|
|
x 2 y 2t |
||
6) Операционным методом найти решение системы уравнений |
|
1 |
|
|||||
|
|
|||||||
|
|
|
|
|
|
y |
|
x 1, |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
удовлетворяющее начальным условиям x(0) 2 , |
y(0) 1. |
|
|
|
||||
7) Операционным методом найти решение системы уравнений |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
x 2 y 0 |
|
удовлетворяющее начальным условиям x(0) 2 |
, y(0) 1. |
|||||
|
|
2t |
|
|||||
y x 3e |
|
1, |
|
|
|
|
|
|
12

Решения |
|
|
|
|
|
|
|
|
|
||||
§1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
f ' x |
1 |
(2 (tg x)5 ) 2/3 ( 5(tg x)4 ) |
1 |
|
|
|
5(tg x)4 |
|
. |
|||
|
cos2 |
|
|
|
|
||||||||
|
|
|
|
||||||||||
|
|
|
3 |
|
|
x |
33 (2 (tg x)5 )2 cos2 x |
|
|
||||
§2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
y |
x3 1 |
. |
|
|
|
|
|
|
|
|
||
|
x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
1. ОДЗ: x 0. |
|
|
|
|
|
|
|
|
|||||
|
lim |
|
f (x) |
|
|
|
|
|
|
|
|
||
2. |
x 0 0 |
|
|
|
x 0 – вертикальная асимптота. |
|
|
||||||
|
|
|
|
|
|
|
|||||||
|
lim |
|
f (x) |
|
|
|
|
|
|
|
|
||
|
x 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
3.f ( x) f (x), f ( x) f (x) , периода нет, т.е. функция общего вида.
4.y 0 x3 1 0 x 1; точка (1;0) – точка пересечения с осью Оx.
5.Найдем наклонные (горизонтальные) асимптоты:
k lim |
|
f (x) |
lim |
x3 |
1 |
, т.е. наклонных и горизонтальных асимптот нет. |
||||||||||||||||||
|
|
x |
x2 |
|
|
|||||||||||||||||||
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
3 |
|
1 |
|
|
|
2 |
x (x |
3 |
1) |
|
2x |
3 |
1 |
|
||||||||
|
|
|
|
3x |
|
|
|
|
||||||||||||||||
6. |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
x |
|
|
|
|
|
x |
2 |
|
|
x |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y 0 2x3 1 0 x 312 ; y x2 0 x 0.
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
, |
т.е. |
|
|
|
|
|
; |
|
|
|
|
|
|
– точка минимума. |
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
3 2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
4 |
|
|
|
|
|
3 2 |
|
|
|
|
3 4 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2x |
3 |
|
|
|
|
|
|
|
|
2 |
x |
2 |
(2x |
3 |
1)2x |
|
|
|
2x |
4 |
2x |
|
2(x |
3 |
1) |
|
|||||||||||||||||||
7. |
|
y ' |
|
1 |
|
6x |
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
x |
4 |
|
|
x |
3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
y 0 x3 1 0 x 1. y x3 0 x 0.
13

|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
3 |
|
|
|
3 |
|
|
1 |
|
|
|
3 |
|
|||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
3 |
2 |
|
|
|
|
|||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, т.е. |
|
|
|
; |
|
|
|
|
|
– точка минимума. |
||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|||||||||||||
|
|
3 |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
3 4 |
|
|
2 |
|
|
|
4 |
|
|||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y(1) 0 , т.е. точка (1;0) – точка перегиба.
§3.
|
1 |
0 |
1 |
2) A 0 |
1 |
1 . |
|
|
0 |
0 |
|
|
1 |
||
1. | A | 1 0 !A 1. |
|
||||||||
|
A 1 |
A |
0 |
|
A |
1 |
|||
2. |
A11 |
0 |
A21 |
1 |
|
A31 |
1 |
||
|
A12 |
0 |
A22 |
0 |
|
A32 |
1 |
||
|
13 |
|
|
23 |
|
|
33 |
|
|
|
|
1 |
0 |
1 |
|
|
|||
3. |
AT 0 |
1 |
1 . |
|
|||||
|
|
|
0 |
1 |
|
|
|
||
|
|
0 |
|
|
|
||||
|
A 1 |
1 |
|
|
|
1 |
0 |
1 |
|
4. |
|
AT |
0 |
1 |
1 . |
||||
|
|
||||||||
|
|
| A | |
|
0 |
0 |
|
|||
|
|
|
1 |
||||||
5. Проверка: AA 1 A 1 A E (?)
14

1 |
0 |
1 1 |
0 |
1 |
1 |
0 |
0 |
AA 1 0 |
1 |
1 0 |
1 |
1 |
0 |
1 |
0 . |
|
0 |
|
0 |
|
|
0 |
|
0 |
1 0 |
1 |
0 |
1 |
|||
A 1 A E. |
|
|
|
|
|
|
|
§4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) 2x1 4x2 2x4 16, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x |
2x |
|
|
3x 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A | B |
2 |
|
|
|
|
|
1/ 2 |
|
1 2 0 1 |
|
|
|
|
|
|
|
|
||||||||||||||
|
4 0 2 |
16 |
|
|
|
8 |
|
|
|
|
|
||||||||||||||||||||
|
1 |
|
|
0 2 3 |
|
2 |
|
|
|
|
1 0 2 3 |
|
2 |
|
|
|
|
|
|
||||||||||||
|
1 2 |
|
|
0 1 |
|
8 |
|
1 |
|
|
1 |
2 0 |
1 |
|
8 |
|
2 |
1 |
0 2 3 |
|
2 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
0 2 2 4 |
|
6 |
|
1/ 2 |
|
|
0 0 1 2 |
|
3 |
|
|
0 1 1 2 |
|
3 |
|
|||||||||||||||
Rg A Rg A | B 2; dim L 2 ФСР: e1, e2. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2 баз. переменные: x1, x2 , 2 своб. переменные: x3 , x 4 . |
|
|
|
|
|
||||||||||||||||||||||||||
x1 |
2 2x3 |
3x4 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
3 x |
|
2x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
2 2x3 |
3x4 |
|
2 |
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|||||||||||||
|
x2 |
|
|
3 x3 2x4 |
|
3 |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||
xî .í . x |
|
|
|
|
x |
|
|
|
|
|
0 |
|
C1 |
1 |
C2 |
|
0 |
. |
|
|
|
|
|
||||||||
|
|
3 |
|
|
3 |
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
x4 |
|
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x÷.í . |
|
|
e1 |
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
Проверки: x÷.í . : 2 ( 2) 4 3 2 0 16; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
e1 : 2 ( 2) 4 ( 1) 2 0 0; e2 : 2 ( 3) 4 ( 2) 2 1 0.
§5.
1) |
A(1;1;0), : 3x 4y z 1, A и . Так как , то n1 n2 , n1 |
{3; 4;1} – |
||
|
нормальный вектор плоскости , который можно взять за нормальный вектор |
|||
|
к плоскости точка A , тогда уравнение плоскости : |
|
|
|
|
A(x x0 ) B( y y0 ) C(z z0 ) 0, |
|
|
|
т.е. 3(x 1) 4( y 1) 1(z 0) 0 , : 3x 4y z 1 0. |
|
|
|
|
§6. |
|
|
|
|
1) |
(x 5)2 y2 3– окружность с центром в точке ( 5;0) и радиусом |
|
|
|
3. |
||||
§7.
15

7) ln xdx ?
Интегрирование по частям:
udv uv vdu  u ln x, du 1x dx
u ln x, du 1x dx x ln x dx x(ln x 1) C. dv dx, v x
x ln x dx x(ln x 1) C. dv dx, v x
§8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6) |
sin2 x cos x dx sin2 |
x d (sin x) |
sin3 x |
|
C (метод подведения под знак диффе- |
|||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ренциала). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
§9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) dx F (b) F (a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
dx |
|
|
e |
d (ln x) |
|
1 |
|
|
|
e |
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
. |
||||||
2 x ln |
3 |
|
2 |
|
3 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
||||||||||
|
|
x |
|
ln |
|
x |
|
2ln |
|
x |
|
2 |
|
|
2ln |
|
2 |
|
2ln |
|
e |
|
2 |
|
|
ln |
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
§10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
y x; y 2x; y 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
3/2 |
|
|
|
|
|
|
|
3 |
|
|
|
x |
2 |
|
|
3/2 |
|
|
x |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Sф игуры |
|
(2x x)dx (3 x)dx |
|
|
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
3/2 |
|
|
2 |
|
|
0 |
|
2 |
|
|
3/2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
9 |
9 |
9 |
|
9 |
|
9 |
|
9 |
2 |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
8 |
|
|
2 |
2 |
8 |
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
§11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
n 1 |
3n 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1. Проверить необходимое условие сходимости: lim |
|
1 |
0. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
3n 4 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
n |
|
1 |
|
|
|
2. По второй теореме сравнения |
|
|
|
расходится; так как lim |
|
|
|
, то |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
3n 4 1 3 |
|
|||||||
оба ряда ведут себя одинаково, т.е. исходный ряд расходится.
16

§12. |
|
|
|
|
|
|
|
|
|
|
|||
1) |
|
xy x, |
|
|
|
|
|
|
|
||||
y |
|
|
|
|
|
|
|
||||||
|
dy |
x( y 1) |
|: y 1 0, |
|
|
|
|
|
|||||
|
dx |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dy |
|
xdx, |
|
|
|
|
|
|
|
|||
|
y 1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
dy |
|
|
|
x2 |
|
|
x2 |
/2 |
x2 /2 |
||
|
xdx; |
ln | y 1| |
|
C; |
y 1 e |
|
C; y e |
C 1; так как при C 0 |
|||||
y 1 |
2 |
|
|||||||||||
y 1, то ответ: y ex2 /2C 1.
§13.
1) y 3y 2y 0.
Составим характеристическое уравнение:
3 3 2 |
2 0, |
( 2 |
3 2) 0, |
0, |
|
1, |
2 – все корни кратности 1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y C C ex |
C |
2 x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
o.o. |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
§14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
i sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i 9 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
cos |
i sin |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
9 |
|
|
9 |
|
|
e |
|
|
|
|
|
i |
|
|
|
3 1 i. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
4) 5б: |
|
|
|
|
|
|
e |
9 |
18 |
e |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
5 |
i sin |
|
5 |
|
|
|
|
i |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
6 2 2 |
|
|||||||||||||||||||||||||||
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
e |
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
18 |
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
§15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z3 i z | z | ei ; i ei |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
1, |
|
|
|
|
|
|
|
|
|
|
|
| z | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| z | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
| z |3 ei3 1 e |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2 k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i sin i; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
k 0 |
z 1 ei 2 |
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
k 1 |
z 1 e 2 |
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
i sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
; |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
k 2 |
z 1 e 2 |
|
|
|
|
cos |
|
|
|
|
|
|
|
i sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
. |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
||||||||||||||||
§16. sinz z .
17

z 0 – устранимая точка, lim |
|
z |
|
|
0; |
|
|
z |
k при k , 2 , |
|
– полюса 1-го |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
sin z |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
порядка, так как |
1 |
|
|
sin z |
|
имеет в этих точках нуль первого порядка ( |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
f |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
sin k 0, cos k 0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
§17. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
z3 sin |
1 |
dz 0, так как разложение в ряд Лорана этой функции имеет вид: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|z| 1 |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
1 |
|
|
|
|
|
3 |
|
1 |
|
|
1 |
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
z |
|
sin |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
z |
|
|
, |
т.е. коэффициент при сте- |
||||||||||||||||||||||||||||||
|
z |
|
|
3! |
|
z |
3 |
5! |
z |
5 |
|
|
6 |
5! |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
пени |
1 |
|
равен 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
§18. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1) 5б: так как e 3t |
|
|
|
|
|
|
1 |
|
|
|
|
, |
|
а домножение оригинала на ( t) соответствует диф- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
p 3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3t |
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
||||||||
|
|
ференцированию изображения, то t |
|
|
e |
|
|
|
|
|
|
|
|
(( p |
3) |
|
|
|
|
3 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
3 |
|
|
|
|
|
|
|
|
|
|
( p |
3) |
|
|
|||||||
§19. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
tk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
F ( p) |
|
|
|
. |
Так как |
|
|
|
|
|
|
|
|
|
|
|
, то F ( p) |
|
|
et . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
p |
k 1 |
|
|
|
p |
k 1 |
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
§20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
t |
|
|
x(0) 0; |
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x |
x 2e , |
|
|
|
x (0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p( pF( p) |
|
|
|
|
|
|
|
|
|
|
|
p |
2 |
F( p) 1; |
|
|
|
|
|||||||||||||||||||||
Пусть x(t) F( p). Тогда x (t) |
x(0)) x (0) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
et |
|
1 |
|
|
p2 F ( p) 1 F ( p) 2 |
|
|
1 |
|
|
( p2 1)F( p) |
2 |
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
p 1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
F ( p) |
|
|
|
|
|
|
p 1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
p |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
( p 1)( p2 |
1) |
|
p 1 |
p2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Так как F( p) et |
cost, |
то ответ x(t) et |
cost. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
18

Справочные материалы
A. Таблица производных
Б. Таблица интегралов
19
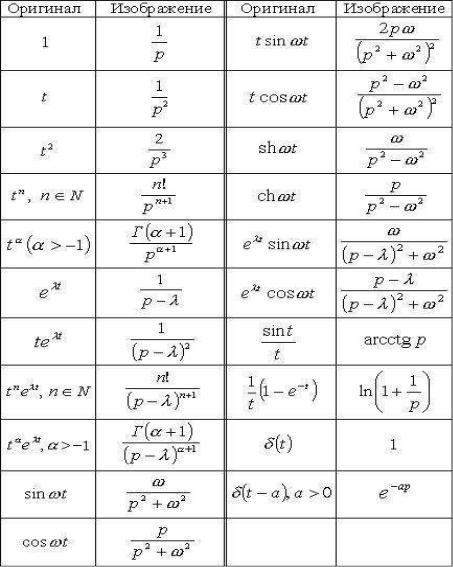
В. Таблица изображений и оригиналов
20
