Учебный вопрос №3 «Определение по карте абсолютных высот и взаимного превышения точек, определение крутизны скатов».

Высоты точек местности по карте определяют по горизонталям, используя имеющиеся на ней высотные отметки.

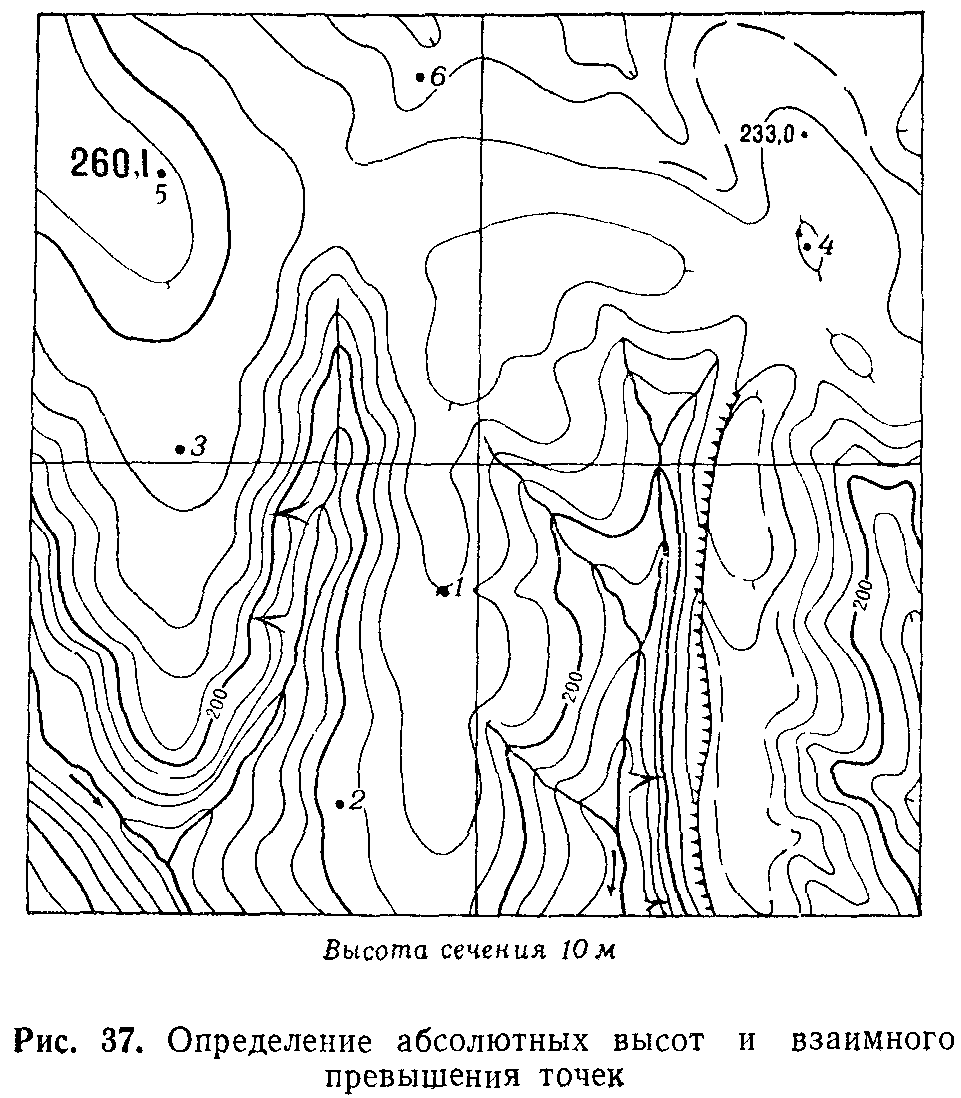
Если определяемая точка расположена на горизонтали, то ее абсолютная высота, очевидно, равна высоте этой горизон­тали. Если же точка находится между горизонталями, то надо определить отметку ближайшей к ней нижней горизонтали и при­бавить к этой отметке превышение данной точки над горизонта­лью. Это превышение определяется на глаз. Например, (рис. 37), абсолютная высота точки 1 будет 230 м, так как горизонталь, на которой она расположена, лежит на три высоты сечения выше го­ризонтали с отметкой 200 м. Высота точки 2 равна 205 м: она расположена посредине между горизонталями, одна из которых имеет высоту 200 м (утолщенная горизонталь), а другая 210 м. Точки 3 и 4 имеют примерно одну и ту же высоту – 242 м.

Превышение одной точки над другой определяется как раз­ность их абсолютных высот. Если же точки расположены на одном и том же скате, то задача решается просто путем подсчета числа промежутков между горизонталями этих точек: превышение между ними равно произведению высоты сечения на полученное число промежутков между горизонталями. Например, точка 5 на рис. 37 расположена выше точки 6 на 45 м (4,5 промежутка между гори­зонталями) и выше точки 2 на 55 м.

Точность определения высот точек, отметки кото­рых не подписаны на карте, равна: для характерных точек рельефа, расположенных на вершинах, гребнях, водосливах, бровках и пологих скатах неровностей, – примерно 0,3 – 0,5 высоты сечения, а для точек, расположенных на крутых скатах, где невозможно проведение полугоризонталей, она примерно в 3-4 раза меньше.

Определение формы и крутизны скатов

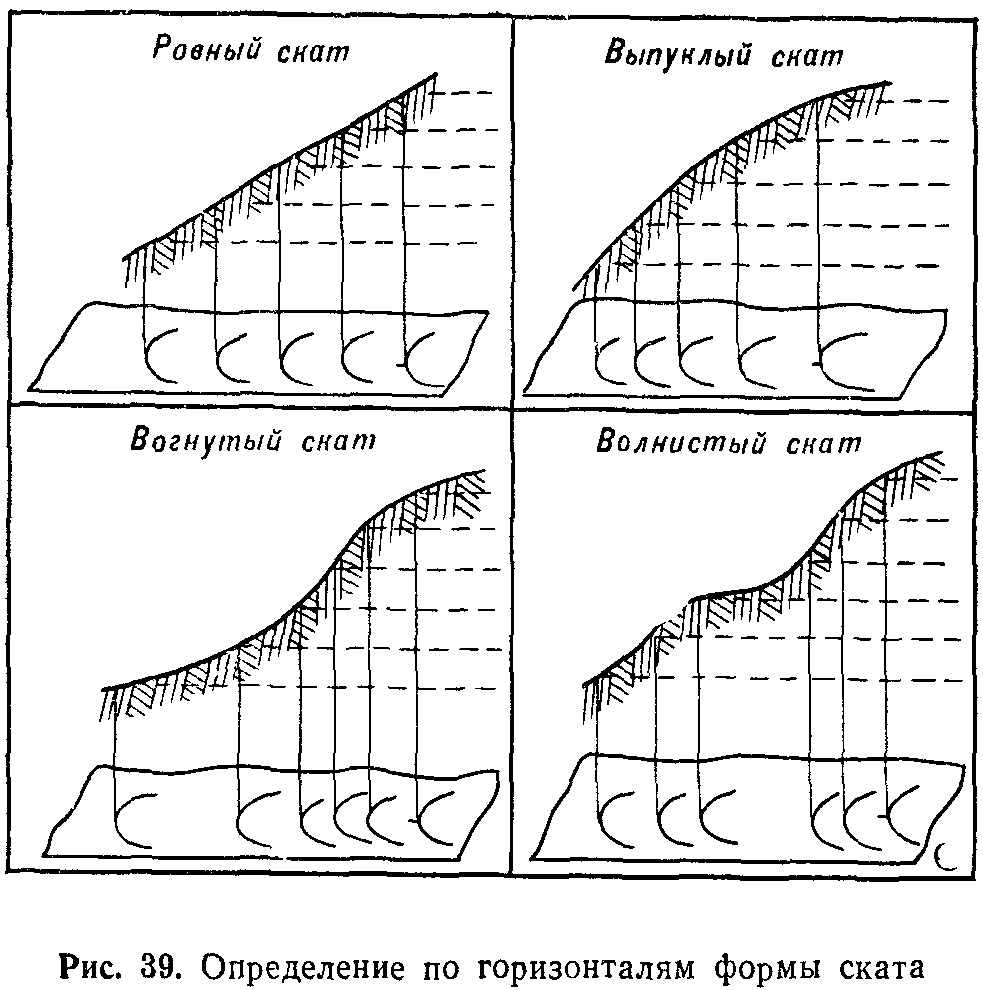
Форма ската определяется по взаимному расположению гори­зонталей на скате (рис. 39). Если скат ровный, то его гори­зонтали на карте располагаются на равных расстояниях одна от другой; при вогнутом скате они учащаются к вершине, а при выпуклом, наоборот, – к подошве. При волнистом скате горизонтали учащаются и разреживаются в нескольких местах в зависимости от количества перегибов ската.

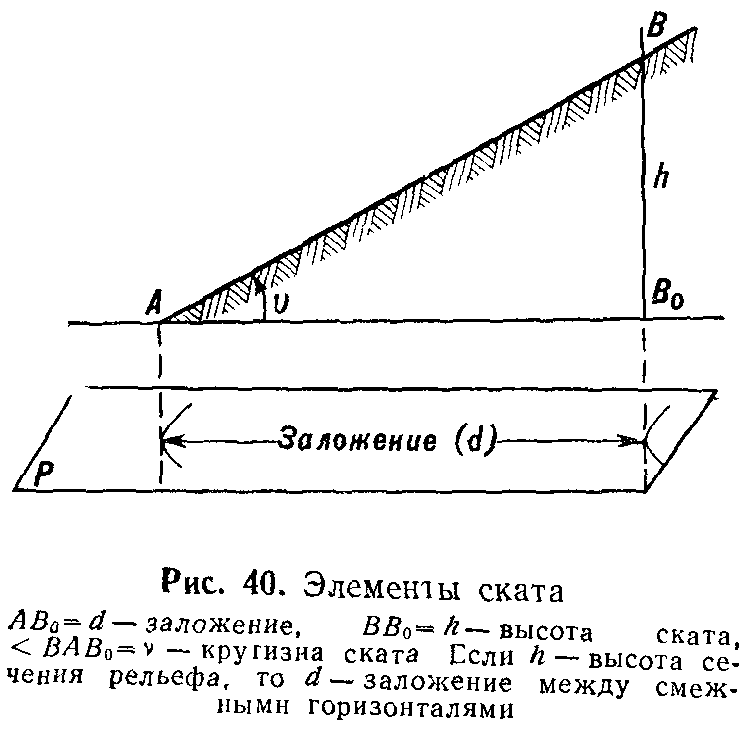
Крутизна ската, т. е. угол его наклона v (рис. 40), вы­числяется по формуле

(1)

Приближенно угол v, если он не больше 25°, может быть под­считан по формуле

(2)

Эти зависимости и лежат в основе всех способов определения крутизны скатов. Наиболее употребительны из них следующие.

А Определение крутизны скатов по шкале заложений (рис 41) шкалой заложений называется график, который печатается на всех листах топографических карт масштаба 1 : 100 000 и круп нее – рядом с линейным масштабом. Вдоль основания графика подписана крутизна скатов в градусах. На перпендикулярах к основанию отложены в масштабе карты соответствующие им заложения: в левой части шкалы – заложения при основной высоте се­чения, а в правой – при пятикратной, т. е. заложения между двумя смежными утолщенными горизонталями.

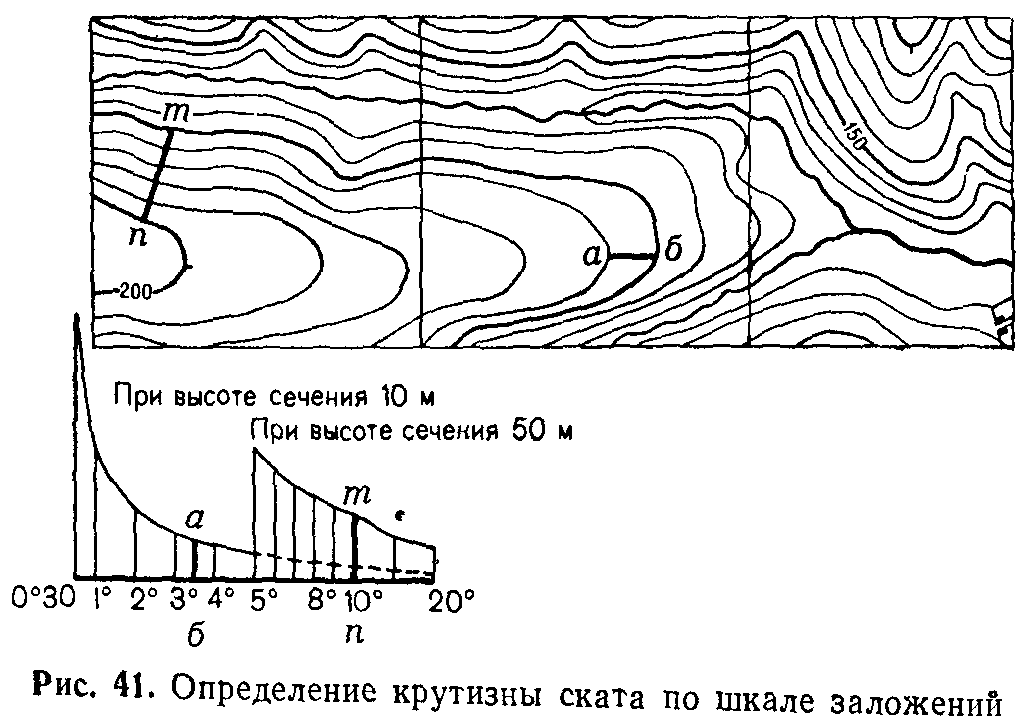
Для определения крутизны ската надо взять циркулем или с помощью полоски бумаги расстояние между двумя смежными го­ризонталями на интересующем нас скате и затем, приложив этот отрезок к шкале, как показано на рис. 41, прочитать внизу число градусов крутизны. В нашем примере крутизна ската вдоль отрез­ка ab равна 3°,5.

Если горизонтали на скате расположены очень близко одна к другой и взять циркулем расстояние между ними затруднительно, тогда удобнее пользоваться правой частью шкалы, беря при этом по карте заложения между соседними утолщенными горизонта­лями. В нашем примере крутизна ската по отрезку mn равна 10°.

Точность определения крутизны скатов по шкале заложений равна примерно 0,3-0,4 цены деления этой шкалы в том ее ин­тервале, в котором определяется крутизна данного ската.

Б. Оценка крутизны скатов на глаз. Расчеты по формуле (2) показывают, что на всех топографических картах с нормальной высотой основного сечения (т. е. при Л = 0,02 величины масштаба карты) заложению в 1 см соответствует крутизна ската в 1°,2 или округленно в 1°, а заложению в 1 мм соответствует крутизна ската в 10°. Поэтому на указанных картах применимо следующее общее правило для приближенного определения крутизны ската на глаз: определяемая крутизна ската во столько раз больше (меньше) 1°, во сколько раз его заложение между смежными сплошными гори­зонталями меньше (больше) 1 см.

Например, на карте масштаба 500 м в 1 см с высотой сечения 10 м крутизна ската будет примерно равна: при заложении ската 0,5 см – 2°, при заложении 0,1 см– 10°, при заложении 2 см – 0°,5.

Это правило применимо и на картах, на которых высота сече­ния отличается от нормальной. При этом, однако, надо получен­ное по указанному правилу число градусов увеличить (умень­шить) во столько же раз, во сколько высота основного сечения на карте больше (меньше) нормальной. Если она больше нормаль­ной, то для уточнения надо в полученный при этом результат ввести поправку, прибавив по 1° на каждые 4°.

Например, на карте масштаба 1:25 000 с высотой основного сечения 10 м (нормальная высота сечения 5 м) заложению в 0,5 см соответствует 5° (4+1), а заложению в 1 мм – 25° (20 + 5).

16