Точность измерения расстояний по карте

Опытным путем установлено, что с помощью циркуля измере­ния прямолинейных отрезков на карте и других чертежах не могут быть выполнены точнее, чем 0,2 мм. Расстояние на мест­ности, соответствующее 0,2 мм на карте, называют предельной точностью масштаба карты.

Однако точность определения расстояний по карте зависит не только от точности измерений, но и от погрешностей самой карты, неизбежных при ее составлении и печатании, которые могут дости­гать 0,5 мм, а на картах горных районов – 0,75 мм. Источниками ошибок измерений являются также помятость и деформация бу­маги. С учетом этого фактическая точность измерения прямых линий по карте, как показывает практика, колеблется в преде­лах 0,5 – 1,0 мм, что в масштабе 1:25000 на местности состав­ляет 12 – 25 м, в масштабе 1:50 000 – 25-50 м, 1:100000 – 50-100 м.

Учебный вопрос №2 «Сущность изображения рельефа на картах горизонталями».

На топографических картах рельеф изображается горизон­талями, т. е. кривыми замкнутыми линиями, каждая из которых представляет собой изображение на карте горизонтального кон­тура неровности, все точки которого на местности расположены на одной и той же высоте над уровнем моря.

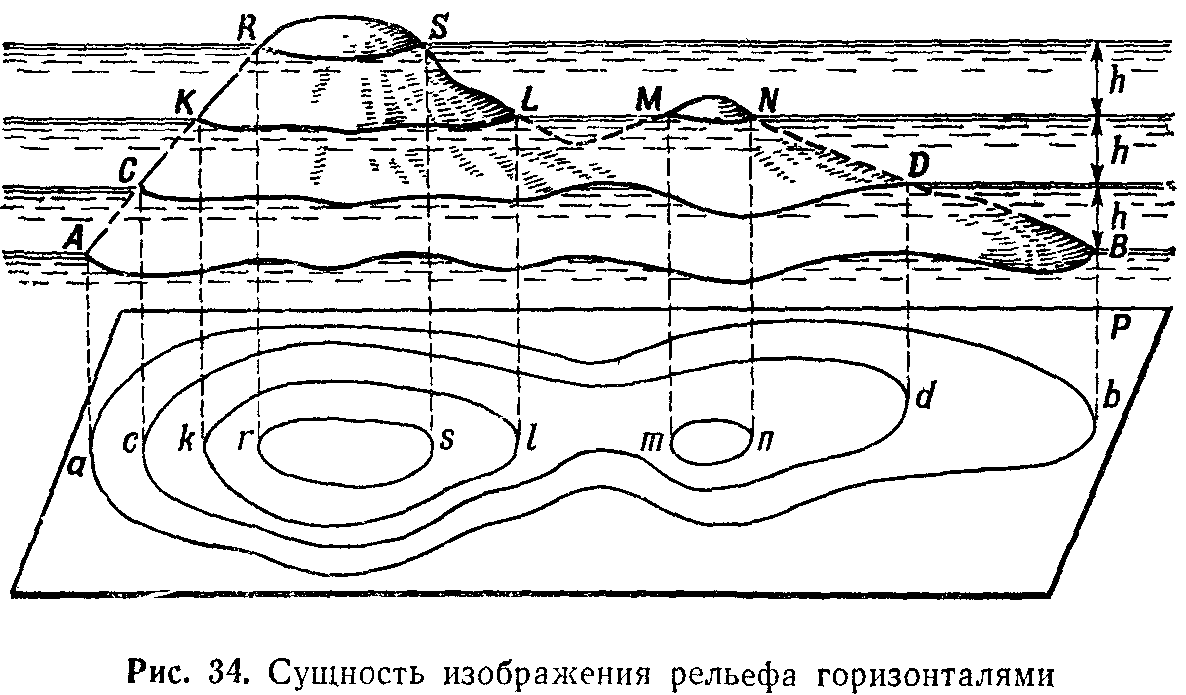
Чтобы лучше уяснить сущность изображения рельефа гори­зонталями, представим себе остров в виде горы, постепенно за­топляемой водой. Допустим при этом, что уровень воды последо­вательно останавливается через одинаковые промежутки по вы­соте, равные h метров (рис. 34).

Каждому уровню воды, начиная с исходного (линия АВ), бу­дет, очевидно, соответствовать своя береговая линия {CD, KL, MN, RS) в виде замкнутой кривой, все точки которой имеют одну и ту же высоту.

Эти линии можно рассматривать и как следы сечения неров­ностей местности уровенными поверхностями, параллельными уровенной поверхности моря, от которой ведется счет высот. Ис­ходя из этого расстояние h по высоте между смежными секущими поверхностями называется высотой сечения.

Если все эти линии равных высот спроектировать на поверх­ность земного эллипсоида и изобразить в заданном масштабе на карте, то получим на ней изображение горы в плане в виде си­стемы замкнутых кривых линий ab, cd, М, тп и rs. Это и будут горизонтали.

Из рассмотрения сущности горизонталей можно сделать сле­дующее заключение:

а) каждая горизонталь на карте представляет собой горизон­тальную проекцию линии равных высот на местности, изображаю­щую плановое очертание неровностей земной поверхности. Таким образом, по рисунку и взаимному положению горизонталей можно воспринимать формы, взаимное положение и взаимосвязь неров­ностей;

б) так как горизонтали на карте проводятся через равные про­межутки по высоте, то по числу горизонталей на скатах можно определять высоту скатов и взаимные превышения точек земной поверхности: чем больше горизонталей на скате, тем он выше;

в) заложения горизонталей, т. е. расстояния в плане между смежными горизонталями, зависят от крутизны ската: чем скат круче, тем меньше заложение. Следовательно, по величине зало­жения можно судить о крутизне ската.