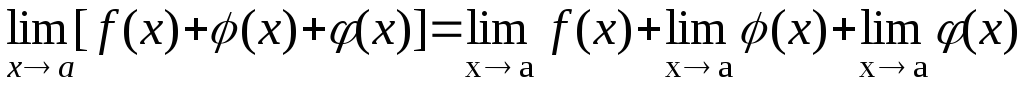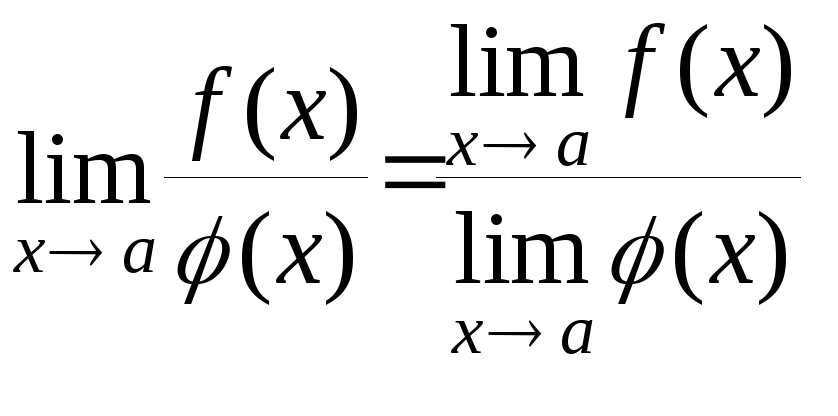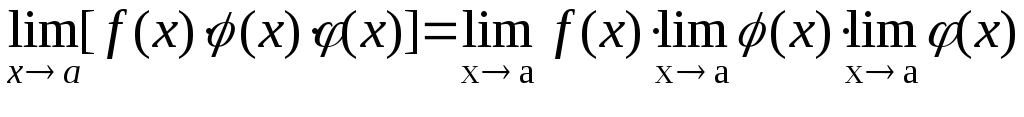Вопросы и ответы (мат)
.doc|
|
ВОПРОС |
|
|
ОТВЕТ |
|
1 |
Функция y = f(x) имеет пределом |
|
1 |
Функция y = f(x) имеет пределом число А при стремлении х к а, если для каждого числа е>0 найдется такое число δ>0, что |y — A|<е, при | х —a|<δ
|
|
2 |
Математическая запись предела |
|
2 |
|
|
3 |
Предел постоянной величины |
|
3 |
limА=А
|
|
4 |
Предел суммы (разности) конечного числа функций |
|
4 |
|
|
5 |
Предел частного двух функций |
|
5 |
|
|
6 |
Предел произведений конечного числа функций
|
|
6 |
при lim φ(x)≠0
|
|
7 |
Чему равен замечательный предел:
|
|
7 |
|
|
8 |
Чему равен замечательный предел:
|
|
8 |
|
Производная. Применение производных для исследования функций
|
|
ВОПРОС |
|
|
ОТВЕТ |
|
1 |
Производной функции f(x) называется |
|
1 |
Производной функции f(x) называется предел отношения приращения функции Δу к приращению аргумента Δх в точке х при стремлении Δх к нулю: |
|
2 |
Математическая запись производной |
|
2 |
|
|
3 |
Производная постоянной величины у=С: |
|
3 |
ý= 0; |
|
4 |
Производная степенной функции у = хμ: |
|
4 |
ý=μxμ-1 |
|
5 |
Производная показательной функции у = аx: в частности, если у = ех |
|
5 |
ý=axlna; ý= еx; |
|
6 |
Производная логарифмической функции y=logax
|
|
6 |
|
|
7 |
Производная натурального логарифма у = lnх |
|
7 |
|
|
8 |
Производная тригонометрической функции y=sinx |
|
8 |
y'=cosx; |
|
9 |
Производная тригонометрической функции y=cos x |
|
9 |
ý =— sin x; |
|
10 |
Производная тригонометрической функции y = tgx |
|
10 |
|
|
11 |
Производная тригонометрической функции y = ctgx |
|
11 |
|
|
12 |
Производная обратной тригонометрии-ческой функции y=arcsinx
|
|
12 |
|
|
13 |
Производная обратной тригонометрии-ческой функции y=arccosx |
|
13 |
|
|
14 |
Производная обратной тригонометрии-ческой функции y=arctgx
|
|
14 |
|
|
15 |
Производная обратной тригонометрии-ческой функции y=arcctgx |
|
15 |
|
|
16 |
Производная суммы (разности) функций y = w±u |
|
|
y' = u'±v' |
|
17 |
Производная произведения двух функций y=uv |
|
17 |
y' = u'v + v'u. |
|
18 |
Производная частного двух функций y=u/v |
|
18 |
|
|
19 |
Производная сложной функции y = f1(u), если u = f2(x), |
|
19 |
у'x = у'ии'x |
|
20 |
Условие возрастания функции y = f(x) на отрезке [а, b] |
|
20 |
f'(x)>0
|
|
21 |
Условие убывания функции y=f(x) на отрезке [а, b]
|
|
21 |
f'(x)<0
|
|
22 |
Условие максимума функции y=f(x) при x= а
|
|
22 |
f'(a)=0 и f'' (a)<0
|
|
23 |
Условия функции экстремума |
|
|
Если при х=а производные f'(а) = 0 и f"(а) = 0, то необходимо исследовать f'(x) в окрестностях точки x = а. Функция у=f(х) при х=а имеет максимум, если при переходе через точку х= а производная f'(x) меняет знак с «+» на «-», в случае минимума — с « - » на «+» Если f'(x) не меняет знака при переходе через точку х = а, то в этой точке у функции экстремума нет |
Дифференциал функции. Применение
дифференциала в приближенных вычислениях
|
|
ВОПРОС |
|
|
ОТВЕТ |
|
1 |
Дифференциал независимой переменной равен |
|
1 |
ее приращению: dx=Δx |
|
2 |
Дифференциал функции y=f(x) |
|
2 |
dy = у' Δх |
|
3 |
Дифференциал суммы (разности) двух функций y=u±v
|
|
3 |
dy=du±dv |
|
4 |
Дифференциал произведения двух функций у=uv
|
|
4 |
dy = vdu+udv.
|
|
5 |
Дифференциал частного двух функций y=u/v |
|
5 |
|
|
6 |
Приращение функции через дифференциал |
|
6 |
Δy = f(x + Δx) - f(x) ≈ dy ≈ f'(x) • Δx где Δx: — приращение аргумента |
|
7 |
Приближенное вычисление значения функции:
|
|
7 |
f(x + Δx) ≈ f(x) + f'(x) • Δx
|
|
8 |
Дифференциал применяется для вычисления абсолютной и относительной погрешностей при косвенных измерениях u = f(x, у, z .). Абсолютная погрешность результата измерения
|
|
8 |
|
|
9 |
Относительная погрешность результата измерения
|
|
9 |
|
![]()
Неопределенный интеграл
|
|
ВОПРОС |
|
|
ОТВЕТ |
|
1 |
первообразной данной функции f(x) называется |
|
1 |
Функция F(x), имеющая данную функцию f(x) своей производной или f(x)dx своим дифференциалом, называется первообразной данной функции f(x). |
|
2 |
неопределенным интегралом называется |
|
2 |
Совокупность всех первообразных функций для дифференциала f(x)dx называется неопределенным интегралом и обозначается символом ∫ f(x)dx. |
|
3 |
Интеграл ∫xμdx равен |
|
3 |
xμ+1/ (μ+1) +C (μ≠-1) |
|
4 |
Интеграл ∫dx/x равен |
|
4 |
ln|x|+C |
|
5 |
Интеграл ∫axdx равен |
|
5 |
ax/lna +C |
|
6 |
Интеграл ∫exdx равен |
|
6 |
ex+C |
|
7 |
Интеграл ∫sin x dx равен |
|
7 |
-cos x +C
|
|
8 |
Интеграл ∫cos xdx равен |
|
8 |
sin x +C |
|
9 |
Интеграл ∫dx/cos2x равен |
|
9 |
tgx+C |
|
10 |
Интеграл ∫dx/sin2x равен |
|
10 |
-ctgx+C
|
|
11 |
Интеграл ∫dx равен |
|
11 |
х+С |
|
12 |
Интеграл ∫arc sinxdx равен |
|
12 |
|
|
13 |
Интеграл ∫arc cosxdx равен |
|
13 |
- |
|
14 |
Интеграл ∫arc tgxdx равен |
|
14 |
|
|
15 |
Интеграл ∫arc ctgxdx равен |
|
15 |
- |
|
16 |
Интеграл ∫tgxdx равен |
|
16 |
Lncosx+C |
|
17 |
Интеграл ∫ctgxdx равен |
|
17 |
- Lnsinx+C |
|
18 |
Интегрирование по частям
|
|
18 |
∫ udv = uv—∫ vdu.
|
|
19 |
Найти у = ∫ In хdх. |
|
19 |
Полагаем
и=lпх,
dv
= dx,
тогда
Используя формулу интегрирования по частям, получаем
у = ∫ In xdx = x In х-∫ dх = xlnx-x+C
|
|
20 |
Интегрирование методом замены переменных Найти у= ∫ (1+ 2x2)dx |
|
20 |
Заменим l+2x=z,
y=0,5∫z2dz
Возвращаясь к прежней переменной х, окончательно имеем
|