
- •Сравнение групп
- •Нулевая гипотеза
- •Две оценки дисперсии
- •Критическое значение f
- •Критерий стьюдента
- •Принцип метода
- •Критерий Стьюдента для множественных сравнений
- •Анализ качественных признаков
- •Точность оценки долей
- •Сравнение долей
- •Поправка Йейтса на непрерывность
- •Тромбоз шунта у больных на гемодиализе
- •Критерии χ2 для таблицы 2×2
- •Точный критерий Фишера
- •Непараметрическое множественное сравнение.
Сравнение групп
Часто возникает задача сравнить группы между собой. Такая задача может возникнуть, если необходимо выявить какой метод лечения более эффективный или имеется ли значимое отличие между действием какого-то препарата и плацебо в ходе проверки эффективности вводимого лекарства и т.д. Часто в подобных исследованиях одна из групп испытуемых принимается за контрольную – например, группа, которую лечили эталонным методом лечения или давали препарат плацебо вместо испытуемого лекарства, другая группа – экспериментальная. Сравнив между собой исследуемые показатели, исследователь делает вывод согласно цели эксперимента.
2
Нулевая гипотеза
Результатом исследования обычно является утверждение, имеющее жизненно важное значение, например, какой самый лучший метод лечения рака, каковы самые распространенные побочные эффекты определенного вида хирургического вмешательства, каков коэффициент выживаемости после определенного лечения и действительно ли новое экспериментальное лекарство увеличивает продолжительность жизни.
Однако, прежде чем получить результат (утверждение), необходимо правильно планировать ход исследования, одним из важных этапов является формулировка исходного утверждения, правильность которого и проверяется в ходе исследования. Такое утверждение называется гипотезой.
Гипо́теза (др.-греч. ὑπόθεσις — предположение; от ὑπό — снизу, под + θέσις — тезис) —утверждение, предполагающее доказательство.
Проверка гипотезы — это статистическая процедура, предназначенная для проверки утверждения. Обычно утверждение касается параметра совокупности (т.е. одного числа, характеризующего всю совокупность). Поскольку параметры чаще всего неизвестны, то все хотят высказаться о том, какими могут быть эти значения. К примеру, утверждение о том, что 25% всех женщин старше определенного возраста страдают варикозным расширением вен — это утверждение о доле (это и есть параметр) всех женщин (т.е. генеральной совокупности), у которых наблюдается варикозное расширение вен (это переменная, потому что варикозное расширение вен может быть, а может и нет). Или среднее время госпитализации у первой исследуемой группы составило 4,5 суток, у второй – 6,3 суток (переменная – время госпитализации, параметр – среднее значение дней госпитализации).
После того как исследователь определил переменную и параметр, влияние на которую того или иного фактора проверяется в исследовании, он формулирует нулевую гипотезу.
Нулевая гипотеза - это предположение, что исследуемые факторы не оказывают никакого влияния на исследуемую величину и полученные различия (исследуемых параметров) случайны. Например, сравнивая различающиеся средние значения артериального давления при применении двух разных анестетиков, мы выдвигаем нулевую гипотезу о том, что полученные различия не значительны.
Альтернативная гипотеза обратна нулевой гипотезе. В исследовании обычно формулируется именно нулевая гипотеза, т.е., то, что мы хотим опровергнуть.
3
СТАТИСТИЧЕСКАЯ ЗНАЧИМОСТЬ РЕЗУЛЬТАТОВ.
УРОВЕНЬ ЗНАЧИМОСТИ
Получив результат, исследователь делает вывод о том, значим ли полученный результат с точки зрения статистического анализа. Другими словами он делает вывод о статистической значимости полученного результата.
Для того, чтобы сделать вывод о наличии или отсутствии статистической значимости используется так называемый критерий значимости. Полученное числовое значение критерия значимости указывает на то, принимается или отвергается нулевая гипотеза. Однако, вывод зависит и от того с какой вероятностью мы можем получить наблюдаемые результаты при верности нулевой гипотезы. Другими словами, мы допускаем наличие ошибки, и максимальную вероятность ее возникновения устанавливаем сами. Если эта вероятность мала, то мы отвергаем нулевую гипотезу и заключаем что результаты эксперимента статистически значимы. Максимальную приемлемую вероятность отвергнуть верную нулевую гипотезу называют уровнем значимости и обозначают α. Обычно принимают α = 0,05 (5%). Это, разумеется, еще не означает что мы доказали действие именно изучаемых факторов (это вопрос прежде всего планирования эксперимента), но, во всяком случае, маловероятно, что результат обусловлен случайностью.
Если в ходе исследования мы получили результат, который отвергает нулевую гипотезу, при уровне значимости 5%, то можно сказать следующее: если бы нулевая гипотеза была справедлива, то вероятность получить наблюдаемые результаты была бы меньше 5%. В принятой системе обозначений это записывается как Р < 0,05. Р есть вероятность ошибочно отвергнуть нулевую гипотезу.
Отсюда мы заключаем, что гипотеза об отсутствии влияния препарата, например, на давление, вряд ли справедлива, то есть различия статистически значимы (при 5% уровне значимости). Разумеется, этот вывод по сути своей носит вероятностный характер. Не исключено, что мы ошибочно признаем неэффективный препарат эффективным, то есть найдем различия там, где их нет. Однако мы можем утверждать, что вероятность подобной ошибки не превышает 5%.
4
ОШИБКИ ПЕРВОГО И ВТОРОГО РОДА.
Исходя из последнего утверждения, различают ошибки первого и второго рода.
Если мы ошибочно отклоняем нулевую гипотезу, например, находим различия там, где их нет, то это называется ошибкой I рода.
Максимальная приемлемая вероятность ошибки I рода и есть уровень значимости. Обычно α принимают равной 0,05 (то есть 5%), однако можно взять и какой-нибудь ругой уровень значимости, например 0,1 или 0,01.
Если мы не отклоняем нулевую гипотезу, когда она не верна, то есть не находим различий там, где они есть, то это — ошибка II рода.
5
МЕТОДЫ АНАЛИЗА РАЗЛИЧИЙ
ДИСПЕРСИОННЫЙ АНАЛИЗ
Проведем гипотетический эксперимент. Однажды в небольшом городке (200 жителей) ученые исследовали влияние диеты на сердечный выброс. Случайным образом отобрали 28 человек, каждый из которых согласился участвовать в исследовании. После этого они опять таки случайным образом были разделены на 4 группы по 7 человеке каждой.
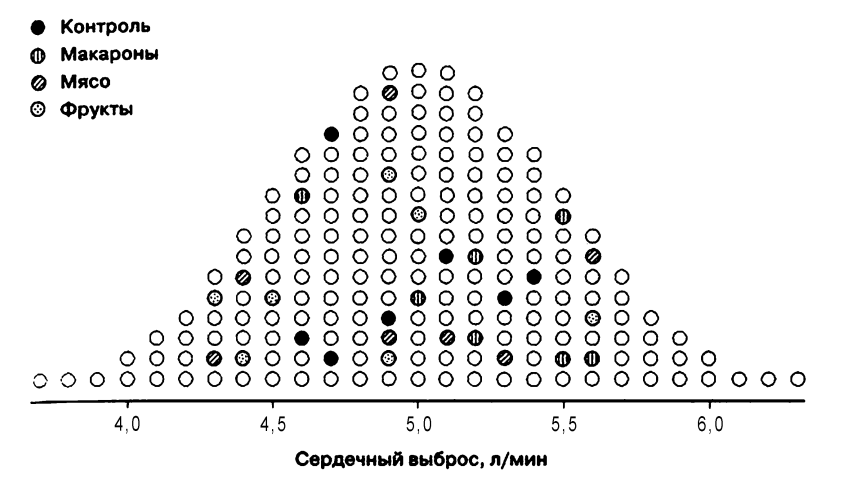
Члены первой (контрольной) группы продолжали питаться как обычно, члены второй группы стали есть только макароны, третьей группы — мясо, четвертой — фрукты. Члены наших экспериментальных групп изображены заштрихованными кружками. Через месяц у всех участников эксперимента измерили сердечный выброс.
Анализ данных мы начинаем с формулировки нулевой гипотезы. В данном случае она заключается в том, что ни одна из диет НЕ влияет на сердечный выброс
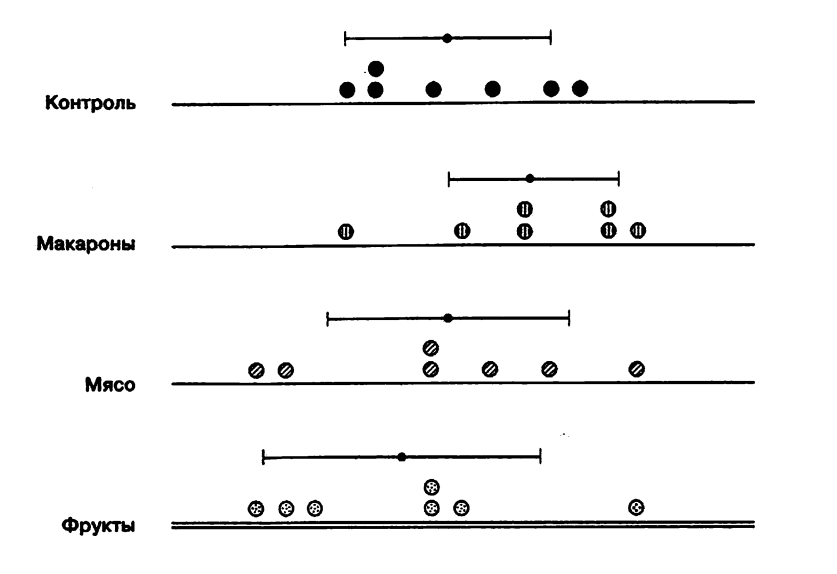
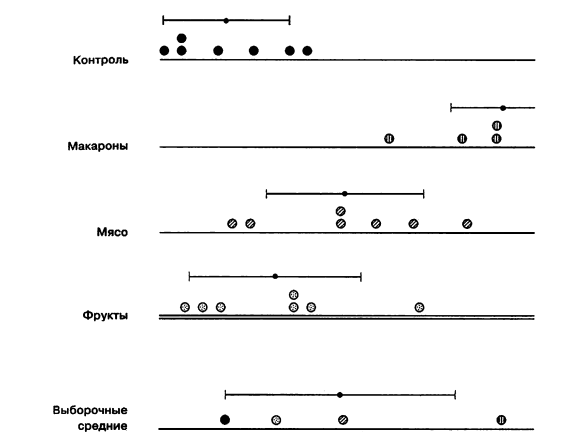
Как видно из рисунка, группы все же различаются по средней величине сердечного выброса. Вопрос можно поставить так: какова вероятность получить такие различия, извлекая случайные выборки из нормально распределенной совокупности? Прежде чем ответить на этот вопрос нам надо получить показатель, характеризующий величину различий.
6

7
Чтобы оценить величину различий, нужно каким-то образом сравнить разброс выборочных средних с разбросом значений внутри групп.
Сейчас мы покажем, как это можно сделать с помощью дисперсии (как мы выяснили, этот показатель характеризует именно разброс), но прежде сделаем несколько замечаний.
Дисперсия правильно характеризует разброс только в том случае, если совокупность имеет нормальное распределение. Поэтому и критерий, основанный на дисперсии, применим только для нормально распределенных совокупностей. Вообще, все критерии, основанные на оценке параметров распределения (они называются параметрическими), применимы только в случае, если данные подчиняются соответствующему распределению (чаще всего речь идет о нормальном распределении). Если распределение отличается от нормального, следует пользоваться так называемыми непараметрическими критериями. Эти критерии не основаны на оценке параметров распределения и вообще не требуют, чтобы данные подчинялись какому-то определенному типу распределения. Непараметрические критерии дают более грубые оценки, чем параметрические. Параметрические методы более точны, но лишь в случае, если правильно определено распределение совокупности.
8
