
- •Лекция 4
- •НУЛЕВАЯ ГИПОТЕЗА
- •СТАТИСТИЧЕСКАЯ ЗНАЧИМОСТЬ
- •ОШИБКИ ПЕРВОГО И ВТОРОГО РОДА
- •МЕТОДЫ АНАЛИЗА РАЗ
- •Возможные варианты различий средних между группами
- •Чтобы оценить величину различий, нужно каким-то
- •Дисперсию совокупности можно оценить двумя
- •Если верна нулевая гипотеза, то как внутригрупповая, так и межгрупповая дисперсии служат оценками
- •Критическое значение F
- •Межгрупповое число степеней свободы —
- •Дисперсионный анализ, в котором проверяется влияние одного фактора, называется однофакторным. При изучении
- •Итак, на наш вопрос можно ли считать различия в длительности госпитализации случайными мы
- •КРИТЕРИЙ СТЬЮДЕНТА
- •Для двух случайных выборок извлеченных из одной
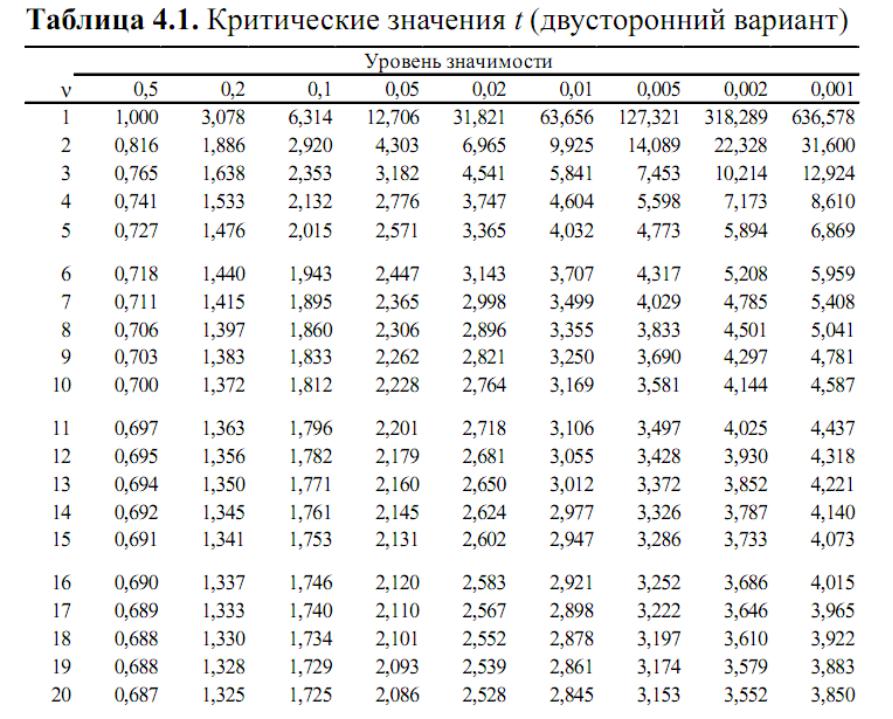
- •Критические значения t (подобно критическим значениям F они сведены в таблицу) зависят не
- •Ошибки в использовании критерия Стьюдента
- •АНАЛИЗ КАЧЕСТВЕННЫХ ПРИЗНАКОВ
- •СРАВНЕНИЕ ДОЛЕЙ
- •Таблицы сопряженности: кр
- •Критерии χ2
- •Критическое значение χ2 для 5% уровня
- •Точный критерий Фишера
- •НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ
- •Параметрические и непараметрические
- •Непараметрические
- •ВЫВОДЫ
Межгрупповое число степеней свободы —
это число групп минус единица νмеж = m – 1.
Внутригрупповое число степеней свободы
— это произведение числа групп на численность каждой из групп минус единица νвну = m (n – 1).

Дисперсионный анализ, в котором проверяется влияние одного фактора, называется однофакторным. При изучении
влияния более чем одного фактора используют многофакторный
дисперсионный анализ.
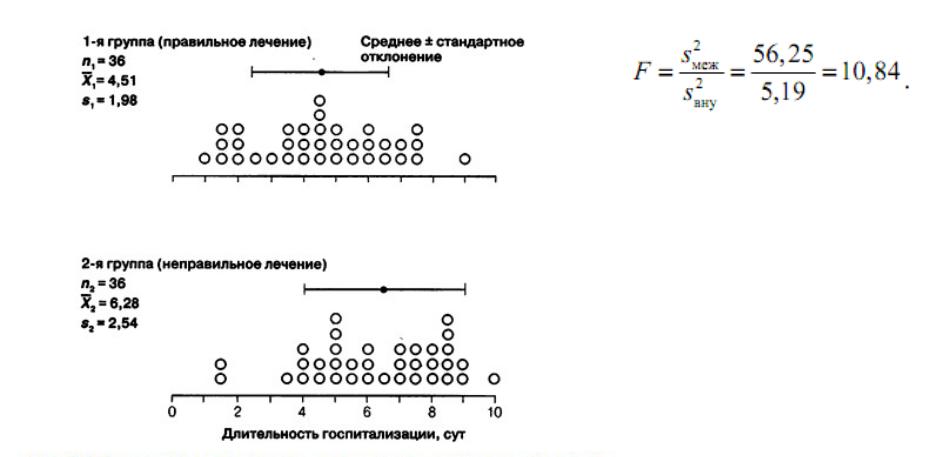
Итак, на наш вопрос можно ли считать различия в длительности госпитализации случайными мы можем дать ответ,
вероятность этого весьма мала меньше 1%. Леченные правильно находились в больнице меньше чем, леченные
неправильно и различия эти
Рассчитаем межгрупповое и внутри групповое число степеней свободы νмеж = 2 –
1 = 1, νвну = 2 (36 –
1) = 70. Теперь по таблице 3.1 найдем критическое значение F. На
пересечении столбца «1» и строки «70» находим число 7,01,
набранное жирным
шрифтом. То есть
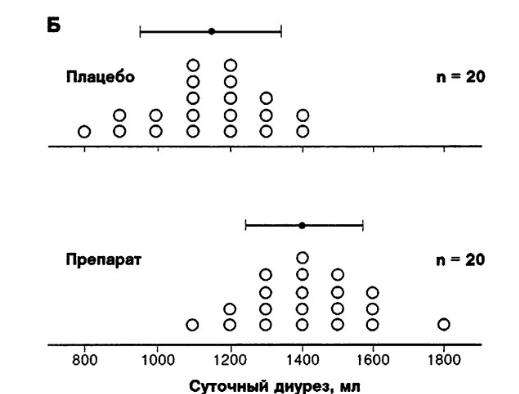
КРИТЕРИЙ СТЬЮДЕНТА
Критерий Стьюдента чрезвычайно популярен, он используется более чем в половине медицинских публикаций. Однако следует помнить, что этот
критерий предназначен для сравнения именно двух групп, а не нескольких групп попарно.
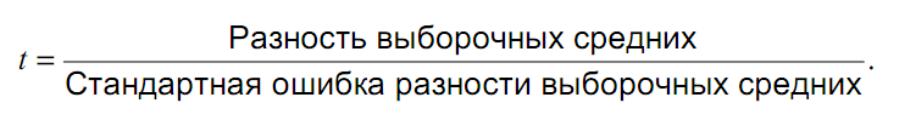
Для двух случайных выборок извлеченных из одной
нормально распределенной совокупности это
отношение, как правило, будет близко к нулю.
Чем меньше (по абсолютной величине) t, тем больше вероятность нулевой гипотезы. Чем больше t, тем больше оснований отвергнуть нулевую гипотезу и считать, что различия
статистически значимы.
Если значение t меньше –2,1 или больше +2,1, то при уровне значимости 0,05 мы сочтем различия статистически значимыми. Это означает,
что если бы наши группы представляли собой две случайные выборки из одной и той же совокупности, то вероятность получить наблюдаемые различия (или более сильные) равна 0,05. Следовательно,
Критические значения t (подобно критическим значениям F они сведены в таблицу) зависят не только от уровня значимости, но и от числа степеней свободы ν= 2(n – 1), где n – объем выборок. Чем больше объем выборок, тем меньше критическое значение t.
Ошибки в использовании критерия Стьюдента
Критерий Стьюдента предназначен только для сравнения двух групп. Однако на практике он широко используется для оценки различии большего числа групп посредством попарного их сравнения. Что не верно. При этом вступает в силу эффект
множественных сравнений. Три правила:
•Критерий Стьюдента может быть использован для проверки гипотезы о различии средних только для двух групп.
•Если схема эксперимента предполагает большее число групп, воспользуйтесь дисперсионным анализом.
•Если критерии Стьюдента был использован для проверки различий между несколькими группами, то истинный уровень значимости можно получить, умножив уровень значимости, приводимый авторами
на число возможных сравнений.
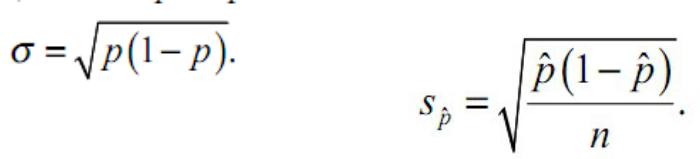
АНАЛИЗ КАЧЕСТВЕННЫХ ПРИЗНАКОВ
Единственный способ описания качественных
признаков состоит в том, чтобы подсчитать число объектов, имеющих одно и то же значение. Кроме
того, можно подсчитать, какая доля от общего
числа объектов приходится на то или иное
Для характеристики. совокупности, которая состоит из
значение двух классов, достаточно указать численность одного
из них если доля одного класса во всей совокупности равна р (вероятность), то доля другого равна 1 – р.
