Лабораторная работа №1. Основные термины. Знакомство с программами для статистического анализа: пакет анализа MS Excel и Statistica 6.

Основы статистики

ЛАБОРАТОРНАЯ РАБОТА №1. ОСНОВНЫЕ ТЕРМИНЫ. ЗНАКОМСТВО С ПРОГРАММАМИ ДЛЯ СТАТИСТИЧЕСКОГО АНАЛИЗА: ПАКЕТ АНАЛИЗА MS EXCEL И STATISTICA 6.

Жученко Ю.М., Ковалев А.А., Игнатенко В.А.

Лабораторная работа №1 Основные термины. Знакомство с программами для статистического анализа: пакет анализа ms Excel и Statistica 6. Краткие сведения из теории

Биомедицинская информация - это сведения о свойствах биологических объектов и явлениях, являющихся предметами медицинских исследований, а также представления и суждения об этих свойствах и явлениях.

Биомедицинская статистика– инструмент для анализа данных, полученных в ходе эксперимента и клинических наблюдений из повседневной практики, а также язык, с помощью которого исследователь сообщает читателю полученные им результаты.

Какие бывают данные?

Любое статистическое исследование в первую очередь работает с данными (показателями или признаками того или иного исследуемого объекта).

Данные полученные в ходе эксперимента могут быть качественными, количественными ипорядковыми.Для корректного использования статистических методовважнопредставлять, какого типа данные будут обрабатываться.

Количественные данные- признаки, которые можно выразить в числовой форме: возраст, вес, количество детей в семье и т.п.. В свою очередь, они делятся нанепрерывныеидискретные.

Непрерывные данные(continuous data) - количественные данные, которые могут принимать любое значение на непрерывной шкале. Другое название –признаки, измеряемые в интервальной шкале(температура, артериальное давление, рост) Например, рост взрослого человека может приниматьлюбоезначение в интервале от 150 см до 220 см: 178 см, 178,25 см, 182,33456 см, т.е. произвольное числовое значение на шкале в заданном интервале.

Дискретные данные (discrete data) - количественные данные, принимающие, как правило, конечное число значений, хотя иногда и очень большое: количество смертей в течение года в исследуемой группе, количество пропущенных по болезни рабочих дней.

Качественные данные(классификационные, неупорядоченные, номинальные) - это признаки, которые нельзя выразить количественно: диагноз, место проживания, пол, жив человек или мертв, есть температура или нет и т.п.

Порядковые данные- показатели, измеряемые в шкале порядка (например, стадии болезни, оценки – «плохо», «удовлетворительно», «хорошо»). При этом порядок изменить нельзя, только в обратном направлении, но смысл от этого не меняется. Такие признаки могут быть осмысленно оцифрованы, но важно понимать, что порядок состояний имеет смысл. Часто к таким показателям следует относить балльные оценки, полученные при проведении тестов или экспертиз. Особенность порядковых шкал – отсутствие количественного измерения расстояний между величинами на шкале (можно сказать, что течение болезни «хуже», чем среднетяжелое, при этом очень тяжелое «еще хуже», однако сложно сказатьво сколько раз«хуже»)

Для различных типов переменных применяются разные методы статистического анализа

Генеральная совокупность и выборка. Свойства выборки

Обычно исследователь в ходе статистического анализа стремиться сделать выводы обо всей совокупности объектов (например, как некий препарат воздействует на каждого человека с конкретной болезнью). В сущности, в этом и заключается смысл анализа: иметь представление о свойствах всехизучаемых объектов по тому или иному признаку (например, артериальное давление –признак, люди в возрасте от 30 до 45 лет –исследуемый объект). Весь массив исследуемых объектов образуетгенеральную совокупность. Генеральная совокупность обычно представляет собой достаточнобольшое число элементов, исследователь, в силу различных факторов не может осуществить эксперимент над всеми элементами генеральной совокупности, поэтому он останавливается на достаточном количестве элементов, по возможностихарактеризующим всю генеральную совокупность. Это количество исследуемых объектов называютсявыборкой. Предполагается, что выборкахарактеризует всю генеральную совокупность, если это условие выполняется, то такую выборку называютрепрезентативной (представительной).Репрезентативность– очень важное свойство выборки, если выборка не является репрезентативной, то исследователь может сделать ошибочные выводы обо всех объектах исследования (всей генеральной совокупности) Стоит заметить, что в медицинских исследованиях часто бывает так, что выборки имеют очень небольшой объем (обычно в формулах число элементов выборки обозначается какn), порядка 10-20 элементов.

Обеспечение репрезентативности выборки важныйаспект при планировании статистического исследования. При недостаточно качественном выполнении данного условия имеется большой шанс получить превратные представления об исследуемом объекте

Классический пример

Классический пример нерепрезентативной выборки, произошедший в 1936 году в США во время президентских выборов.

Журнал «Литэрари дайджест», который до этого весьма успешно прогнозировал результаты предыдущих выборов, на этот раз ошибся в своих прогнозах, хотя разослал несколько миллионов письменных вопросов подписчикам, а также респондентам, которых они выбрали из телефонных книг и из списков регистрации автомобилей. В 1/4 бюллетеней, которые вернулись заполненные обратно, голоса распределились следующим образом: 57 % отдали первенство кандидату от республиканцев по имени Альф Лэндон, а 41 % отдали предпочтение действующему президенту - демократу Франклину Рузвельту.

В действительности, на выборах победил Ф. Рузвельт, который набрал почти 60 % голосов. Ошибка «Литэрари дайджест» была в следующем. Они захотели увеличить репрезентативность выборки. А так как они знали, что большинство их подписчиков относят себя к республиканцам, то они решили расширить выборку за счёт респондентов, выбранных ими из телефонных книг и автомобильных регистрационных списков. Но они не учли существующих реалий и фактически отобрали ещё больше сторонников республиканцев, потому что во времена Великой депрессии иметь автомобили и телефоны мог позволить себе средний и высший класс. А это и были по большей части республиканцы, а не демократы.

Еще одним важным свойством выборки является ее случайный характер(рандомизация). Это означает, что каждый член генеральной совокупностиравновероятноможет попасть в выборку для проведения эксперимента.

Т.е. вероятность оказаться в выборке одинакова для всех членов генеральной совокупности

Осуществить рандомизацию выборки необходимо с целью снижения возможной подтасовки результатов. Например, если исследуется воздействие препарата на артериальное давление и в генеральную совокупность входят люди разной возрастной группы, но с одинаковыми показаниями к препарату, стоит учитывать, что исследователь может выбрать людей помладше, тем самым улучшить показатели воздействия препарата, и подобный отбор уже не является случайным. Следовательно, выводы могут оказаться завышенными или заниженными, слишком оптимистичными или наоборот.

Распределение значений признака. Полигон частот

Каждая генеральная совокупность характеризуется распределениемзначений исследуемой переменной (признака) или графическим представлениемчастоты встречаемости.

Другими словами, графическим представлением того как часто (сколько раз) появляется в результатах эксперимента то или иное значение переменной

Выборка также характеризуется распределением признака (выборочное распределение).

Пример:

В результате исследования группы людей на предмет влияния правильности метода лечения на сроки госпитализации (где переменной является число дней госпитализации) были получены следующие значения:

Количество дней госпитализации

2

2,5

2,5

3

3

3

3,5

3,5

3,5

4

4

4

4

4,5

4,5

4,5

4,5

4,5

5

5

5

5,5

5,5

Запишем их в виде таблицы частот:

Количество дней	Частота
2	1
2,5	2
3	3
3,5	3
4	4
4,5	5
5	3
5,5	2

Под частотойподразумеваетсясколько разто или иное значениепоявилосьв выборке в ходе проведения эксперимента или сбора данных.

Для построения графика распределения на оси Х (горизонтальной) отмечаются значения «Количество дней госпитализации», по оси У (вертикальной) – отмечаетсясколько раз то или иное значение появилось в ходе исследования.

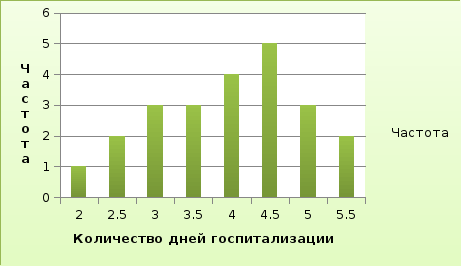
Обычно строят огибающую (линию тренда):

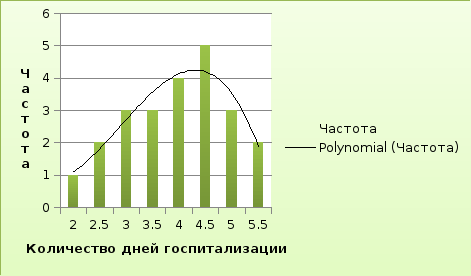
Столбчатую диаграмму чаще всего называют полигоном частот, огибающую линию –графикомраспределения частот.

Довольно часто вместо частоты встречаемостина графике изображаютотносительную частоту встречаемости.

Относительная частота встречаемостиконкретного члена выборки (или генеральной совокупности) объемомNопределяется следующим образом: