4.2. Магнитное напряжение воздушного зазора

В воздушном зазоре электрической машины индукция непосто­янна. При распределенной обмотке она изменяется по кривой, близ­кой к синусоиде (рис. 4.2, а), а при сосредоточенных обмотках имеет форму, приближающуюся к прямоугольнику (рис. 4.2, 6). Значение потока на полюсном делении

B_δx dx (4.3)

где l_δ — расчетная длина магнитопровода; В_δх — индукция в зазоре в точке х.

В практических расчетах элект­рических машин производить интег­рирование неудобно, тем более что точное аналитическое выражение распределения индукции вдоль дуги полюсного деления получить труд­но. Поэтому вводится понятие рас­четной полюсной дуги b_δ, на протя­жении которой индукция принима­ется постоянной. Значение b_δ нахо­дится из условия равенства потоков в воздушном зазоре на единицу дли­ны магнитопровода:

B_δx dx (4.4)

где В_δ — максимальное значение ин­дукции в воздушном зазоре.

Величина b_δ определяется как часть полюсного деления машины:

b_δ = α_δ τ (4.5)

где α_δ — коэффициент полюсного перекрытия; его значение, как сле­дует из определения b_δ , зависит от формы кривой поля в воздушном зазоре.

Рис. 4.2. Распределение индукции в воздушном зазоре на полюсном

де­лении электрической машины: а — с распределенной обмоткой;

б — с сосредоточенной обмоткой (с явно выра­женными полюсами)

При синусоидальном распределении индукции по длине полюс­ного деления неявнополюсных машин

α_δ = 2/π ≈ 0,64. (4.6)

При насыщении зубцов кривая поля уплощается и значение α_δ возрастает. Для средненасыщенных машин значение α_δ лежит в пре­делах 0,7 — 0,74, но при больших насыщениях может превышать 0,8.

В машинах с явно выраженными полюсами форма кривой поля зависит от конфигурации, размеров и вида полюсных наконечни­ков, поэтому расчетная длина полюсной дуги b_δ определяется в за­висимости от размерных соотношений полюсных наконечников и зазора. Методы расчета b_δ для машин с явно выраженными полюса­ми приведены в главах книги, в которых рассматривается проекти­рование машин этих типов.

Картина поля в воздушном зазоре в осевой плоскости (рис. 4.3) показывает, что индукция по длине зазора также неодинакова. Про­тив вентиляционных каналов она будет несколько меньше, чем на участках, лежащих против пакетов сердечника. Кроме того, часть магнитных линий потока замыкается через торцевые поверхности сердечника. Так как в расчетах используется постоянное значение В_δ, то для правильного определения потока через зазор вводится по­нятие расчетной длины магнитопровода l_δ, при определении кото­рой учитывается неравномерность распределения В_δ вдоль зазора. Расчетная длина может быть найдена аналитическим решением, графическим построением по картине поля или аналогично опреде­лению b_δ, т. е. из условия

B_δz dz (4.7)

определяющего равенство площадей прямоугольника длиной l_δ и вы­сотой В_δ и площади криволинейной фигуры, ограниченной действи­тельной кривой распределения индукции вдоль зазора (см. рис. 4.3).

Исследования показали, что доля потока полюсного деления, линии которого замыкаются через торцевые поверхности сердечни­ка, зависит в основном от воздушного зазора. В машинах, имеющих малый зазор, например в асинхронных двигателях, эта часть потока незначительна, и в расчетах ее не учитывают. В машинах с больши­ми зазорами увеличение расчетной длины воздушного зазора по сравнению с действительной за счет этой части потока принимается равным 2δ.

Рис. 4.3. Распределение индукции в Рис. 4.4. К расчету коэффициента

воздушном зазоре электрической машины воздушного зазора

по длине магнитопровода

Влияние провалов в кривой индукции, возникающих над радиальными вентиляционными

каналами, учитывается при определении l_δ с ледующим образом. Действительная ширина

радиальных каналов b_k заменяется расчетной b'_k, которая зависит от соотношения b_k/ δ.

Таким образом, расчетная длина магнитопровода в общем случае определяется по формуле

l_δ = l₁ - n_k b'_k + 2δ (4.8)

где l₁ – конструктивная длина магнитопровода; n_k и b'_k – соответственно число и расчетная ширина радиальных вентиляционных каналов.

При наличии каналов только на статоре (или только на роторе)

b'_k = (4.9)

При каналах на статоре, и на роторе

b'_k = (4.10)

Радиальные вентиляционные каналы обычно выполняются шириной b_k = 10 мм. В машинах с малым воздушным зазором (δ << b_k) расчетная ширина канала b'_k ≈ b_k.

В машинах с большим воздушным зазором (δ >> b_k) расчетная ширина канала b'_k ≈ 0.

С учетом рассмотренных особенностей распределения индукции в воздушном зазоре электрической машины расчетная площадь полюсного деления

S_δ = a_δ τ l_δ (4.11)

Тогда индукция в зазоре

B_δ = (4.12)

Магнитодвижущая сила воздушного зазора между гладкими по­верхностями

F_δ = 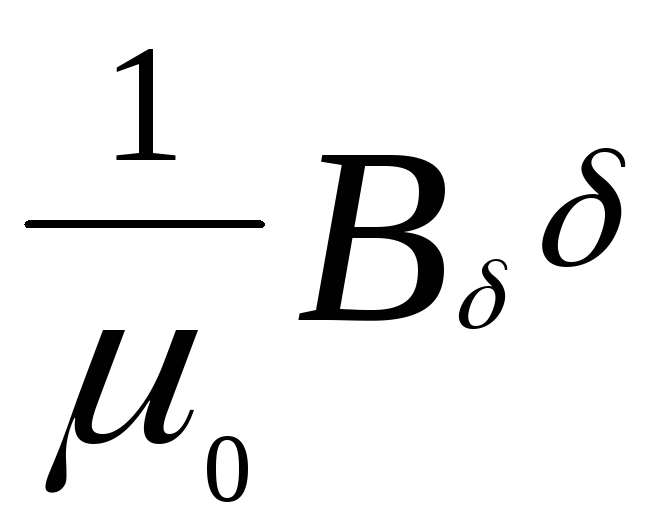(4.13)

В большинстве машин поверхности статора и ротора, ограничивающие воздушный зазор, не гладкие, а имеют различные неровно­сти: пазы, углубления для размещения бандажей и др. Магнитное сопротивление участков такого зазора в поперечном сечении маши­ны различно, поэтому распределение индукции по площади воздуш­ного зазора неравномерно. Наибольшая неравномерность возникает из-за наличия зубцов на статоре и роторе. Над коронками зубцов магнитные линии сгущаются, а над прорезями пазов плотность линии уменьшается (рис. 4.4). В кривой индукции в воздушном зазоре появляются провалы. Магнитное сопротивление и маг­нитное напряжение воздушного зазора при неравномерной индукции возрастают.

Увеличение магнитного напряжения учитывается введением ко­эффициента воздушного зазора (коэффициента Картера) k_δ. Этот коэффициент, полученный расчетом полей в зазорах с различным соотношением ширины зубцов и пазов, показывает, насколько воз­растает магнитное напряжение зазора при зубчатой поверхности статора или ротора по сравнению с магнитным напряжением зазора между гладкими поверхностями.

Можно использовать также понятие расчетного воздушного зазора

δ' = δ k_δ (4.13 а)

т. е. равномерного воздушного зазора, который имеет магнитную проводимость, равную магнитной проводимости реального воздуш­ного зазора. С учетом k_δ МДС зазора

F_δ = . (4.14)

Если одна поверхность зазора гладкая, а другая зубчатая, то k_δ достаточно точно определяется по формуле

k_δ = tz / (tz - γ_δ), (4.15)

где

либо по формуле

(4.16)

Обозначения величин, входящих в формулы, ясны из рис. 4.4.

Формула (4.15) получила наибольшее распространение. Форму­ла (4.16) используется, в основном, при открытых пазах.

Коэффициенты воздушного зазора рассчитывают отдельно для статора и для ротора. В первом случае предполагается, что поверх­ность статора зубчатая, а ротора — гладкая, во втором — наобо­рот: поверхность ротора зубчатая, а статора гладкая.

В расчетные формулы (4.14) — (4.16) подставляются значения t_z и b_ш, характеризующие зубцы, влияние которых учитывается коэф­фициентами k_δ1 и k_δ2. Так, для машины, имеющей зубцы и на стато­ре, и на роторе, рассчитывают:

для статора

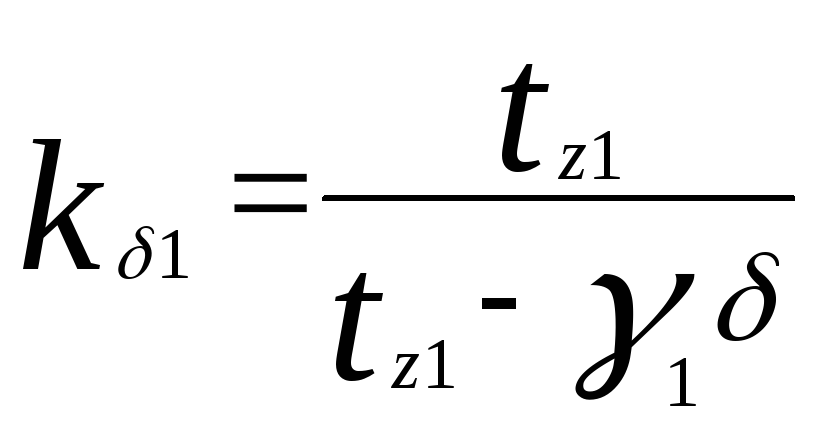; (4.17)

для ротора

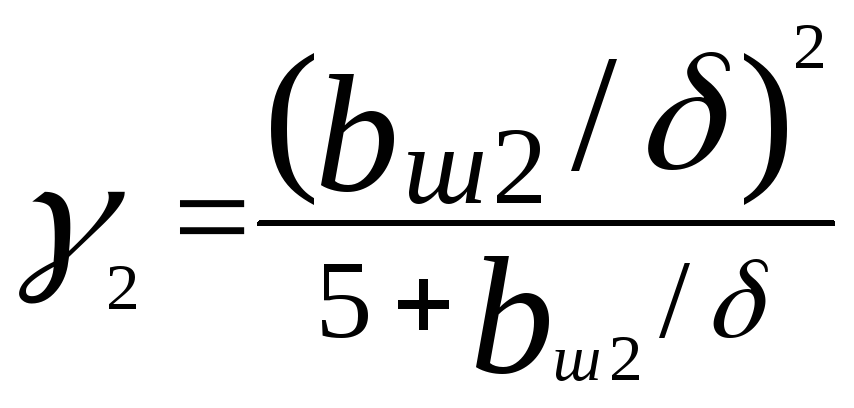; (4.18)

где t_z1, b_ш1 и t_z2 и b_ш2 — соответственно зубцовые деления и ширина шлица пазов статора и ротора.

По аналогичным формулам находят и другие частичные коэф­фициенты воздушного зазора k_δ3, k_δ4,..., учитывающие влияние дру­гих неравномерностей воздушного зазора, например канавок для размещения бандажей на якорях машин постоянного тока.

Результирующий коэффициент воздушного зазора равен произ­ведению всех частичных коэффициентов, рассчитанных для статора и ротора:

k_δ = k_δ1 k_δ2 k_δ3… (4.19)

Таким образом, МДС воздушного зазора электрической маши­ны F_δ, А, определяется по формуле

F_δ = 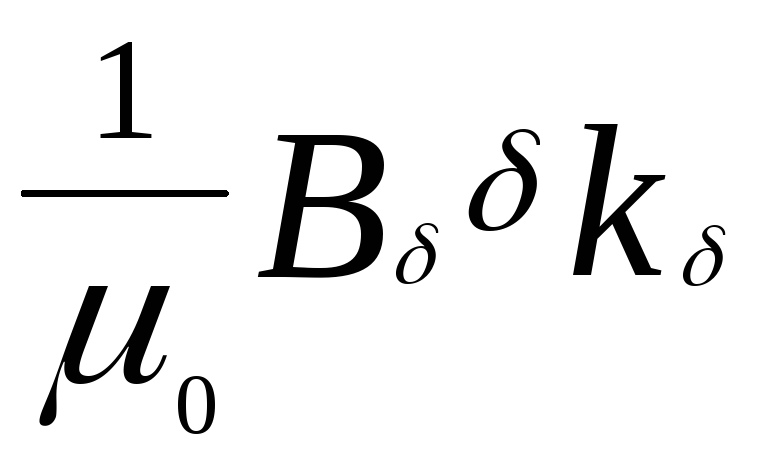, (4.20)

где k_δ — коэффициент воздушного зазора; В_δ — индукция в воздуш­ном зазоре, Тл:

В_δ = Ф/ ( a_δ τ l_δ ),

α_δ — коэффициент полюсного перекрытия; l_δ — расчетная длина магнитопровода [6].