Отчет 2

Министерство образования и науки Российской Федерации

ФГБОУ ВО «Кубанский государственный технологический

Университет»

кафедра электротехники и электрических машин

Математическое моделирование в электроэнергетике

Отчет по лабораторной работе №2

Интерполирование функций

Выполнил:

Студент группы 14-НБ-ЭЭ2

Дюков Владислав

Проверил:

Автайкин Илья Николаевич

Краснодар-2016

Целью работы является изучение методов и алгоритмов интерполирования функций и аппроксимации функции и реализации их в MathCad.

Содержание работы:

1. Исследование локальных методов интерполирования результатов эксперимента;

2.Иссследование глобальных методов интерполирования результатов эксперимента.

Перечень необходимых материалов, приборов, оборудования:

лабораторная работа проводится в компьютерном классе с сетевым оборудованием со следующим программным обеспечением: ОС MS Windows XP и выше, офисный пакет OpenOffice, система инженерных и математических расчетов MathCad.

Данна функция на интервале [-1;1]

1. Кусочно-постоянная интерполяция

Таблица 1.1 Для левой кусочно-постоянной интерполяции

Узел	0	1	2	3	4	5
xi	-0,5	-0,1	0,3	0,7	1,1	1,5
F(xi)	-2.482	0.65	1.593	1.878	1.963	1.989
Интервал	[-0,5; -0,1]	[-0,1; 0,3]	[0,3; 0,7]	[0,7; 1,1]	[1,1; 1,5]

Рисунок 1.1 Левая кусочно-постоянная интерполяция

Таблица 1.2 Для правой кусочно-постоянной интерполяции

Узел	0	1	2	3	4	5
xi	-0,5	-0,1	0,3	0,7	1,1	1,5
F(xi)	-2.482	0.65	1.593	1.878	1.963	1.989
Интервал		[-0,5; -0,1]	[-0,1; 0,3]	[0,3; 0,7]	[0,7; 1,1]	[1,1; 1,5]

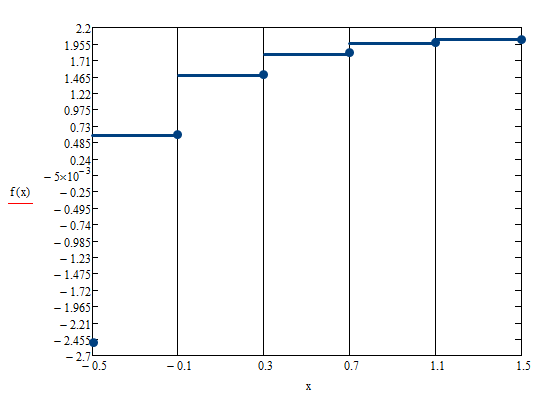
Рисунок 1.2 Правая кусочно-постоянна интерполяция

2. Кусочно-линейная интерполяция

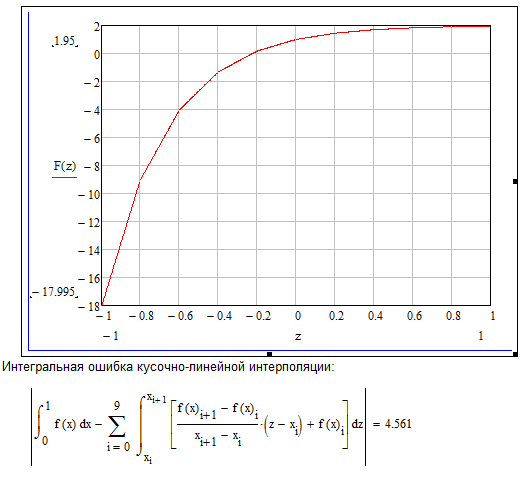
Рисунок 2.1 Кусочно-линейная интерполяция

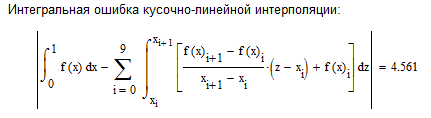
3. Кубический интерполяционный сплайн

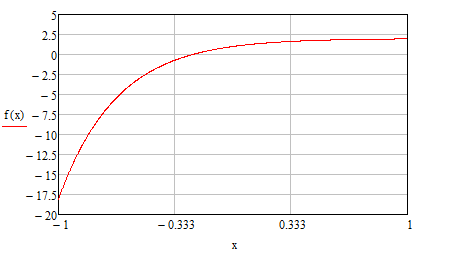
Рисунок 3.1 График заданной функции

Разобьем функцию на 3 отрезка

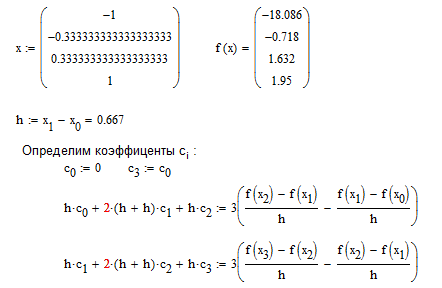
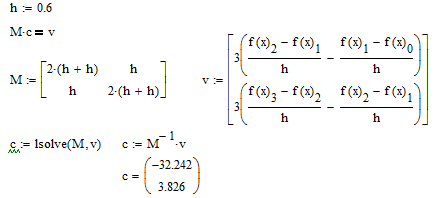
Рисунок 3.2 Кубический интерполяционный сплайн

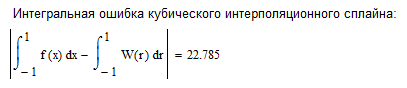
4. Интерполяционный многочлен Лагранжа

Рисунок 4.1 Интерполяционный многочлен Лагранжа второй степени

Рисунок 4.2 Интерполяционный многочлен Лагранжа второй степени

Рисунок 4.3 Интерполяционный многочлен Лагранжа четвертой степени

Рисунок 4.4 Интреполяционный многочлен Лагранжа восьмой степени

Заключение: в этой лабораторной работе мы изучили методы и алгоритмы интерполирования и аппроксимации функции и реализовали их в MathCad.