
Элементарные ФКП, Коши, вычеты степенные ряды
.docxЭлементарные функции комплексного переменного
Функции
комплексной переменной ![]() определяются
как суммы следующих рядов, сходящихся
во всей плоскости комплексного
переменного:
определяются
как суммы следующих рядов, сходящихся
во всей плоскости комплексного
переменного:
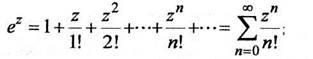 (1.4)
(1.4)
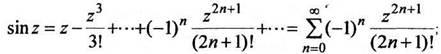 (1.5)
(1.5)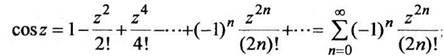 (1.6)
(1.6)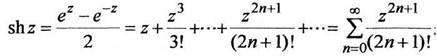 (1.7)
(1.7)
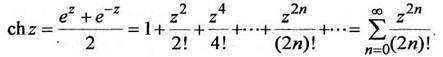 (1.8)
(1.8)
Из определения функций (10.4)-(10.8) следуют формулы, связывающие их:
![]() (1.9)
(1.9)
![]() (1.10)
(1.10)
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
![]() (1.13)
(1.13)
![]() (1.14)
(1.14)
![]() (1.15)
(1.15)
![]() (1.16)
(1.16)
Элементарные функции (1.4) – (1.8) являются однозначными и непрерывными на всей комплексной области Z.
2.
Показательная функция ![]() совпадает
с обычной функцией
совпадает
с обычной функцией ![]() для
нее справедлива теорема сложения
для
нее справедлива теорема сложения ![]()
Функция ![]() периодическая
с чисто мнимым основным периодом
периодическая
с чисто мнимым основным периодом
![]()
![]()
Тригонометрические
функции ![]() для
действительных
для
действительных ![]() совпадает
с обычным синусом и косинусом, периодичны
с действительным периодом
совпадает
с обычным синусом и косинусом, периодичны
с действительным периодом![]() -
нечетная,
-
нечетная, ![]() -
четная функция; подчиняются обычным
тригонометрическим соотношениям:
-
четная функция; подчиняются обычным
тригонометрическим соотношениям:
![]() и
т.п.
и
т.п.
Функция ![]() называется
гиперболическим синусом; функция
называется
гиперболическим синусом; функция ![]() называется
гиперболическим конусом. Гиперболические
функции
называется
гиперболическим конусом. Гиперболические
функции ![]() выражаются
через тригонометрические функции
формулами (1.15,1.16).
выражаются
через тригонометрические функции
формулами (1.15,1.16).
С помощью функций (1.4) - (1.8) вводятся другие элементарные функции. 3 Логарифмическая функция определяется как функция, обратная показательной:
если: ![]()
Для нее справедливо свойство логарифмов:
|
|
В
частности, полагая ![]() ,
получаем
,
получаем
![]() (1.17)
(1.17)
В формуле
(1.17) символ ![]() может
обозначать любое значение аргумента,
поэтому каждое комплексное число имеет
бесчисленное множество логарифмов.
может
обозначать любое значение аргумента,
поэтому каждое комплексное число имеет
бесчисленное множество логарифмов.
Выражение ![]() называется
главным значением логарифмической
функции и обозначается, как
называется
главным значением логарифмической
функции и обозначается, как ![]() Многозначная
логарифмическая функция обозначается
Многозначная
логарифмическая функция обозначается![]()
![]() (1.18)
(1.18)
4. Общая показательная функция:
![]() (1.19)
(1.19)
Эта
функция представляет собой совокупность
отдельных, не связанных между собой
однозначных функции, отличающихся
множителями ![]() где k- целое
число. Главное значение этой многозначной
функции равно
где k- целое
число. Главное значение этой многозначной
функции равно ![]()
где ![]() - произвольное
комплексное число.
- произвольное
комплексное число.
Полагая, ![]() ,
получаем
,
получаем ![]()
![]() (1.20)
(1.20)
где ![]() -
произвольное комплексное число.
-
произвольное комплексное число.
Полагая ![]() ,
получаем
,
получаем ![]()
![]() (1.21)
(1.21)
где k –
целое число. При ![]() функция
функция ![]() всегда
имеет бесконечно много значений.
всегда
имеет бесконечно много значений.
Если ![]() , то
получаем многозначную функцию - корень
n-й степени
, то
получаем многозначную функцию - корень
n-й степени ![]()
При ![]() имеем
частный случай однозначной степенной
функции
имеем
частный случай однозначной степенной
функции ![]()
К основным элементарным функциям комплексной переменной относится также дробно-рациональная функция и её частные случаи.
Дробно-рациональная функция:
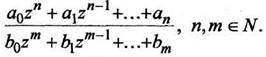 (1.22)
(1.22)
Частные случаи этой функции:
а)линейная
функция ![]() -
комплексные числа
-
комплексные числа
б)степенная
функция ![]()
в)дробно-линейная
функция 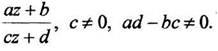
Производные функций комплексного переменного. Условия Коши-Римана.
Пусть
функция ![]() =u(x,y)+iv(x,y)
определена в окрестности точки z = x+iy.
Если переменной z придать
приращение z=x+iy,
то функция
=u(x,y)+iv(x,y)
определена в окрестности точки z = x+iy.
Если переменной z придать
приращение z=x+iy,
то функция ![]() получит
приращение
получит
приращение
= ![]() (z+z)–=u(x+x, y+y)+
(z+z)–=u(x+x, y+y)+
+ iv(x+x, y+y) - u(x,y) - iv(x,y) = [u(x+x, y+y) –
– u(x,y)] + i [v(x+x, y+y) - v(x,y)] =
=u(x,y) + iv(x,y).
Определение. Если существует предел
![]()
![]() =
= ![]()
![]() ,
,
то
этот предел называется производной от
функции в точке zи
обозначается черезf(z)
или![]() .
Таким образом, по определению,
.
Таким образом, по определению,
=![]() =.
(1.37)
=.
(1.37)
Если
функция имеет производную в точке z,
то говорят, что функция дифференцируема
в точкеz.
Очевидно, для дифференцируемости функции
необходимо, чтобы функцииu(x,y)
иv(x,y)
были дифференцируемы. Однако этого не
достаточно для существования
производнойf(z).
Например, для функцииw=![]() =x–iyфункцииu(x,y)=x
=x–iyфункцииu(x,y)=x
и v(x,y)=–yдифференцируемы
во всех точках M(x,y),
но предел отношения![]() приx0,y0
не существует, так как, еслиy =
0,x0,
тоw/z =
1,
приx0,y0
не существует, так как, еслиy =
0,x0,
тоw/z =
1,
если же x= 0,y0, тоw/z= -1.
Единого предела не существует. Это означает, что функция
w= не имеет производную ни в одной точкеz. Для существования производной от функции комплексного переменного требуются дополнительные условия. Какие именно? Ответ на этот вопрос дает следующая теорема.
Теорема.Пусть функцииu(x,y) иv(x,y) дифферен-цируемы в точке M(x,y). Тогда для того, чтобы функция
= u(x,y) + iv(x,y)
имела производную в точке z=x+iy, необходимо и достаточно, чтобы выполнялись равенства
![]() .
(1.38)
.
(1.38)
Равенства (1.38) называются условиями Коши-Римана.
Степенные ряды. Ряды Тейлора. Ряды Лорана.
степенным рядом называется ряд вида
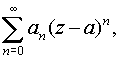
где а![]() Сz и
{an}
Сz и
{an}![]() Cz.
Cz.
Известно, что областью сходимости степенного ряда является круг {z: |z-a|<R}, радиус R которого можно определить по формуле

или по формуле
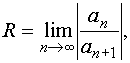 если
если 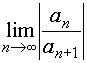 существует
(конечный или равный +
существует
(конечный или равный +![]() ).
Во всех внутренних точках круга сходимости
степенной ряд сходится абсолютно, во
внешних точках круга сходимости он
расходится.
).
Во всех внутренних точках круга сходимости
степенной ряд сходится абсолютно, во
внешних точках круга сходимости он
расходится.
Степенной ряд может сходиться или расходиться во всех или в некоторых точках окружности {z: |z–a|=R}.
Замечание. Степенной
ряд может сходиться только в точке z=a,
которую в этом случае считают кругом
сходимости с радиусом R=0.
Степенной ряд может сходится во всех
точках плоскости Cz,
которую в этом случае считают кругом
сходимости с радиусом R=+![]()
Внутри круга сходимости сумма степенного ряда является аналитической и однозначной функцией, причем на границе круга сходимости есть по крайней мере одна точка, в которой сумма ряда не является аналитической. Поэтому иногда радиус сходимости степенного ряда
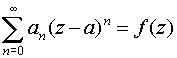
легче найти как расстояние от точки z=a до ближайшей к ней точки, в которой функция f (z) не является аналитической.
Степенной ряд
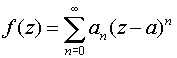
в круге сходимости радиуса R можно почленно дифференцировать и почленно интегрировать, т. е.
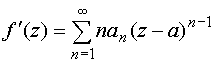 и
и 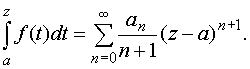
При этом радиусы сходимости полученных рядов будут также равны R.
Если функция w=f (z) является аналитической и однозначной в круге {z: |z-a|<R}, то она разлагается в этом круге в степенной ряд
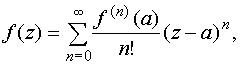
который называется рядом Тейлора для функции f (z).
При нахождении ряда Тейлора для функции f (z), как правило, затруднительно вычислить производные f (n)(а), поэтому рекомендуется пользоваться следующими стандартными разложениями функций в окрестностях точки z=0:
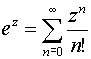 при
z
при
z![]() Cz;
Cz;
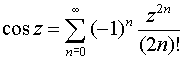 при z
при z![]() Cz;
Cz;
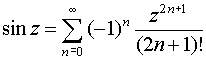 при
z
при
z![]() Cz;;
Cz;;
 при
z
при
z![]() Cz;;
Cz;;
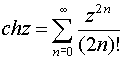 при
z
при
z![]() Cz;;
Cz;;
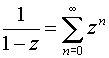 при
|z|<1.
при
|z|<1.
Если
функция w=f (z)
является аналитической и однозначной
в кольце {z: r<|z-a|<R},
где а![]() Сz;
0£ r<R
Сz;
0£ r<R![]()
![]() то
в указанном кольце справедливо разложение
в ряд
то
в указанном кольце справедливо разложение
в ряд
 ,
,
где 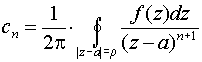 при n=0; ± 1; ± 2;...
и r<r <R.
при n=0; ± 1; ± 2;...
и r<r <R.
Этот ряд называется рядом Лорана для функции f (z), а ряды
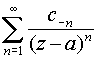 и
и 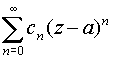 с
с
оответственно главной и правильной частями ряда Лорана.
На практике при нахождении ряда Лорана для функции f (z) используют приведенные ранее стандартные разложения элементарных функций в ряд Тейлора, применяя специальные приемы: известные формулы, дифференцирование и интегрирование стандартных разложений, представление рациональных функций в виде суммы простейших дробей.
Интеграл по комплексному переменному. Теорема Коши. Формула Коши.
Вычеты и их применение.
Вычеты и их применение
![]() -
вычет функции f(z) относительно
изолированной особой точки z0:
-
вычет функции f(z) относительно
изолированной особой точки z0:
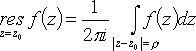
(в
круге ![]() нет
других особых точек).
нет
других особых точек).
Если 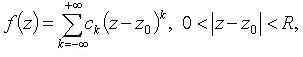 то
то
![]()
Вычисление вычетов
1. z0 - устранимая особая точка:
![]()
2. z0 - полюс:
а) z0 - простой полюс:
![]()
В
частности, если ![]() то
то
![]()
б) z0 - полюс порядка m:

(формула также верна, если z0 - полюс порядка не выше m).
3. z0 - существенно особая точка. Вычет находится по разложению в ряд Лорана.
