УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ.

1. Волновое уравнение для функции  :

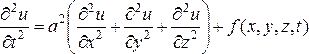 или  , (1)

где 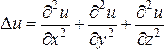 – оператор Лапласа.

Волновое уравнение относится к гиперболическому типу. Уравнение (1), например, описывает процесс распространение механических возмущений в сплошной среде.

В одномерном случае волновое уравнение

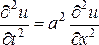
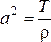называют уравнением колебаний струны. Это уравнение описывает свободные колебания струны без воздействия внешних сил. Функция  характеризует вертикальное перемещение струны,  ,  – натяжение струны,  – плотность материала струны.

2. Уравнение Лапласа для функции 

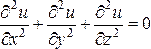 или  (2)

относится к уравнениям эллиптического типа. Этим уравнением, например, описывается стационарный процесс распределения тепла в однородной изотропной среде. Функция  – температура в точках среды.

Неоднородное уравнение

 (2’)

называется уравнением Пуассона.

3. Уравнение теплопроводности (уравнение диффузии) для функции  :

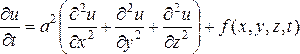 или  , (3)

относится к уравнениям параболического типа и описывает процесс распространения тепла в сплошной среде (а также лежит в основе математического моделирования диффузионных процессов)

Если в уравнениях (1), (3) в правой части функция  , то они называются однородными, если  , то уравнения (1) и (3) называются неоднородными.

Для полного описания того или иного физического процесса мало иметь только дифференциальное уравнение, надо ещё знать начальное состояние этого процесса (начальное условие) в виде

 (4)

или

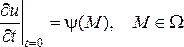 (5)

и режим на границе области (граничное условие) в виде

 (6)

или

 . (7)

Здесь приняты обозначения  – область, в которой происходит процесс,  – граница области,  – нормаль к границе области.

РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ОДНОМЕРНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ СТЕРЖНЯ БЕСКОНЕЧНОЙ ДЛИНЫ

В первую очередь рассмотрим задачу Коши дляоднородного уравнения теплопроводности.

 , (125)

удовлетворяющее неоднородному начальному условию

 . (126)

Начнем с того, что заменим переменные x и t на  и введем в рассмотрение функцию  . Тогда функции  будут удовлетворять уравнениям

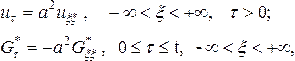
где  - функция Грина, определяемая формулой

 , (127)

и обладающая свойствами

 (128)

 (129)

 ; (130)

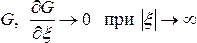 . (131)

Умножив первое уравнение на G*, а второе на и и затем сложив полученные результаты, получим равенство

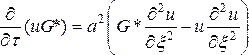 . (132)

После интегрирования по частям равенства (132) по  в пределах от -∞ до +∞ и по  в пределах от 0 до t, получим

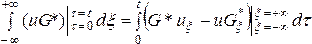 . (133)

Если предполагать, что функция  и ее производная  ограничены при  , то в силу свойств (131) интеграл в правой части (133) равен нулю. Следовательно, можно записать

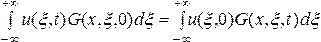 . (134)

Заменив в этом равенстве  на  , а  на  , получим соотношение

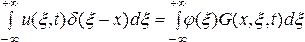
или

 .

Отсюда, используя формулу (127) окончательно получим

 . (135)

Формула (135) называется формулой Пуассона и определяет решение задачи Коши (125), (126) для однородного уравнения теплопроводности с неоднородным начальным условием.

Решение же задачи Коши для неоднородного уравнения теплопроводности

 , (136)

удовлетворяющее неоднородному начальному условию

 , (137)

представляет собой сумму решений:

 ,

где  является решением задачи Коши для однородного уравнения теплопроводности.  , удовлетворяющее неоднородному начальному условию  , а 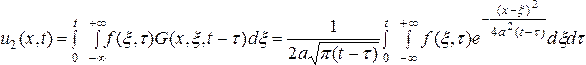 является решением  , удовлетворяющее однородному начальному условию  . Таким образом, решение задачи Коши (136), (137) определяется формулой

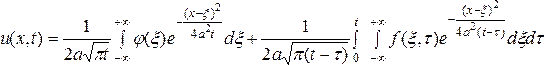 .(138)

РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ УРАВНЕНИЯ СТРУНЫ БЕСКОНЕЧНОЙ ДЛИНЫ

Решение уравнения свободных колебаний бесконечной струны.

Уравнение свободных колебаний бесконечной струны:

(без краевых условий)

решают при помощи формулы Даламбера:

Пример:

Решение: Имеем задачу свободных колебаний бесконечной струны (без краевых условий). Применяем формулу Даламбера:

=

.

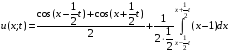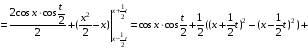
РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ УРАВНЕНИЯ СТРУНЫ НА КОНЕЧНОМ ОТРЕЗКЕ

Уравнение вида

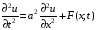(1)

с краевыми условиями

(2)

и начальными условиями

(3)

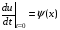(4)

описывает закон колебаний однородной тонкой нерастяжимой струны длины l, закрепленной на концах в точках х=0 и х=l (условия (2)), с начальной формой (х) (условие (3)) и начальной скоростью (х) (условие (4)), в поле действия внешней силы (например, силы тяжести, в магнитном поле и т.п.). Постоянный параметр a² зависит от свойств струны, функция F(x;t) - от внешней силы. Если F(x;t)=0 – это значит, что внешней силы нет (или ей можно пренебречь) и колебания называются свободными.

Отметим, что колебания рассматриваются малые (отклонение u точек струны от положения равновесия – оси Ох – мало), плоские (колебания происходят только в плоскости хOu), поперечные (каждая точка струны движется строго перпендикулярно положению равновесия).

Уравнение свободных колебаний струны, закрепленной на концах:

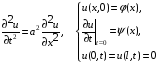
имеет решение вида

,

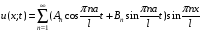где коэффициенты А_n и В_n находят из начальных условий:

подставляя t=0 получаем

,

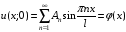то есть А_n – коэффициенты Фурье для функции (х) при разложении на интервале (0; l) по синусам кратных дуг.

Далее, дифференцируя u(х;t) по t и подставляя t=0 получаем:

,

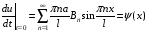то есть 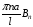– коэффициенты Фурье для функции (х) при разложении на интервале (0; l) по синусам кратных дуг.

Напомним, что коэффициенты Фурье в общем случае вычисляются при помощи интегралов (см. тему «Ряд Фурье», с.38), а иногда их можно подобрать (если раскладываемая функция представляет собой сумму синусов кратных дуг).