
Ряды
.docxОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ И ОБОБЩЕННЫЕ РЯДЫ ФУРЬЕ
МАТЕМАТИЧЕСКИОЕ ОПИСАНИЕ МЕТОДОВ СПЕКТРАЛЬНОГО РАЗЛОЖЕНИЯ СИГНАЛОВ
Бесконечная система действительных ненулевых функций
![]() (2.1)
(2.1)
называется ортогональной на отрезке [a,b], если
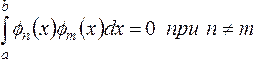 (2.2)
(2.2)
Это условие (2.2) выражает попарную ортогональность функций системы (2.1).
Интервал [a,b] называется интервалом ортогональности системы функций.
Величина
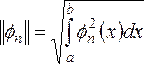 (2.3)
(2.3)
называется нормой функции ![]() .
.
Функция ![]() ,
для которой выполняется условие
,
для которой выполняется условие
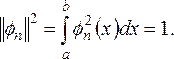 (2.4)
(2.4)
называется нормированной функцией, а система нормированных функций (2.1), для двух функций которой выполняется условие ортогональности (2.2), называетсяортонормированной системой.
Доказано,
что если функции ![]() ,
то произвольная кусочно-непрерывная
функция
,
то произвольная кусочно-непрерывная
функция ![]() ,
для которой выполняется условие:
,
для которой выполняется условие:
![]() (2.5)
(2.5)
может быть представлена в виде суммы ряда
![]() (2.6)
(2.6)
Коэффициенты ряда (2.6) определяются по формуле:
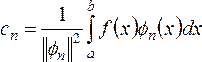 (2.7)
(2.7)
Таким
образом, ряд (2.6), в котором
коэффициенты ![]() определяются
по (2.7), называется обобщённым рядом
Фурье по данной системе
определяются
по (2.7), называется обобщённым рядом
Фурье по данной системе ![]() .
Совокупность коэффициентов
.
Совокупность коэффициентов ![]() называется спектром сигнала
в данной ортогональной системе и
полностью определяется этот сигнал.
называется спектром сигнала
в данной ортогональной системе и
полностью определяется этот сигнал.
Обобщённый
ряд Фурье обладает следующим важным
свойством: при заданной системе функций ![]() и
фиксированном числе слагаемых ряда
(2.6) он обеспечивает наилучшую аппроксимацию
(в смысле минимума среднеквадратической
ошибки) данной функции
и
фиксированном числе слагаемых ряда
(2.6) он обеспечивает наилучшую аппроксимацию
(в смысле минимума среднеквадратической
ошибки) данной функции ![]() .
Это означает, что среднеквадратическая
ошибка, под которой подразумевается
величина
.
Это означает, что среднеквадратическая
ошибка, под которой подразумевается
величина
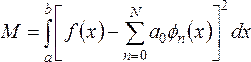 (2.8)
(2.8)
достигает
минимума, когда коэффициенты ряда ![]()
Из этого факта следует фундаментальное соотношение, справедливое для любой ортогональной системы, называемое неравенством Бесселя:
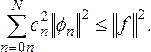 (2.9)
(2.9)
Ортогональная система называется полной, если увеличение числа членов ряда позволяет сделать среднеквадратическую ошибку М (2.8) сколь угодно малой. Условие полноты можно записать в виде соотношения:
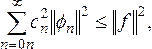 (2.10)
(2.10)
называемого теоремой Парсеваля. При выполнении условия (2.10) можно считать, что ряд (2.6) сходится в среднем:
![]() (2.11)
(2.11)
Из этого,
однако, ещё не следует, что ряд сходится
к ![]() при
любых значениях x.
при
любых значениях x.
Основной
практический интерес представлю полные
ортонормированные системы функций,
поскольку неполные системы не дают
сходимости разложения для всех квадратично
интегрируемых функций. Но, несмотря на
это, некоторые неполные системы также
находят применение. Например, выходное
напряжение идеального фильтра нижних
частот может быть точно представлено
путём разложения в ряд по неполной
ортогональной системе функций вида 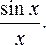
ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ. УСЛОВИЯ РАЗЛОЖИМОСТИ ФУНКЦИИ В РЯД ФУРЬЕ.
Тригонометрическим
рядом Фурье для функции f(x) на интервале
от ![]()
называется ряд вида:
![]() ,
где
,
где
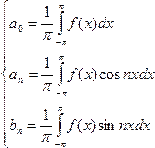
Условия разложимости:
Пусть f(x):
1)
Периодическая с ![]()
2) Кусочномонотонна
3)
Ограничена на ![]() функцию
f(x) можно разложить в ряд Фурье на
функцию
f(x) можно разложить в ряд Фурье на ![]() ,
который сходится к этой функции во всех
точках непрерывности, в точках разрыва
сумма ряда равна полусумме левого и
правого предела функции.
,
который сходится к этой функции во всех
точках непрерывности, в точках разрыва
сумма ряда равна полусумме левого и
правого предела функции.
Замечание:Основная трудность построения рядов Фурье в вычислении интегралов.

РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ПО СИНУСАМ ИЛИ ПО КОСИНУСАМ.
Если
функция ![]() четная (т.е.
четная (т.е. ![]() ), то
все её коэффициенты
), то
все её коэффициенты ![]() ,
и ряд Фурье имеет вид
,
и ряд Фурье имеет вид
![]() ,
,
где ![]() ,
, ![]() .
.
Если
функция ![]() нечетная (т.е.
нечетная (т.е. ![]() ), то
все коэффициенты
), то
все коэффициенты ![]() ,
и её ряд Фурье имеет вид
,
и её ряд Фурье имеет вид
![]() ,
,
где ![]() .
.
Определение. Эти ряды называются неполными тригонометрическими рядами, или рядами по косинусам и по синусам соответственно.
Разложение в ряд Фурье функций произвольного периода 2l
Пусть
функция ![]() определена
на отрезке
определена
на отрезке ![]() и
удовлетворяет на этом отрезке условиям
теоремы Дирихле. Введем новую переменную
по формуле
и
удовлетворяет на этом отрезке условиям
теоремы Дирихле. Введем новую переменную
по формуле ![]() и
рассмотрим функцию
и
рассмотрим функцию ![]() .
Функция
.
Функция ![]() определена
на отрезке
определена
на отрезке ![]() и
удовлетворяет теореме Дирихле. Ее ряд
Фурье имеет вид:
и
удовлетворяет теореме Дирихле. Ее ряд
Фурье имеет вид:
![]() ,
,
где ![]() .
.
Вернемся
к старой переменной ![]() .
.
Определение.
Ряд ![]()
с коэффициентами, вычисляемыми по формулам
![]() ,
, ![]() ,
, ![]()
называется рядом
Фурье для функции ![]() с
периодом
с
периодом ![]() .
.
Замечание.Если ![]() на
отрезке
на
отрезке ![]() четная, то
ее ряд Фурье имеет вид:
четная, то
ее ряд Фурье имеет вид: ![]() ,
где
,
где ![]() ,
, ![]() ;
;
Если ![]() - нечетная функция,
то
- нечетная функция,
то ![]() ,
,
где ![]() ,
, ![]() .
.
ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ.
Ряд Фурье очень компактно записывается в комплексном виде, если воспользоваться формулами Эйлера:
![]() .
.
Подставив это в формулу (22), сделаем ряд преобразований:
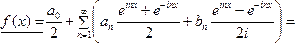
![]()
![]() ,
,
где ![]() .
.
Если вспомнить, как определяются через функцию f(x) коэффициенты Фурье an и bn (формулы (20), (21)), то комплексные коэффициенты Фурье (комплексные амплитуды) окажутся равными
![]() .
.
Если функция имеет период не 2p, а 2l, то по аналогии с формулой (23) получим
![]() ,
,
где ![]() .
.
В данном
представлении экспоненты с мнимым
показателем степени ![]() являются пространственными (если х -
координата) или временными (если х -
время)гармониками.
Множитель
являются пространственными (если х -
координата) или временными (если х -
время)гармониками.
Множитель ![]() называется
соответственно волновым
числом (k)
или циклической
частотой (w).
Совокупность чисел
называется
соответственно волновым
числом (k)
или циклической
частотой (w).
Совокупность чисел ![]() -
это соответственнопространственный
или частотный спектр,
который является дискретным.
-
это соответственнопространственный
или частотный спектр,
который является дискретным.
Если функция непериодическая, то можно считать, что для неё l ® ¥. Для этого случая преобразуем комплексные амплитуды таким образом:
![]() ,
где
,
где ![]() .
.
При
очень больших l и
изменении n на
единицу k изменится
на очень небольшую величину ![]() .
Обозначим левую часть равенства
через с(k)
=
.
Обозначим левую часть равенства
через с(k)
= ![]() .
В результате получим
.
В результате получим ![]() .
При этом сама функция преобразуется
так:
.
При этом сама функция преобразуется
так:
![]() .
.
Теперь в интеграле волновое число k (или частота w) принимает уже не дискретные значения, а меняется непрерывно. Величина с(k) называется непрерывным спектром волновых чисел (пространственный спектр). Соответственно, если независимая переменная - время, то с(w) называется частотным спектром.
В дифференциальных уравнениях используется преобразование Лапласа:
![]() .
.
В теории рядов есть похожее преобразование Фурье:
![]()
и обратное преобразование Фурье:
![]() .
.
ИНТЕГРАЛ ФУРЬЕ
Всякая
функция ![]() которая
на отрезке
которая
на отрезке ![]() удовлет-
воряет условиям разложимости в ряд
Фурье, может быть на этом отрезке
представлена тригонометрическим рядом
удовлет-
воряет условиям разложимости в ряд
Фурье, может быть на этом отрезке
представлена тригонометрическим рядом
![]() (1)
Коэффициенты
(1)
Коэффициенты ![]() ряда
(1) вычисляются по формулам
ряда
(1) вычисляются по формулам
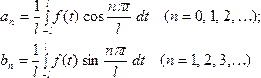 (2)
(2)
Ряд в
правой части равенства (1) можно записать
в другой форме. С этой целью внесём в
него из формул (2) значения коэффициентов ![]() ,
подведём под знаки интегралов
,
подведём под знаки интегралов ![]() и
и ![]() (это
возможно, поскольку переменной
интегрирования является
(это
возможно, поскольку переменной
интегрирования является ![]() )
и используем формулу для косинуса
разности. Будем иметь:
)
и используем формулу для косинуса
разности. Будем иметь:
![]() .
(3)
.
(3)
Если
функция ![]() первоначально
была на интервале числовой оси, большем,
чем
первоначально
была на интервале числовой оси, большем,
чем ![]() (например
на всей оси), то разложение (3) воспроизведёт
значение этой функции на отрезке
(например
на всей оси), то разложение (3) воспроизведёт
значение этой функции на отрезке ![]() и
продолжит её на всю числовую прямую,
как периодическую функцию, с пери
-одом
и
продолжит её на всю числовую прямую,
как периодическую функцию, с пери
-одом ![]() .
Поэтому, если функция
.
Поэтому, если функция ![]() (вообще
говоря, непериодическая) определена на
всей числовой оси, в формуле (3) можно
перейти к пределу при
(вообще
говоря, непериодическая) определена на
всей числовой оси, в формуле (3) можно
перейти к пределу при ![]() .
При этом естественно потребовать
выполнения следующих условий:
.
При этом естественно потребовать
выполнения следующих условий:
1). ![]() удовлетворяет
условиям разложимости в ряд Фурье на
любом конечном отрезке оси Ох;
удовлетворяет
условиям разложимости в ряд Фурье на
любом конечном отрезке оси Ох;
2).
Функция ![]() абсолютно
интегрируема на всей чис -ловой оси,
абсолютно
интегрируема на всей чис -ловой оси,
![]() (4)
(4)
При
выполнении условия 2) первое слагаемое
правой части равенства (3) при ![]() стремится
у нулю. В самом деле,
стремится
у нулю. В самом деле,
![]()
Попытаемся
установить, во что перейдёт в пределе
при ![]() сумма
в правой части (3). Положим
сумма
в правой части (3). Положим
![]()
![]()
так,
что ![]() .
Тогда сумма в правой части (3) примет вид
.
Тогда сумма в правой части (3) примет вид
![]() .
(5)
.
(5)
В силу
абсолютной сходимости интеграла, эта
сумма, при больших ![]() ,
мало отличается от выражения
,
мало отличается от выражения
![]()
которое
напоминает интегральную сумму для
функции пере -менного ![]()
![]()
составленную
для интервала ![]() изменения
изменения ![]() .
Поэтому естественно ожидать, что ,
при
.
Поэтому естественно ожидать, что ,
при ![]() ,
(
,
( ![]() сумма
(5) перейдёт в интеграл
сумма
(5) перейдёт в интеграл
![]()
С другой
стороны, при ![]() (
( ![]() фиксировано)
из фор -мулы (3) вытекает, что
фиксировано)
из фор -мулы (3) вытекает, что
![]() ,
(6)
,
(6)
и мы получаем равенство
![]() .
(7)
.
(7)
Достаточное условие справедливости формулы (7) выражается следующей теоремой
ТЕОРЕМА
1. Если функция ![]() абсолютно
интегрируема на всей числовой оси
абсолютно
интегрируема на всей числовой оси ![]() и
имеет вместе со своей производной
конечное число точек разрыва первого
рода на любом отрезке
и
имеет вместе со своей производной
конечное число точек разрыва первого
рода на любом отрезке ![]() ,
то справедливо равенство
,
то справедливо равенство
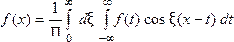
При этом
во всякой точке ![]() ,
являющейся точкой разрыва 1-го рода
функции
,
являющейся точкой разрыва 1-го рода
функции ![]() ,
значение интеграла в правой части (7)
равно
,
значение интеграла в правой части (7)
равно ![]()
Формулу (7) называют интегральной формулой Фурье, а стоящий в её правой части интеграл - интегралом Фурье. Если воспользоваться формулой для косинуса разности, то формулу (7) можно записать в виде
![]() ,
(8) где
,
(8) где
![]() (9)
(9)
Функции ![]() являются
аналогами соответствующих ко - эффициентов
Фурье
являются
аналогами соответствующих ко - эффициентов
Фурье ![]() и
и ![]()
![]() -
периодической функции, но последние
определены для дискретных значений
-
периодической функции, но последние
определены для дискретных значений ![]() ,
в то время как
,
в то время как ![]() определены
для непрерывных значений
определены
для непрерывных значений ![]() .
.
ИНТЕГРАЛ ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ
Предполагая ![]() абсолютно
интегрируемой на всей оси Ох, рассмотрим
интеграл
абсолютно
интегрируемой на всей оси Ох, рассмотрим
интеграл
![]() .
.
Этот
интеграл равномерно сходится для ![]() ,
так как
,
так как ![]() и
потому представляет собой не- прерывную
и, очевидно, нечётную функцию от
и
потому представляет собой не- прерывную
и, очевидно, нечётную функцию от ![]() .
Но тогда
.
Но тогда ![]() С
другой стороны, интеграл
С
другой стороны, интеграл
![]()
является
чётной функцией от переменной ![]() ,
так что
,
так что ![]() Следовательно,
интегральную формулу Фурье можно
записать так
Следовательно,
интегральную формулу Фурье можно
записать так
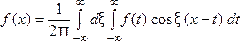 .
(10)
.
(10)
Умножим равенство
![]()
на мнимую
единицу ![]() и
прибавим к равенству (10). Получим
и
прибавим к равенству (10). Получим ![]() Отсюда,
в силу формулы Эйлера (
Отсюда,
в силу формулы Эйлера ( ![]() ),
будем иметь
),
будем иметь ![]()
(11)
Это комплексная
форма интеграла
Фурье. Здесь внешнее ин- тегрирование
по ![]() понимается
в смысле главного значения по Коши
понимается
в смысле главного значения по Коши![]()
