ОРИГИНАЛ И ЕГО ИЗОБРАЖЕНИЕ ПО ЛАПЛАСУ.

Функцией- оригиналом - называют функцию действительного аргумента

удовлетворяющую условиям:

1) для всех отрицательных значений аргумента функция тождественно равна нулю, т.е.

2) функция при возрастает не быстрее показательной функции, т.е. существ.уют такие постоянные что

3) на любом конечном отрезке положительной полуоси функция  и ее производные достаточно высокого порядка непрерывны или имеют конечное число разрывов 1-го рода.

Простейшей функцией - оригиналом является единичная функция Хевисайда

(1)

Если функция не удовлетворяет условию то произведение уже ему удовлетворяет, т.е. будет оригиналом.

Для простоты записи множитель опускается, например, пишут вместо вместо и т.д.

Изображением функции по Лапласу (преобразованием по Лапласу) называют функцию комплексной переменной определяемую соотношением

(2)

Интеграл (1.2) называют интегралом Лапласа.

Функция определяется в полуплоскости и является в этой области аналитической функцией.

То, что функция комплексной переменной является изображением по Лапласу функции действительного аргумента обозначается или

Изображение элементарных функций получается непосредственно с помощью интеграла (2).

Пример 1 Найти изображение по Лапласу функции 

РЕШЕНИЕ

 

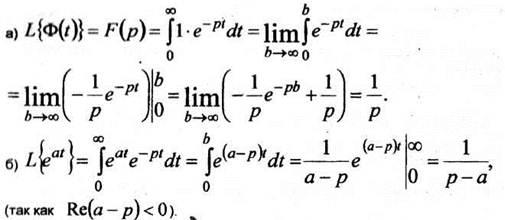
Таким образом, получаем

Преобразование, основанное на интеграле Лапласа (2), обладает линейными свойсгыами.

1. Преобразование суммы функций равно сумме преобразований этих функций

2 Постоянный множитель можно выносить за знак преобразования:

Из этих двух свойств следует, что линейной комбинации оригиналов соответствует линейная комбинация их преобразований:

 

(3)

Пример 2. Найти изображение функции 

РЕШЕНИЕ

Используем формулу (2) для функции Тогда

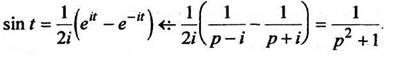
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА

1. Теорема подобияЕсли то для любого постоянногоа > 0

 

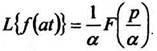(4)

Пример 3. НайдемИз примера2 _.По Формуле (4)

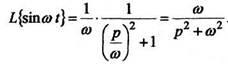
2.Дифференцирование оригиналаЕсли то

(5)

Методом индукции на основании формулы (5) получены формулы изображения высших производных:

 

(6)

 

(7)

 

(8)

Пример 4. ОпределимТак как 

то по формуле (5) получим:

3. Дифференцирование изображения.Если то т.е. дифференцирование изображения сводится к умножению на оригинала. В общем случае,

(9)

Пример 5. Определить изображения функций 

РЕШЕНИЕ

Так как 

В общем случае 

4. Интегрирование оригинала.Интегрирование оригинала сводится к делению изображения на р:

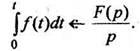(10)

Пример 6. Найти изображение функци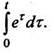 

РЕШЕНИЕ Так как то по формуле (10)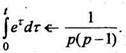 

 

5. Интегрирование изображения.Интефирование изображения равносильно делению на tоригинала (если существует конечный предел 

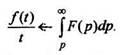(11)

Пример 7. Найдем изображение функции 

Так как 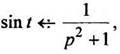то по формуле (11) получаем

6. Теорема смещенияПри умножении оригинала на изображение получается смещение аргумента на 

(12)

Пример 8. В примерах 3, 4, 5 найдены изображения функций По формуле (12) находим:

7. Теорема запаздывания."Включение" оригинала с запаздыванием на равносильно умножению изображения на 

(13)

В данной формуле важно подчеркнуть, что функция поэтому она умножена на единичную функцию Хевисайда с запаздыванием .График единичной функции Хевисайда с запаздывающим аргументом показан на рисунке 1.

Изображение 

 

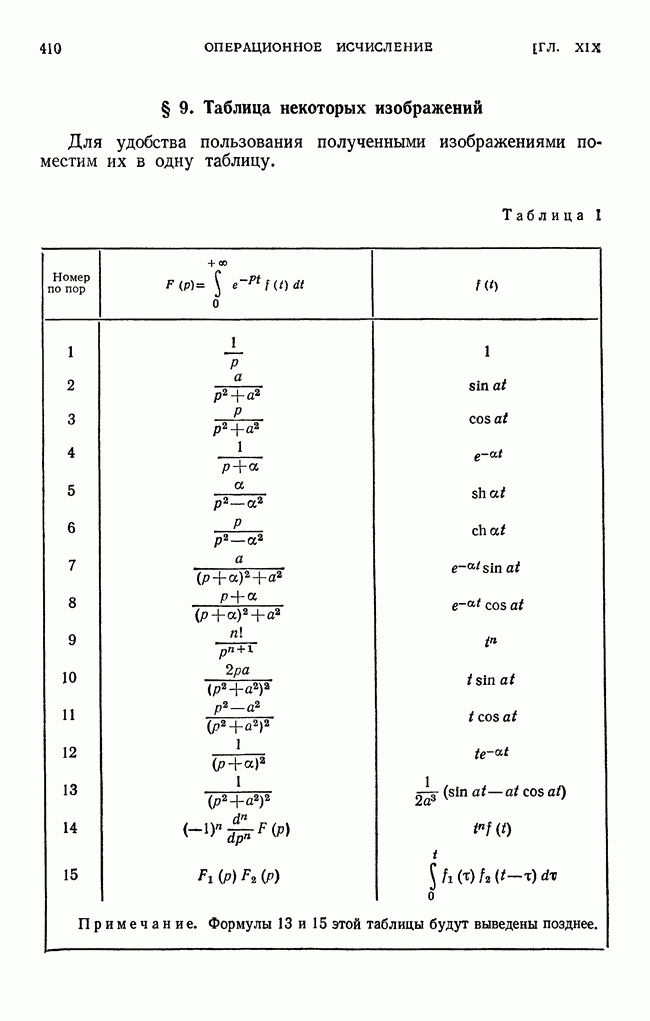
 ТАБЛИЦА ОРИГИНАЛОВ И ИЗОБРАЖЕНИЙ.

СВЁРТКА ОРИГИНАЛОВ И ЕЁ ПРИМЕНЕНИЕ. ТЕОРЕМА БОРЕЛЯ.

Свертка односторонних функций, ее свойства. Теорема Бореля

Сверткой функций  и , заданных на , называется функция, равная интегралу 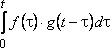, ; она обозначается , т.е.

, .  (21)

Свойства свертки 

1. Симметрия, т.е. .

В самом деле, изменяя порядок интегрирования и полагая , получаем равенство

.

2. Если  и  – оригиналы, то и их свертка также является оригиналом с показателем роста, равным наибольшему из показателей роста функций   и . Рекомендуем доказать самостоятельно это утверждение или же посмотреть в [3].

ПРИМЕР 32. Найти свертку функций  и .

Решение. 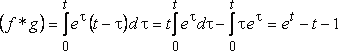, здесь ко второму интегралу применено интегрирование по частям.

Теорема Бореля

Если функции  и  – оригиналы и ,  и , , то произведение изображений  является изображением свертки соответствующих оригиналов для :

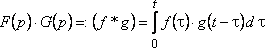.  (22)

В самом деле, по определению изображения имеем

.

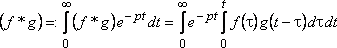Замечаем, что справа стоит двойной интеграл с областью интегрирования , изображенной на рисунке. Изменяя в этом интеграле порядок интегрирования, получаем

.

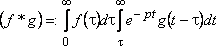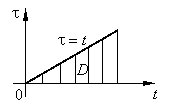
Замена переменной интегрирования  позволяет записать

.

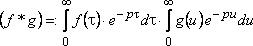Поскольку внутренний интеграл не зависит от , а внешний от , то двойной интеграл равен произведению двух интегралов, т.е.

.

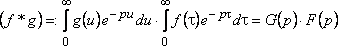Теорема Бореля применяется для нахождения оригинала в случае, когда изображение представлено в виде двух множителей, для каждого из которых оригинал устанавливается.

 ПРИМЕНЕНИЕ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ДЛЯ РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ  КОЭФФИЦИЕНТАМИ

Пусть имеем линейное неоднородное уравнение с постоянными коэффициентами:

где функция удовлетворяет условиям, налагаемым на оригиналы.

Уравнение (38) надо решить при нулевых начальных условиях

Применяя к обеим частям уравнения (38) преобразование Лапласа и учитывая начальные условия, найдем согласно (12):

,

откуда

.

Из равенства (40), пользуясь известными приемами операционного исчисления, рассмотренными выше, найдем по изображению  оригинал , который и будет являться искомым решением уравнения (38) при .

Если уравнение (40) требуется решить при ненулевых начальных условиях

,

то после применения к (40) преобразования Лапласа найдем согласно (11): 

или

где  известная целая рациональная функция от .

откуда определим оригинал , являющийся искомым решением уравнения (38).

Нетрудно видеть, что в случае однородного уравнения

ПРИМЕНЕНИЕ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ДЛЯ РЕШЕНИЯ  СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С  ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.

оставим  систему  уравнений:

 

 

Решив  ее,  получаем

 

 

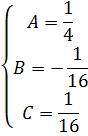
Итак  X(p)=  ,  откуда 

x(t)=—  решение  данного  дифференциального  уравнения.

Системы  линейных  дифференциальных  уравнений  с  постоянными  коэффициентами  можно  решать  операционными  методами  совершенно  так  же,  как  и  отдельные  уравнения;  все  отличие  заключается  лишь  в  том,  что  вместо  одного  изображающего  уравнения  приходим  к  системе  таких  уравнений,  причем  система  эта  в  отношении  изображений  искомых  функций  будет  линейно  алгебраической.  При  этом  никаких  предварительных  преобразований  исходной  системы  дифференциальных  уравнений  производить  не  требуется  [3,  с.  134].