
Voprosy_SGM
.docxCпец. главы математики, (2016г.) 4 семестр (преподаватель Братчиков А.В.)
ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ И ОБОБЩЕННЫЕ РЯДЫ ФУРЬЕ.
ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ. УСЛОВИЯ РАЗЛОЖИМОСТИ ФУНКЦИИ В РЯД ФУРЬЕ.
РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ПО СИНУСАМ ИЛИ ПО КОСИНУСАМ.
ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ.
ИНТЕГРАЛ ФУРЬЕ.
ИНТЕГРАЛ ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ.
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ.
Интегралы Гаусса и Пуассона.
РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ОДНОМЕРНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ СТЕРЖНЯ БЕСКОНЕЧНОЙ ДЛИНЫ.
РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ УРАВНЕНИЯ СТРУНЫ БЕСКОНЕЧНОЙ ДЛИНЫ.
РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ УРАВНЕНИЯ СТРУНЫ НА КОНЕЧНОМ ОТРЕЗКЕ.
ОРИГИНАЛ И ЕГО ИЗОБРАЖЕНИЕ ПО ЛАПЛАСУ.
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
ТАБЛИЦА ОРИГИНАЛОВ И ИЗОБРАЖЕНИЙ.
ИЗОБРАЖЕНИЕ ПРОИЗВОДНЫХ.
СВЁРТКА ОРИГИНАЛОВ И ЕЁ ПРИМЕНЕНИЕ. ТЕОРЕМА БОРЕЛЯ.
ПРИМЕНЕНИЕ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ДЛЯ РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.
ПРИМЕНЕНИЕ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.
Элементарные функции комплексного переменного.
Производные функций комплексного переменного. Условия Коши-Римана.
Степенные ряды. Ряды Тейлора. Ряды Лорана.
Интеграл по комплексному переменному. Теорема Коши. Формула Коши.
Вычеты и их применение.
Нахождение корней функций методом деления отрезка пополам, методами хорд и касательных.
Нахождение корней функций методом итераций. Сходимость.
Решение задачи Коши для ДУ первого порядка: метод Эйлера.
ЗАДАЧИ.
Разложить
в ряд Фурье заданную функцию. Определить
значения суммы ряда на концах отрезка
и построить её график: a)
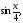
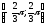 ,
b)
,
b)
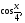
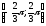 .
.
Найти
общее решение дифференциального
уравнения в частных производных a)
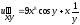 ;
;
b)
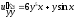 .
Здесь u=
u(x,y).
.
Здесь u=
u(x,y).
Найти закон движения бесконечной струны:
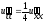 ,
-∞ <x<∞,
0<t<∞,
,
-∞ <x<∞,
0<t<∞,
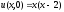 ,
,
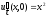 .
.
Найти решение задачи Коши уравнения теплопроводности для неограниченного стержня:
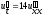 ,
,
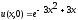
Найти
изображение функций
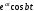 ,
,
 .
.
Найти оригинал функции: a)
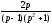 ;b)
;b)
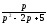 ;c)
;c)
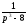 .
.
Найти
свертку функций
 и
и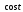 и её изображение.
и её изображение.
Решить операционным методом задачи Коши:
a)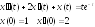 ;
b)
;
b)

Дана функция w= exp (z). Найти её значение: при а) z=iπ/2; b) z=π(2+i); c) z=1+(π/2+ 2πk)i.
Найти Ln (1+2i), Arcsin i , cos(i/2), sin (i).
Решить уравнение cos z =2, sin z = 3.
Является ли дифференцируемой функция f(z)=iexp(x) sin(y)+exp(x)cos(y). Если да, то найти f’(z), z=x+iy.
Вычислить интеграл от функции f(z)= z вдоль отрезка прямой соединяющего точки z =1 и z=i.
Вычислить
интеграл от функции f(z)=
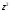 по ломаной OAB
с вершинами в точках z=0,
z=1,z=1+i
соответственно.
по ломаной OAB
с вершинами в точках z=0,
z=1,z=1+i
соответственно.
Найти
область сходимости ряда:
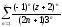
Разложить
функцию в ряд по степеням z-
z0 и указать область
сходимости полученного ряда: а)
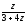 ,
z0=0; б)
,
z0=0; б)
 , z0=2.
, z0=2.
Разложить
функцию
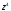 в ряд по степеням z- 2i.
в ряд по степеням z- 2i.
Вычислить
интеграл от функции
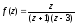 по окружностям : a)
|z-i|
= 7; b)
|z|=0,5;
по окружностям : a)
|z-i|
= 7; b)
|z|=0,5;
c) |z-1| =2,5, проходящих в положительном направлении.
Решить
приближенно методом деления отрезка
пополам
 .
.
Решить
приближенно методами хорд и касательных
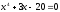 .
.
Решить
приближенно методом итераций
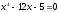 .
.
