
шпоры математика
.docx1. Предмет и метод теории вероятностей. ТВ – это матем. наука, изуч. закон-сти массовых случ. явл-й (событий, величин, функций, процессов и др.). Она опред. и анализ. числ. хар-ки случ. событий (объектов), наиболее важными из кот-х явл. вер-сть события и мат. ожид-е случ. вел-ны. Отправным понятием ТВ явл. исслед-е исходов, рез-ов случ. эксперимента (осущест-я комплекса условий). При этом исходы опыта случайны, т. е. заранее не известны. Осн. треб-ем к такому экспер-ту явл. возм-сть его повторить, т.е. не менять комплекс усл-й при повторном осущ-и опыта неогранич. число раз. В этих усл-ях должна наблюдаться закон-сть, проявл. в устойчивости частости (доли) появления опред. случ. исхода испыт-я, наблюд-я. ТВ с помощью мат. модели случ. эксп-нта опред. такие соотн-я между вер-стями разл. случ. событий (относ. к данному эксп-нту), кот-е позвол. вычислять вер-сти более сложных событий по вероятностям простых. Итак, предметом ТВ явл. изуч-е вероятностных законом-стей массовых однор. случ. событий. Методы ТВ широко примен. в разл. отраслях естествозн-я и техники: в теории надежности, теории массового обсл-я, в теорет. физике, астрономии и во многих др. теорет. и прикл. науках. ТВ служит также для обосн-я матем. и прикл. стат-ки, кот. в свою очередь исп. при план-нии и орг-ции пр-ва, при анализе технол. пр-сов и для мн. др. целей.
2. Случайные события, их классификация. Действия над событиями Событие наз-ся СЛУЧАЙНЫМ, если оно может произойти или не произойти в данном опыте. Опыт-осущ.комплекса условий и действий, при котором происх. комплекс явлений. Возможный рез-т опыта-это событие. Виды событий:достоверное (обязательно произойдет в данном опыте); невозможное (не может произойти в данном опыте); случайное.2 события наз-ся совместимыми если появл-е одного из них не искл. появл-е др в данном опыте;2 события несовместимы, если они не могут произойти при одном и том же испытании;2 события противоположны, если появл-е одного из них равносильно появл-ю др.Действия:1)суммой или объединением 2-х событий наз-т соб-е, состоящее в появлении хотя бы одного из них (А+В=АUВ); 2)Произведением или пересечением наз-ся соб-я, состоящие в их одновр. появлении (АВ=АחВ);3) разностью А и В наз-т соб-е, состоящее из исходов входящих в А, но не входящих в В (А-В или В-А)
3. Классическое, статистическое и геометрическое определение вероятности Под вер-тью события понимается некоторая числовая хар-ка возм-ти наступления этого события.
1)статистическое опр-е вер-ти заключается в том,что за вер-тью события А принимается пост.вел-на, вокруг которой колеблются значения частостей при неограниченном возрастании числа n.2)Классической вер-тью события А наз-т отношение числа m элементарных событий, благоприятствующих событию А,к числу n всех элементарных событий из этой схемы: Р(А)=m/n,0≤P(A)≤1. 3)Обобщением клас.схемы явл. пространство событий,элементарные исходы которого можно представить в виде точек,заполняющих некоторую обл Ω в трехмер пространстве R3. Если при этом событию А благоприят-ствуют элементар соб-я,заполняющие некоторую подобласть DизΩ,то геометр вер-тью соб-я А наз-т отношение объема обл D к объему облΩ:Р(А)=V(D)/V(Ω).
4. Элементы комбинаторики: размещения, перестановки и сочетания. 1)множество, состоящее из одних и тех различ. эл-тов и отличающиеся др от др их порядком, называется перестановкой их эл-тов. Число возможных перестановок Рn=n!.2) размещение - мн-во,состоящее из m разл эл-тов по n эл-тов, которые отлич либо составом эл-тов, либо их порядком (Аmn=n(n-1)*…*(n-m+1)). 3)сочетанием из n разл эл-тов по m эл-тов из числа n заданных наз-т мн-во, содержащее m эл-тов, которые отлич хотя бы одним эл-том(Cmn=n!/m!(n-m)!). Св-ва сочетаний:1)С0n=1;2)Cnn=1;3)Cnm=Cn-mn; 4)C0n+C1n+C2n+…+Cnn=2n5)Cmn=Amn/Pm
5.Теорема сложения вероятностей несовместных событий
Т. Вер-сть появл-я 1 из двух несовм. событий, безразлично какого, равна сумме вер-стей этих событий: Р(А + В) = Р А) + Р(В). Док-во: Введем обознач-я: n — общее число возм. элемент. исходов испыт-я; m1 — число исходов, благоприят. событию A; m2— число исходов, благоприят. событию В. Число элемент. исходов, благоприят. наступл-ю либо события А, либо события В, равно m1 + m2. Следовательно, Р (A + В) = (m1 + m2) / n = m1 / n + m2 / n. Приняв во внимание, что m1 / n = Р (А) и m2 / n = Р (В), окончат. получим Р (А + В) = Р (А) + Р (В). Следствие 1. В-сть появления 1 из нескольких попарно несовм. событий, безразлично какого, равна сумме в-стей этих событий:Р (A1 + A2 + ... + An) = Р (A1) + Р (A2) + ... + Р (An). С л е д с т в и е 2: Сумма в-стей противоп. событий равна 1: P(A)+P(A с чертой)=1.
6. Зависимые и независимые события. Условная вероятность. Теорема умножения вероятностей. Вер-сть события В при усл-и, что А уже произошло, наз. условной в-стью события В. Обозн. РА(В) или Р(В/А). РB(А)= =Р(АВ)/Р(В),Р(В)не равно 0.Отсюда следуют Р(АВ)=РВ(А)Р(В), Р(В)>0 и Р(АВ)= РА(В)Р(А),Р(А)>0.Событие А наз. независимым от события В с вер-стью Р(И) не равной 0, если РВ(А)=Р(А),т. е. вер-сть наступления события А не зависит от того, произошло событие В или нет. Теорема умн-я вер-стей. Вер-сть совместного наступл-я 2 событий равна произвед-ю вер-сти одного из них на усл. в-сть другого, вычисленную в предполож-и, что первое событие уже наступило: Р(АВ)=Р(А)РА(В). В частности для независ. событий Р(АВ)=Р(А)Р(В), т. е. в-сть совместного наступл-я 2 независ. событий равна произв-ю вер-стей этих событий.
7. Теорема сложения вероятностей совместных событий. Суммой 2-х совместных событий называют событие, состоящее в появлении либо события A, либо события B, либо обоих сразу.
Теорема. В-сть появл-я хотя бы 1 из 2 совм. событий равна сумме вер-стей этих событий без вер-сти их совм. появл-я: Р(А + В)=Р(А) + Р(В) – Р(АВ). Док-во: Пусть n – число всех элемент. исходов опыта, k – число исходов, благоприятств. событию А, l – число исходов, благоприятств. событию В, m – число исходов, одновременно благопр. А и В. А+В=k+l-m. P(А+В)=(k+l-m)/n=k/n+l/n+m/n=P(A)+P(B)-P(AB). Т-ма м. б. обобщена на любое конечн. число совм.событий: P(A1+A2+A3+…+An)=P(A1)+P(A2)+P(A3)+…+P(An)-P(A1A2)-P(A1A3)-…-P(An-1An)+P(A1A2A3)+…+P(An-2An-1An)-…+(-1)n-1*P(A1A2…An).
8.
Вероятность появления хотя бы одного
из нескольких независимых событий
Пусть
независимые события А1, А2…Аn
имеют одинак. в-сть, равную p.
Тогда Вероятность появления хотя бы
одного из событий А1, А2,…,Аn, независимых
в совокупности, равна разности между
единицей и произведением вероятностей
противоположных событий, т.е.
![]() .
В
частности, если все n событий имеют
одинак. в-сть, равную p, то в-сть появл-я
хотя бы 1 из этих событий равна
P(А)=1-(1-p)n.
.
В
частности, если все n событий имеют
одинак. в-сть, равную p, то в-сть появл-я
хотя бы 1 из этих событий равна
P(А)=1-(1-p)n.
9.
Формула полной вероятности. Формулы
Байеса. Ф-ла
полной вер-ти:
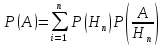 .Док-во:по
условию событие А может произойти с
одним из несовместимых событий Н1,Н2,…Нn,
тогда использ ф-ла алгебры событий
можно записать А=Н1A+Н2A+…+НnА.
Cобытия
Н1А…НnА несовместимые,т.к. Нi,i=1,n-несоверш,
тогда вер-ть событий Р(А)=Р(Н1А)+Р(Н2А)+…+Р(НnА)=
Р(Н1)Р(А/Н1)+…+Р(Нn)Р(А/Нn).что и требовалось
д-ть.Ф-ла Байеса:
.Док-во:по
условию событие А может произойти с
одним из несовместимых событий Н1,Н2,…Нn,
тогда использ ф-ла алгебры событий
можно записать А=Н1A+Н2A+…+НnА.
Cобытия
Н1А…НnА несовместимые,т.к. Нi,i=1,n-несоверш,
тогда вер-ть событий Р(А)=Р(Н1А)+Р(Н2А)+…+Р(НnА)=
Р(Н1)Р(А/Н1)+…+Р(Нn)Р(А/Нn).что и требовалось
д-ть.Ф-ла Байеса: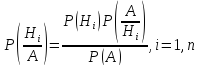 ,где
Р(А) вычисляется по формуле полной
вер-ти. Док-во: В силу усл-я А=Н1А+Н2А+
…+НnA. Найдем вер-ть события Р(НiА).По
теореме умножения вер-ти имеем
Р(НiА)=Р(Нi)P(A/Hi)=P(A)P(Hi/A)
,где
Р(А) вычисляется по формуле полной
вер-ти. Док-во: В силу усл-я А=Н1А+Н2А+
…+НnA. Найдем вер-ть события Р(НiА).По
теореме умножения вер-ти имеем
Р(НiА)=Р(Нi)P(A/Hi)=P(A)P(Hi/A)
P(Hi/A)=P(Hi)P(A/Hi)/P(A).что и треб д-ть.
10. Повторные независимые испытания. Формула Бернулли.
Опыты наз-ся независимыми,если при каждом из них событие А наступает с одной и той же вер-тью Р(А)=р, независящий от того появилась или не появилась в др испытаниях. При этом вер-ть противоположного события Р(Ā)=q,причем p+q=1.
Пусть произ-ся испытание,в каждом из которых может появится событие А или Ā.Вер-ть события А появ-ся в серии из n-независимых испытаний ровно m раз(m≤n)может быть вычислено по формуле Бернулли:
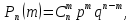
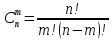
11. Наивероятнейшее число появлений события в схеме Бернулли. Число наступлений m0 события А называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления события А любое другое количество раз. Наивероятнейшее число наступлений события А в n испытаниях заключено между числами np-q и np+p : np-q≤m0≤np+p. Если np-q – целое число, то наивероятнейших чисел 2: np-q и np+p.
12. Локальная и интегральная теоремы Лапласа. Локальная.Если вер-ть наступл-я соб-я А в кажд. из n незав. испыт-й =одной и той же пост величине(n>10), причем p(o<р<1), а n велико, то вер-ть Рn(m) того, что в этих испытаниях соб-е А наступит ровно m раз выч-ся по ф-ле: Pn(m)= (1/√npq)*φ(x), где x=m-np/√npq, φ(x)=(1/√2π)*e-x2/2 ; замечания:φ(-x)=φ(x), для х>5 φ(x)=0. Интегральная.Если вер-ть наступл-я соб-я А в кажд. из n незав-х испыт-й =р, причем o<р<1, а n велико, то вер-ть того, что событие А в этих испыт-х наступит m раз, причем m1<m<m2, м. найти: Рn(m1<m<m2)=(0.5)(Φ(x2)-Φ(x1), где x1=m1-np/√npq, x2=m2-np/√npq, Ф(x) –ф-ция Лапласа=(1/√2π)∫x0℮-t в квадрате/2dt. Применяют если npq>9. Св-ва ф-ции: Ф(x)= -Ф(x), Ф(х) – возраст-т на R, для х>5 Ф(х)=0,5.
13. Формула Пуассона для редких событий. Ф-ла Pn(m)=(1/√npq) φ ((m-np)/√npq) (1)позволяет получать тем более близкие к точному значения Pn(m) результаты, чем больше знач. корня √npq и чем ближе знач . p и q к ½.Если в-сть успеха р по отдельным испытаниям близка к 0 (такие события наз. редкими), то даже при большом n, но малом np (np<10) в-сти, полученные по ф-ле (1) недостаточно близки к их истинным знач. В этом случае прим. другую асимптотическую ф-лу – ф-лу Пуассона. Теорема: Если в-сть наступления события А в каждом из независимых испытаний постоянна, но близка к 0, а np=λ<10, то n(m)≈λm(e-λ/m!) Замечание: ф-лу Пуассона исп., когда n≥10 (n≥100), а np≤10.
14. Дискретная случайная величина, ее закон распределения. Многоугольник распределения. Случ.вел. – переменная вел., к-рая в зав-ти от исхода опыта принимает значения, в зав-ти от случая. ДСВ – случ.вел., приним. разл. значения, к-рые м. записать в виде кон. или беск. посл. чисел. НСВ – случ.вел., к-рая м. принимать все знач-я из нек-рого промежутка. З-н распр. ДСВ – соответствие м-ду знач-ми х1, х2, х3… этой вел. и их вер-тями р1, р2, р3… Если ДСВ Х приним. конечное множ-во знач-й х1, х2…хn с вер-тями р1, р2…рn, то ее з-н распределения опред-ся: Р(Х=хk)=Pk, k=1,n (При этом ΣРk=1). М. задать табличкой:
|
х |
х1 |
х2 |
… |
хn |
|
р |
р1 |
р2 |
… |
рn |
Ряд распр-я ДСВ можно изобразить графически в виде полигона или многоугольника распр-я вер-стей. Для этого по горизонт. оси в выбранном масштабе нужно отложить знач-я СВ, а по вертик. – в-сти этих знач-й, тогда точки с корд-тами (xi , pi ) будут изображать полигон распр-я в-стей. Соединив же эти точки отрезками прямой, получим многоуг-к распр-я в-стей.
15. Функция распределения вероятностей случайной величины и ее свойства. Функцией распределения случайной величины Х называется функция FX(x)= P{X<x}, xR. Под {X<x}понимается событие, состоящее в том, что случайная величина Х принимает значение меньшее, чем число х. Если известно, о какой случайной величине идёт речь, то индекс, обозначающий эту случайную величину, опускается: F(x) FX(x). Как числовая функция от числового аргумента х, функция распределения F(x) произвольной случайной величины Х обладает следующими свойствами:1)для любого xR: 0 F(x) 1. 2) F(-) = limx F(x) = 0 ; F(+) = limx F(x) = 1;3) F(x)-неубывающая функция, т.е.для любых α,βтаких, что α< β :F(β) - F(α);4)непрерывна слева
16.
Математическое ожидание дискретной
случайной величины и его свойства. Мат.
ожидание ДСВ Х, принимающее конечное
множество значений с законом распределения
P(x=xk)=Pk
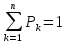 вычисляется по формуле: M(x)=
вычисляется по формуле: M(x)=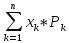 или M(x)=x1P1+x2P2+….+xnPn Математическое
ожидание дискретной случайной величины
≈ среднему арифметическому всех
значений этой случайной величины.
Свойства M(x): 1. a≤M(x)≤b, где a – наименьшее,
b – наибольшее значение случайной
величины X. 2. M(C)=C,
где
C=const. 3. M(Cx)=C*M(x) 4. M(X≠Y)=M(X)≠M(Y) 5. M(xy)=M(x)*M(y)
или M(x)=x1P1+x2P2+….+xnPn Математическое
ожидание дискретной случайной величины
≈ среднему арифметическому всех
значений этой случайной величины.
Свойства M(x): 1. a≤M(x)≤b, где a – наименьшее,
b – наибольшее значение случайной
величины X. 2. M(C)=C,
где
C=const. 3. M(Cx)=C*M(x) 4. M(X≠Y)=M(X)≠M(Y) 5. M(xy)=M(x)*M(y)
17. Дисперсия дискретной случайной величины и ее свойства. Среднее квадратическое отклонение. На практике часто требуется оценить рассеяние возм. знач-й случ. вел-ны вокруг ее среднего значения. Дисперсией (рассеиванием) лучайной величины X называется математическое ожидание квадрата ее отклонения от ее мат. ожидания, т.е. D(X)=M(X-M(X))2 или D(X)=M(X2)-(M(X))2 Свойства: 1. D(X)≥0 2. D(C)=0 3. D(CX)=C2D(X) 4. D(X±Y)=D(X)±D(Y) Ср.квадратич. отклонением СВ Х наз-ся величина σ (Х)= корень квадр. из D(X)
Среднее квадр. откл-е характ. степень откл-я СВ от ее мат. ожид-я и имеет размерность знач-й СВ.
18.
Биномиальный закон распределения и
его числовые характеристики.
Пусть проводится n независимых испытаний.
В результате каждого из которых возможны
2 исхода: А – успех с вероятностью p, или
 -
неуспех с вероятностью q = 1-p. Тогда
вероятность числа m успех
-
неуспех с вероятностью q = 1-p. Тогда
вероятность числа m успех
 Дискретная
случайная величина X, которая может
принимать только целые неотрицательные
значения с вероятностями P (X=m)=
Дискретная
случайная величина X, которая может
принимать только целые неотрицательные
значения с вероятностями P (X=m)= , где p>0, q>0,
m
, где p>0, q>0,
m
 0,n
называется распределенной по
биноминальному закону с параметром p.
Мат.ожидание M(X)= np Дисперсия
0,n
называется распределенной по
биноминальному закону с параметром p.
Мат.ожидание M(X)= np Дисперсия

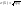 -
среднее квадратическое отклонение.
-
среднее квадратическое отклонение.
19. Геометрическое распределение. Геометрическим распределением называется распределение ДСВ X, определяемое формулой P(X=m)=(1-p)m-1*p, 0<p<1, m=1, 2, 3…
Вероятности
образуют бесконечно убывающую
геометрическую прогрессию со знаменателем
q=1-p (с этим связано название). Мат.
ожидание равно M(x)=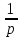 Дисперсия равна D(x)=
Дисперсия равна D(x)=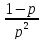
20.
Гипергеометрическое распределение.
Пусть
имеется N
элементов, из кот-х М эл-тов облад.
некот-м признаком А. извлек. случ. образом
без возвращ-я n
эл-тов. X
– ДСВ, число эл-тов, облад. признаком
А, среди отобр. n
эл-тов. В-сть, что Х =m
опред. по формуле: P(x=m)=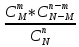 Мат. ожидание и дисперсия СВ, распред.
по гипергеом. закону, опред. формулами:
M(x)=n*
Мат. ожидание и дисперсия СВ, распред.
по гипергеом. закону, опред. формулами:
M(x)=n*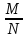 ,
D(x)=n
,
D(x)=n
21.
Формула Пуассона. Распределение
Пуассона. Если
число испытаний велико, а вер-сть появл-я
события в каждом испытании очень мала,
то используют приближенную формулу
Пуассона: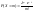 ,где
λ=np (среднее число появл-я события в n
испытаниях), m – число появления события
в n независимых испытаниях; m приним.
значения 0,1,2,…,n. Мат. ожидание и дисперсия
СВ, распределенной по закону Пуассона,
совпадают и равны параметру λ : M(X)=λ,
D(X)=λ, Т.к. для распред. Пуассона вер-ть
появления события в каждом испытании
мала, то его еще назыв. з-н распред.
редких явлений.
,где
λ=np (среднее число появл-я события в n
испытаниях), m – число появления события
в n независимых испытаниях; m приним.
значения 0,1,2,…,n. Мат. ожидание и дисперсия
СВ, распределенной по закону Пуассона,
совпадают и равны параметру λ : M(X)=λ,
D(X)=λ, Т.к. для распред. Пуассона вер-ть
появления события в каждом испытании
мала, то его еще назыв. з-н распред.
редких явлений.
22.
Непрерывная случайная величина,
плотность распределения вероятностей
непрерывной случайной величины и ее
свойства. Случ.
вел-на Х наз. непрерывной, если ее функция
распред-я непрерывна в любой точке и
дифференцируема всюду, кроме отдельных
точек. Теорема. Вероятность любого
отдельного знач-я непрер. случ. вел-ны
равна нулю: P(X=x1)=0.
Для НСВ P(x1<
X
< x2)=F(x2)-F(x1).
Ф-ция
распред.опис.как ДСВ, так и
непрерыв.СВ,однако,такой способ задания
неперыв.СВ не единств.Их удобно описывать
ф-цией,кот. наз. плотностью распред.вероят.или
дифференц.ф-цией.(Р(Х)-дифференц.ф-ция
плотность интегральная). Плотностью
распред. вероят.непрерыв. СВ X наз. ф-ция
р(х),кот. равна первой производной от
ф-ции распред.Р(Х),т.е р(х)=F’(х).
Свойства: 1.(вместо f
– p)
1.f(x)≥0 для люб.x – cв-во неотриц-ти.2.
 3.
3.
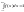 -
Cв-во нормировки.
-
Cв-во нормировки.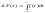
23.
Математическое ожидание и дисперсия
непрерывной случайной величины
Мат.ожид.НСВ Х, все знач., кот. х
принадлежит[альфа,бета] с плотностью
вероят.р(х), вычисл. по формуле:
![]() Если
НСВ X определена на(-00;+°°),то мат.ожид.
опред. по формуле
Если
НСВ X определена на(-00;+°°),то мат.ожид.
опред. по формуле
![]() (требуется
абсолют.сходимость интеграла.)
(требуется
абсолют.сходимость интеграла.)
Дисперсия
НСВ, X принадлежит интервалу (альфа,
бета) с плотностью р(Х) вычисл.по
формуле:
![]() (абсолют.сходимость
интеграла требуется)
(абсолют.сходимость
интеграла требуется)
![]()
![]()
24. Равномерный закон распределения и его числовые характеристики Непр. случ. велич.х распред. равномерно на отрезке [а;b], если её плотность вероятности р(х) постоянна на этом отрезке и =0 вне его:
Р(х)= {1/ (b-a), при а< =х<=b, О, при х<а, х>b
Функция распред. случайн. величины, распред-ой по равномерн. закону, имеет вид:
F(x)= { O, x<=a, (x-a)/(b-a), a<x<=b, 1, x>b
Мат. ожидание, дисперсия, средн. кв. откл-е:МХ=(а+b)/2; DХ=(b-а)( b-a)/ 12
25.
Показательный закон распределения и
его числовые характеристики. Непрерывная
СВ Х имеет показ. (экспоненциальное)
распределение с параметром λ >0, если
ее плотность распред-я имеет вид:
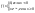
Ф-ция
распределения СВ, распределенной по
показ. з-ну:
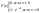
Показательному распределению обычно подчиняется величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств, другими словами – величина промежутка времени между появлениями двух послед-х редких событий. Вероятность попадания случайной величины Х на интервал (α;β)
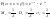
26.
Нормальный закон распределения. Влияние
параметров распределения на вид
нормальной кривой.
Непрерывная
случайная величина X имеет нормальный
закон распределения с параметрами а и ![]() ,
если её плотность вероятности f(x) имеет
вид:
,
если её плотность вероятности f(x) имеет
вид:
![]() Кривая
нормального распределения f(x) (нормальная
кривая или кривая Гаусса) приведена на
рисунке.
Кривая
нормального распределения f(x) (нормальная
кривая или кривая Гаусса) приведена на
рисунке.
![]() График
симметр. относит. а. При изменении
параметра а форма кривой не меняется,
а ее график сдвигается влево или вправо.
При изменении параметра σ меняется
форма нормальной кривой: с увеличением
параметра σ кривая должна приближаться
к 0Х и растягиваться вдоль этой оси, а
с уменьшением σ кривая стягивается к
прямой х=а.
График
симметр. относит. а. При изменении
параметра а форма кривой не меняется,
а ее график сдвигается влево или вправо.
При изменении параметра σ меняется
форма нормальной кривой: с увеличением
параметра σ кривая должна приближаться
к 0Х и растягиваться вдоль этой оси, а
с уменьшением σ кривая стягивается к
прямой х=а.
27.
Числовые характеристики случайной
величины, имеющей нормальное распределение.
Непрерывная
случайная величина X имеет нормальный
закон распределения с параметрами а и ![]() ,
если её плотность вероятности f(x) имеет
вид:
,
если её плотность вероятности f(x) имеет
вид:
![]() Математическое
ожидание случайной величины X,
распределённой по нормальному закону,
равно параметру а этого закона,
а её дисперсия - квадрату параметра
Математическое
ожидание случайной величины X,
распределённой по нормальному закону,
равно параметру а этого закона,
а её дисперсия - квадрату параметра ![]() ,
т.е.
,
т.е.
![]() Величина М(Х)
называется также центром рассеяния, а
среднеквадратичное отклонение
Величина М(Х)
называется также центром рассеяния, а
среднеквадратичное отклонение
![]() характеризует
ширину кривой распределения. С
возрастанием
характеризует
ширину кривой распределения. С
возрастанием
![]() максимальная ордината кривой убывает,
а сама кривая становится более пологой,
растягиваясь вдоль оси абсцисс, тогда
как при уменьшении
максимальная ордината кривой убывает,
а сама кривая становится более пологой,
растягиваясь вдоль оси абсцисс, тогда
как при уменьшении
![]() кривая
вытягивается вверх, одновременно
сжимаясь с боков
кривая
вытягивается вверх, одновременно
сжимаясь с боков
28.
В-сть попад-я в зад. интервал нормально
распред. случ. в-ны. В-сть зад. откл-я.
Правило трех сигм. В-сть
попадания нормально распр. СВ Х в
заданный интервал ![]() опр.
ф-лой
опр.
ф-лой![]() .Часто
требуется вычислить вероятность того,
что отклонение нормально распределенной
случайной
величины Х
от ее М(х) =а по абсол. величине меньше
заданного полож. числа ε.
.Часто
требуется вычислить вероятность того,
что отклонение нормально распределенной
случайной
величины Х
от ее М(х) =а по абсол. величине меньше
заданного полож. числа ε.
![]() ;
;![]() ;
;![]() При
реш-и многих важных практич. задач
делают предпол-е, что СВ распределена
по норм. закону. Возн. вопрос, на каком
основании делается такое допущение.
Для иссл-я этого вопроса рассм. одну
характ. особ-сть норм. распред-я СВ.
Найдем в-сти событий: |x-a|<σ ;|x-a|<2σ ;
|x-a|<3σ Используем формулу:P(|x-a|<σ)=2Ф(1)=0,6826
P(|x-a|<2σ)=2Ф(2)= 0,9594 P(|x-a|<3σ)=2Ф(3)=0,9973 – это
событие практически достоверное.Заглянем
в таблицу: Из последнего соотношения
следует, что практически все возможные
значения норм. распр-я СВ x принадлежат
интервалу (a-3σ; a+3σ)
При
реш-и многих важных практич. задач
делают предпол-е, что СВ распределена
по норм. закону. Возн. вопрос, на каком
основании делается такое допущение.
Для иссл-я этого вопроса рассм. одну
характ. особ-сть норм. распред-я СВ.
Найдем в-сти событий: |x-a|<σ ;|x-a|<2σ ;
|x-a|<3σ Используем формулу:P(|x-a|<σ)=2Ф(1)=0,6826
P(|x-a|<2σ)=2Ф(2)= 0,9594 P(|x-a|<3σ)=2Ф(3)=0,9973 – это
событие практически достоверное.Заглянем
в таблицу: Из последнего соотношения
следует, что практически все возможные
значения норм. распр-я СВ x принадлежат
интервалу (a-3σ; a+3σ)
29. Моменты случайной величины. Асимметрия. Эксцесс. Начальным моментом ν к СВ X называется математическое ожидание ее k-й степени, т.е. νк=M(xк).Для ДСВ Х, принимает значение X1, X2, …,Xn с вероятностью P1, P2, …Pn.
νk=
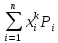 Для НСВ Х с p(x) начальный момент k-о
порядка определяются по формуле:
Для НСВ Х с p(x) начальный момент k-о
порядка определяются по формуле:
νk=M(xn)=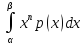 ;
νk=M(xn)=
;
νk=M(xn)=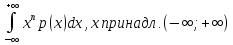
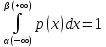 -
условие
-
условие
Центр.
теорет. момент порядка k
х μк=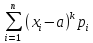
Для
непрер. СВ Х: μк=
Следствия:
1. ν0=1, μ0=1 2. ν1=M(x), μ1=0 3. ν2=M(x2),
μ2=D(x), μ2= ν2-ν12
4.
μ3=v3-3v1v2+2v13.
Ассиметрией теоретического распред-я
наз-ся отн-е центр. момента 3-го пор-ка
к кубу ср. квадр. ожидания. A=
μ3/![]() в
кубе. А=0, если распред-е симметрично
относ-но мат. ожидания.
Для
оценки крутости теоретич. расп-я
примен-ся эксцесс, кот. опр-ся так
в
кубе. А=0, если распред-е симметрично
относ-но мат. ожидания.
Для
оценки крутости теоретич. расп-я
примен-ся эксцесс, кот. опр-ся так
![]()
30. Неравенство Маркова. Если СВ Х принимает неотрицательные значения, т.е. (х≥0, хi≥0) и существует ее мат. ожидание M(x)=a, то для А числа ε>0 выполняется неравенства:
P(x≥ε)<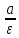 или P(x<ε)≥1-
или P(x<ε)≥1-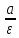 .
Событие x<ε,
x≥ε
след. сумма вероятностей этих событий
=1. P(x<ε)+P(x≥ε)=1
.
Событие x<ε,
x≥ε
след. сумма вероятностей этих событий
=1. P(x<ε)+P(x≥ε)=1
31. Неравенство Чебышева. Если Х-СВ, мат. ожидание к-рой М(Х) = а, а дисперсия D(Х) конечна, то д/любого числа ε > 0 выполняются неравенства:
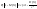
При неизв-ом з-не распред-я на практике при известных М(Х),D(X) участком возможных значений СВ Х считают М(Х)±3σ(Х)
32. Теорема Чебышева. Если СВ-ы Х1, Х2….Хn независимы и имеют мат. ожид. M(x1), M(x2)….M(xn) и дисперсии D(x1), D(x2)…..D(xn), кот. Ограничены одним и тем же числом С, то для А δ>0, вып. неравенство:
P(|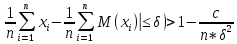
Следствие:
-
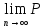 (|
(|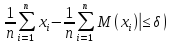 =1
=1 -
Если все СВ Хi имеют одно и тоже мат. ожидание M(xi)=a, i=1,n, то неравенство примет вид:
P(|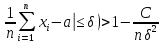
Отсюда следует, что среднее арифметическое при большом n как угодно мало отличается от постоянной величины a.
33.
Теорема Бернулли. Значение закона
больших чисел. Если
вероятность наступления события А в
каж-м из n повторных независимых испытаний
постоянна, то при неограниченном
увеличении числа n исп-й отн-я частота
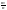 наст-я соб-я А стрем-ся по вер-ти к числу
p, т.е. для
наст-я соб-я А стрем-ся по вер-ти к числу
p, т.е. для

 >0
>0
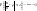 Т-ма
Б-ли явл-ся теор-ким обосн-ем для стат-го
опр-я вер-ти.
Т-ма
Б-ли явл-ся теор-ким обосн-ем для стат-го
опр-я вер-ти.
Неравенство
Бернулли:Пусть
 n
исп-й Бернулли с вер-ю успеха p, q=1-p и m –
число успехов. Тогда для
n
исп-й Бернулли с вер-ю успеха p, q=1-p и m –
число успехов. Тогда для

 >0
>0
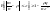
34.
Понятие о центральной предельной
теореме.
Суть центральной предельной теоремы
(ЦПТ) в след.: Если СВ х представляет
собой сумму оч. большого числа взаимно
независимых случ. в-н, влияние каждой
из которых на всю сумму ничтожно мало,
то х имеет расп-е, близкое к нормальному.
Центральная предельная теорема (ЦПТ)
( в формулировке Ляпунова А.М. для
одинаково распред. СВ). Если попарно
независимые СВ X1, X2, ..., Xn, ... имеют
одинаковый закон распределения с
конечными числовыми характеристиками
M[Xi] =
и D[Xi] = 2,
то при n
закон распределения СВ
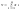 неограниченно приближается к норм.
закону N(n,
неограниченно приближается к норм.
закону N(n,
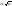 ).
Следствие. Если в условии теоремы СВ
).
Следствие. Если в условии теоремы СВ
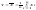 ,
то при n
закон распределения СВ Y неограниченно
приближается к нормальному закону N(,
/
,
то при n
закон распределения СВ Y неограниченно
приближается к нормальному закону N(,
/ ).
).
35. Предмет и метод мат. статистики. МС – раздел мат-ки, изуч. методы сбора, систематизации и обработки рез-тов набл-й с целью выявления стат. зак-стей. Оперирует непосредственно с р-тами наблюдений над случ. явлением. Предметом МС явл. изуч-е случ. событий и случ. величин по р-там наблюд-й. Задачи МС: 1.указать способы сбора и группировки стат. сведений, получ. в р-те наблюдений или в р-те спец. поставл. экспер-тов; 2.разработать методы анализа стат. данных в зав-сти от целей иссл-я. Осн. задача МС сост. в получ-и выводов о массов. явлениях по данных наблюдения за ними. МС опирается на ТВ. Ее цель-оценить характер-ки генер. совок-ти по выборочным данным. Стат. совок-сть – совок-сть предметов или явл-й объед. каким-л. общим признаком. Р-том наблюд-й над ста. совок-стью явл. стат. данные. Обработка стат. данных методами МС приводит к установл-ю опред. законом-стей, присущих массовым явл-ям.
