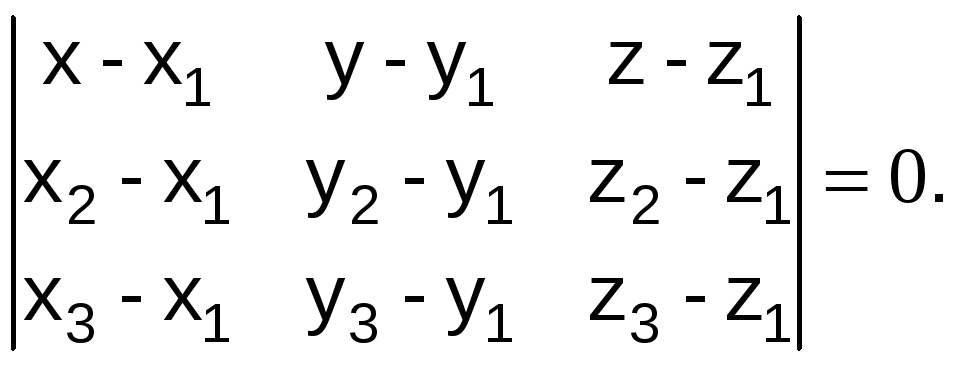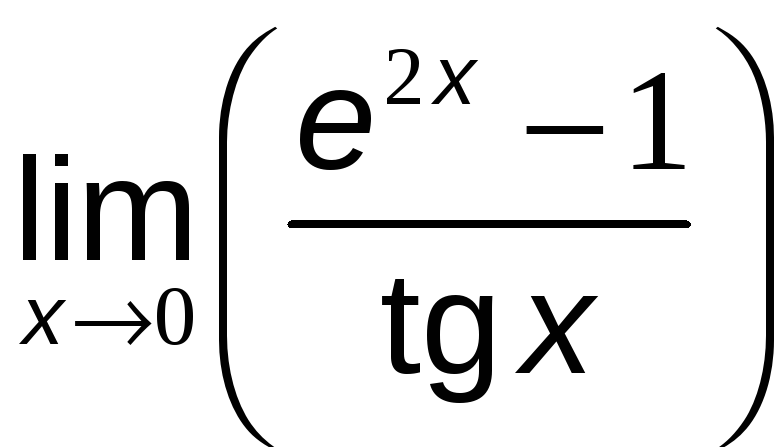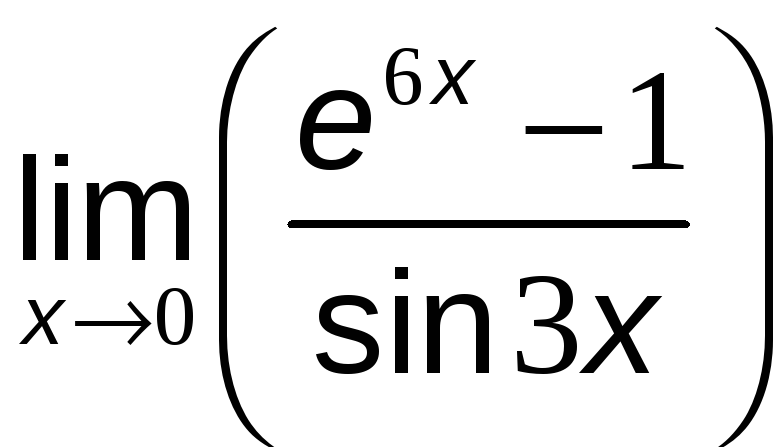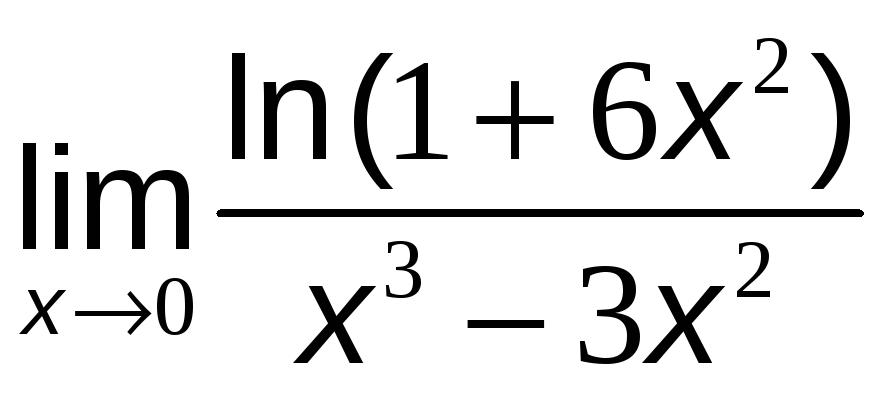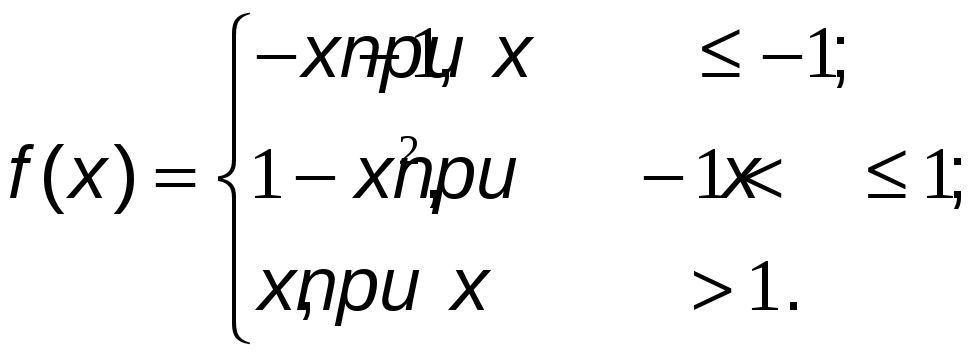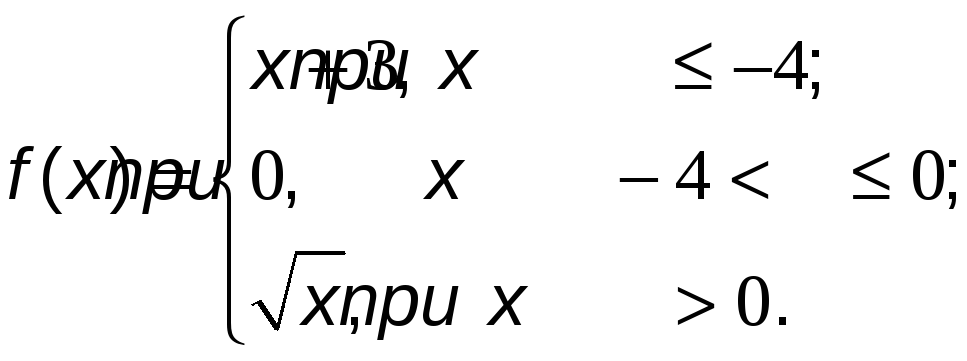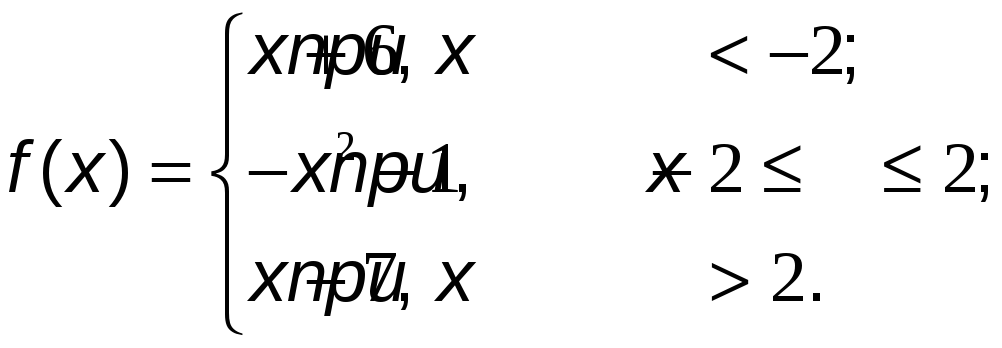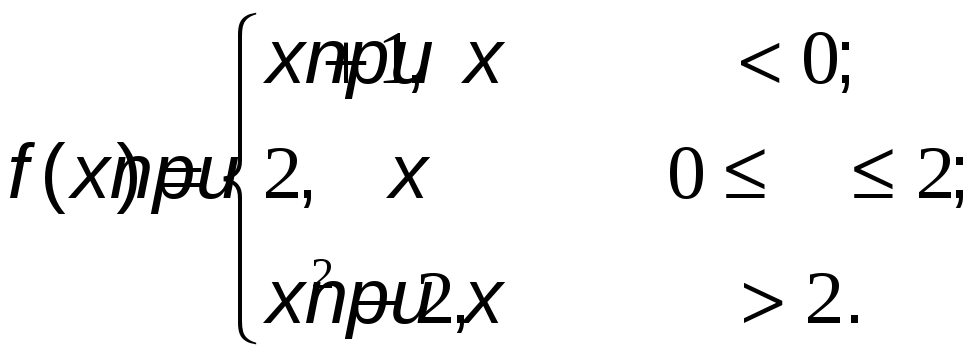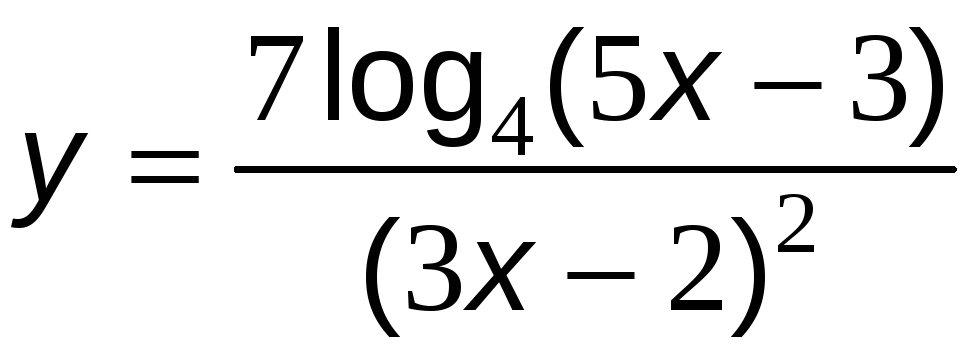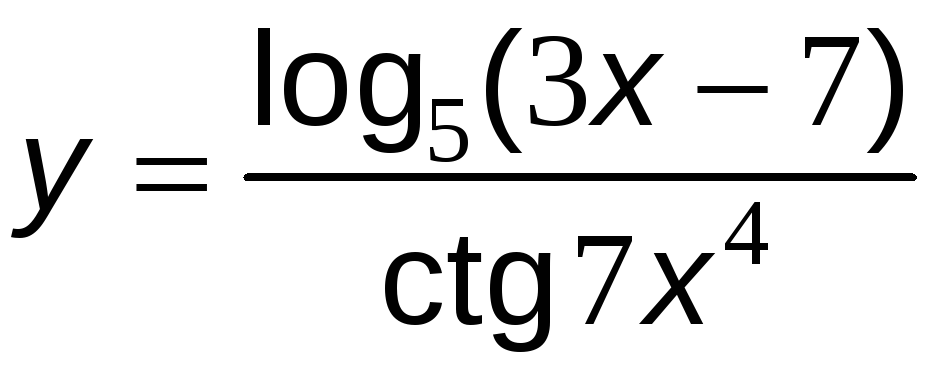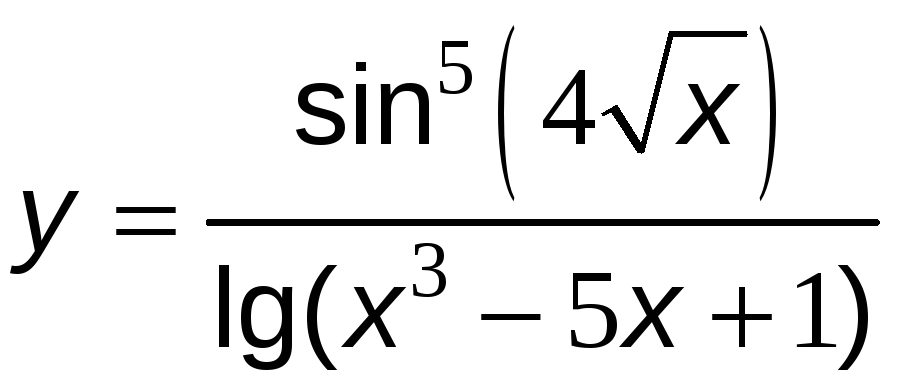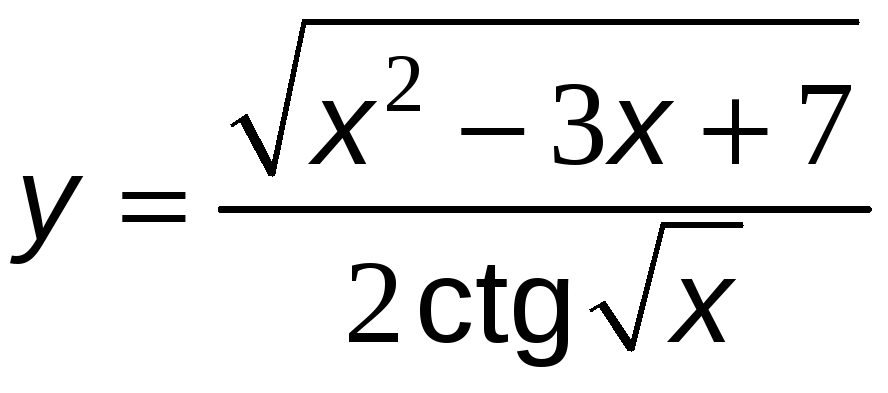Аттестация 1 семестр

№11 Вычислить предел, используя эквивалентные бесконечно малые функции

1		2
3		4
5		6
7		8
9		10
11		12
13		14
15		16
17		18
19		20
21		22
23		24
25		26
27		28
29		30

№12 Исследовать функцию на непрерывность и построить ее график.

1.		6.
2.		7.
3.		8.
4.		9.
5.		10.
11		12
13		14
15		16
17		18
19		20
21		22
23		24
25		26
27		28
29		30

№13 Найти производные функций.

1	а) б) в)	2	а) б) в)
3	а) б) в)	4	а) б) в)
5	а) б) в)	6	а) б) в)
7	а) б) в)	8	а) б) в)
9	а) б) в)	10	а) б) в)
11	а) б) в)	12	а) б) в)
13	а) б) в)	14	а) б) в)
15	а) б) в)	16	а) б) в)
17	а) б) в)	18	а) б) в)
19	а) б) в)	20	а) б) в)
21	а) б) в)	22	а) б) в)
23	а) б) в)	24	а) б) в)
25	а) б) в)	26	а) б) в)
27	а) б) в)	28	а) б) в)
29	а) б) в)	30	а) б) в)

№14 Найти предел используя правило Лопиталя.

1.		6.
2.		7.
3.		8.
4.		9.
5.		10.
11		12
13		14
15		16
17		18
19		20
21		22
23		24
25		26
27		28
29		30

№15 Найти промежутки возрастания и убывания, точки максимума и минимума функции, промежутки вогнутости и выпуклости, точки перегиба графика функции:

1.		6.
2.		7.
3.		8.
4.		9.
5.		10.
11		12
13		14
15		16
17		18
19		20
21		22
23		24
25		26
27		28
29		30

Рекомендации к решению:

№6. Даны векторы . Вычислить .

Решение:

.

.

Ответ: 31.

№7. Найти угловой коэффициент прямой, проходящей через точки и .

Решение:

Составим уравнение прямой AB, как уравнение прямой проходящей через две точки:

.

Выражаем : . Угловым коэффициентом является коэффициент при : .

Ответ: .

№8. Даны координаты вершин треугольника . Найти площадь треугольника .

Решение:

Площадь треугольника АВС равна , где – сторона треугольника, – его высота.

Найдём длину стороны AB: .

Составим уравнение прямой AB, как уравнение прямой проходящей через две точки:

.

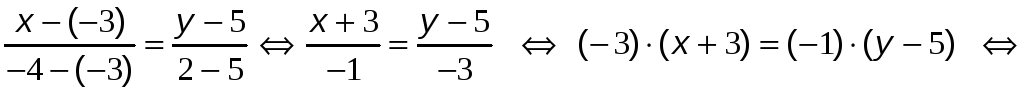
Найдём длину высоты СН как расстояние от точки С до прямой АВ:

Окончательно получаем:

Ответ: 12.

№9. Найти расстояние от точки до плоскости, проходящей через точки , и :

Решение:

Уравнение плоскости, проходящей через три точки, имеет вид: