2.3. Декодер Меггита для укороченных бчх-кодов

Для декодирования укороченных БЧХ-кодов при построении декодера Меггита с предварительным умножением на x^k необходимо построить дополнительный полином d(x), который рассчитывается следующим образом:

d(x) = x^i+k mod g(x), (2.7)

где i – количество символов, на которые был укорочен код.

И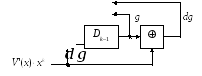зменения в структуре декодера Меггита можно рассмотреть на следующей схеме (рис. 2.4).

Рис. 2.4. Пояснения к дополнению структуры декодера Меггита

На рис. 2.4 D_k–1 – последний элемент памяти генератора синдрома. Обозначение «dg» означает, что обратная связь с выхода сумматора заводится на элементы памяти с номерами, совпадающими с показателями степеней слагаемых, которые входят и в порождающий полином g(x), и в дополнительный полином d(x). Обозначение «» означает, что обратная связь с выхода элемента памяти D_k–1 заводится на элементы памяти с номерами, совпадающими с показателями степеней слагаемых, которые входят в порождающий полином g(x) и при этом не входят в дополнительный полином d(x). Обозначение «» означает, что прямая связь с входа заводится на элементы памяти с номерами, совпадающими с показателями степеней слагаемых, которые входят в дополнительный полином d(x) и при этом не входят в порождающий полином g(x).

Из анализа вида дополнительного полинома d(x) можно сделать вывод о том, что для неукороченного кода дополнительные связи в декодере отсутствуют. Действительно, полином d(x) определяется следующим образом:

d(x) = x^i+k mod g(x) = | _{i = 0} = x^k mod g(x).

Значит, полином d(x) содержит все слагаемые полинома g(x), за исключением слагаемого x^k. Поэтому связь «dg» с выхода последнего сумматора заводится по полиному g(x), связь «» содержит один компонент x^k и является вырожденной (отсутствует), связь «» не содержит ни одного компонента и также является вырожденной (отсутствует).

Пример 2.4. Для укороченного циклического кода (5,2,3) и проверочного полинома g(x) = 1  x²  x³ построить декодер Меггита с предварительным умножением на x^k.

Код (5,2,3) построен от табличного кода (7,3,4) путем укорочения информационной части на i = 2. Построим дополнительный полином d(x):

d(x)=x^i+k mod g(x)= x²⁺³ mod (1  x²  x³) = 1  x.

Определим сочетания для введенных обозначений.

dg (слагаемые есть и в g(x), и в d(x)): 1;

(слагаемые есть в g(x), но нет в d(x)): x², x³;

(слагаемые есть в d(x), но нет в g(x)): x.

Настройка селектора определяется как x^k–1= x³.

С учетом дополнительных связей построим декодер Меггита для укороченного кода с предварительным умножением на x^k (с универсальной настройкой селектора) (рис. 2.5).

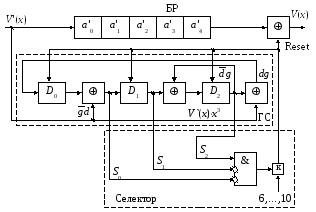
Рис. 2.5. Декодер Меггита для укороченного кода (5,2,3)

Запишем функции возбуждения для элементов памяти:

Промоделируем работу декодирующего устройства для полинома V(x) = 1  x²  x³ при однократной ошибке в разряде a₃ (полином ошибки e(x) = x³). Результаты моделирования сведем в табл. 2.6.

Таблица 2.6

e(x) = x3
№ такта	e	D0	D1	D2
		0	0	0
1	0	0	0	0
2	1	1	1	0
3	0	0	1	1
4	0	1	0	0
5	0	0	1	0
6	0	0	0	1
7	0	0	0	0

В рассматриваемом случае полином V'(x) будет выглядеть так: V'(x) = V(x)  e(x) = 1  x²  x³  x³ = 1  x².

Согласно предварительным расчетам селектор сработает (ошибочный разряд a₃ попадает в старший разряд буферного регистра) на такте с номером: 25 – 3 – 1 = 6. Исправление произойдет на следующем такте, т. е. на такте с номером 25 – 3 = 7. На этом такте произойдет обнуление элементов памяти генератора синдрома.

Алгоритмы синдромного декодирования укороченных БЧХ-кодов в каналах с независимыми ошибками при исправлении и обнаружении ошибок произвольной кратности аналогичны рассмотренным в предыдущих разделах.

Действительно, для обнаружения ошибок необходимо только вычислить синдром и проверить его на неравенство нулю. В этом случае нет необходимости в вычислении дополнительного полинома d(x), поскольку обнаружение ошибки (стирание сообщения) происходит на (n + 1)-м такте работы декодирующего устройства. Напомним, что дополнительный полином d(x) строится для обеспечения свойства замкнутости укороченного (псевдоциклического) БЧХ-кода относительно операции циклического сдвига, а это необходимо только для исправления ошибок.

Для исправления и обнаружения ошибок укороченными БЧХ-кодами используется либо частный (для кодов Хэмминга), либо общий подход к построению декодирующих устройств. Вне зависимости от применяемого подхода, в подсистеме, реализующей исправление ошибок, необходимо учитывать настройки дополнительного полинома d(x). Все остальное (элементы, настройки, алгоритмы работы) соответствуют декодирующим устройствам неукороченных кодов, подробно рассмотренных ранее.