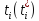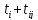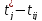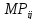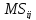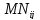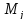Лабораторная работа № 5
Вариант №9
Студента ИТ 14-1 Красовского Абхая
Сетевая модель проекта
Цель работы – Научиться определять критический путь(пути) в сетевой модели проекта, заданного нагруженным ориентированным графом без контуров типа I «событие– операция». Определение резервов операций и событий. Качественный анализ проекта.
Задание
1 Изучить основные понятия для исследования сетевой модели проекта типа I «событие– операция».
2 Изучить структуру событий (вершин сети) и их временную привязку к началу выполнения проекта.

Методические указания
1 Изучить теоретический материал к лабораторной работе.
2 При необходимости, преобразовать сетевую модель проекта к стандартному виду (по одной вершине только с исходящими (начало проекта) и только входящими (окончание проекта) ребрами).
3 При выполнении п. 3 расписать процедуру получения вершинами временных отметок для 3-х вершин (для остальных – выполнить устно).
4 Для 2-х любых соседних вершин представить графически структуру событий с привязкой ко времени начала проекта и различных резервов времени
t = ] N / 9 [ = ] 9 / [ = 0.
Решение
Определим время выполнения проекта и критического пути от начала до конца
1.Найдем вершину в сети, не имеющую входящих дуг и поставим ей отметку 0. В нашем случае это вершина S.
2.Перейдем от вершины с отметкой к смежной с ней вершине и вычислим для нее отметку по формуле:
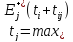
Таким образом вычислим отметку для всех вершин.
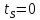
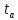 = max { 12 (из вершины S)
} =
= max { 12 (из вершины S)
} =
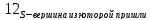
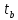 = max { 12 + 8 (из в.
a ); 0 + 21 (из в.
S) } =
= max { 12 + 8 (из в.
a ); 0 + 21 (из в.
S) } =

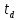 = max { 12 + 14 (из в. a);
21 + 7 (из в. b) } =
= max { 12 + 14 (из в. a);
21 + 7 (из в. b) } =
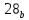
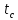 = max { 28 + 12 (из в. d);
21 + 17 (из в. b) } =
= max { 28 + 12 (из в. d);
21 + 17 (из в. b) } =
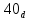
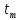 = max { 28 + 15 (из в. d)
} =
= max { 28 + 15 (из в. d)
} =

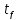 = max { 42 + 9 (из в. m);
21 + 10 (из в. b) } =
= max { 42 + 9 (из в. m);
21 + 10 (из в. b) } =
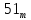
 = max { 51 + 11 (из в. f);
42 + 10 (из в. m) } =
= max { 51 + 11 (из в. f);
42 + 10 (из в. m) } =


Время
выполнения проекта 62 единицы ( = 62)
= 62)
3.Критический
путь
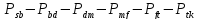
4.Для вершин
не лежащих на критическом пути, определим
 - момент времени для вершин i
не позже которого должна быть начата
работа из множества работ, которые
начинаются в этой вершине с самым
маленьким запасом времени на выполнение
- момент времени для вершин i
не позже которого должна быть начата
работа из множества работ, которые
начинаются в этой вершине с самым
маленьким запасом времени на выполнение
по формуле
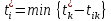
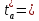 min { 28 – 14 (d);
21 – 8 (b) } =
min { 28 – 14 (d);
21 – 8 (b) } =
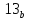
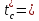 min { 62 – 0 (k)
} =
min { 62 – 0 (k)
} =
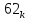
Выполним расчеты резервов различного вида для событий и операций
|
|
|
|
Сроки выполнения работ |
Резервы времени |
|||||||||
|
Работа |
Кол. пред. работ |
Продолж. работ
|
Ранние |
Поздние |
Работ |
Событий |
|||||||
|
н
|
ок
|
н
|
ок
|
|
|
|
|
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|||
|
(Sa) |
0 |
12 |
0(0) |
12 |
1 |
13(12) |
1 |
0 |
1 |
1 |
|||
|
(ab) |
1 |
8 |
12(13) |
20 |
13 |
21(21) |
1 |
1 |
0 |
0 |
|||
|
(ad) |
1 |
14 |
12(13) |
26 |
14 |
28(28) |
2 |
2 |
1 |
0 |
|||
|
(bc) |
2 |
17 |
21(21) |
38 |
45 |
62(40) |
24 |
2 |
24 |
0 |
|||
|
(dc) |
2 |
12 |
28(28) |
40 |
50 |
62(40) |
22 |
0 |
22 |
0 |
|||
|
(bf) |
2 |
10 |
21(21) |
31 |
41 |
51(51) |
20 |
20 |
20 |
0 |
|||
|
(mt) |
1 |
10 |
42(42) |
52 |
52 |
62(62) |
10 |
10 |
10 |
0 |
|||
|
(ck) |
2 |
0 |
40(62) |
40 |
62 |
62(62) |
22 |
22 |
0 |
0 |
|||
Столбец 1
– работы

Столбец 2
- Количество пред. работ =
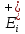 - количество входящих работ
- количество входящих работ
Столбец 3 - Продолжительность работ tij
Столбец 4
=
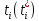 = отметка времени вершины i(момент
времени вершины i)
= отметка времени вершины i(момент
времени вершины i)
Столбец 5
=
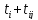 = столбец 4 + столбец 3
= столбец 4 + столбец 3
Столбец 6
=
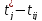 = столбец 7 – столбец 3
= столбец 7 – столбец 3
Столбец 7-
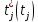 - отметка времени вершины j(момент
времени вершины j)
- отметка времени вершины j(момент
времени вершины j)
Столбец 8
-
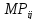 - полный разрыв времени для выполнения
работ =
- полный разрыв времени для выполнения
работ =
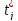 -
-
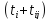 =
столбец 7 – столбец 5
=
столбец 7 – столбец 5
Столбец 9
-
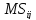 – свободный резерв времени для выполнения
работ =
– свободный резерв времени для выполнения
работ =
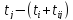 = столбец 7 ()– столбец 5
= столбец 7 ()– столбец 5
Столбец 10
-
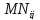 - независимый резерв времени для
выполнения работ =
- независимый резерв времени для
выполнения работ =
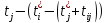 = столбец 7 – (столбец 4() + столбец 3)
= столбец 7 – (столбец 4() + столбец 3)
Столбец
11 -
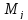 - резерв времени события =
- резерв времени события =
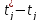 = столбец 7 – столбец 7()
= столбец 7 – столбец 7()