отчёт_lab2

_{МИНОБРНАУКИ РОССИИ}

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра высшей математики №2

отчет

по лабораторной работе №2

по дисциплине «Статистика случайных процессов»

Тема: Прогнозирование

Студент гр. 3381		Сучков А.И.
Преподаватель		Егоров В.А.

Санкт-Петербург

2018

Цель работы.

Научится решать задачи экстраполяции стационарных случайных процессов с дискретным временем.

Основные теоретические положения.

Пусть X_n – стационарный нормальный случайный процесс с дискретным временем имеет нулевое математическое ожидание и ковариационную функцию K(n). Задача экстраполяции состоит в выборе оценки 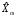значения процесса X_n, зависящей только от значений процесса 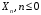, таким образом, чтобы минимизировать .

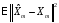Теоретически задача экстраполяции процесса решается формулой 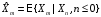, 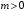где справа стоит условное математическое ожидание. Цель задачи экстраполяции заключается в том, чтобы свести нахождение функции прогноза 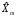к простым и быстрым вычислениям.

В общем случае обычно находят оптимальную линейную оценку, для чего достаточно решить задачу для нормального процесса с ковариационной функцией K(n). Полученная линейная оценка окажется оптимальной линейной оценкой для исходной задачи.

Постановка задачи.

Задание №1: Пусть спектральная плотность стационарного случайного процесса равна 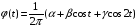. Построить функции оптимального линейного прогноза.

Задание №2: Пусть спектральная плотность стационарного случайного процесса равна 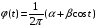. Найти ковариационную функцию и построить функции оптимального линейного прогноза. Представить процесс в виде скользящего среднего.

Задание №3: Пусть спектральная плотность стационарного случайного процесса равна . Найти ковариационную функцию и построить функции оптимального линейного прогноза стандартным способом и с помощью вычисления условного математического ожидания.

Задание №4: 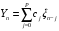, – ортонормированные случайные величины. Найти ковариационную функцию и построить функции прогноза.

Задание №5: Рекуррентный случайный процесс определяется равенством 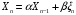, где 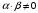, 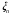– ортонормированная последовательность случайных величин, 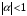. Вычислить ковариационную функцию и построить оптимальный линейный прогноз.

Выполнение работы.

Задание №1

Дано:

.

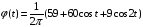Решение:

Запишем спектральную плотность в виде:

;

.

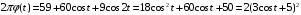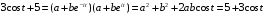Сравнивая коэффициенты, получим систему уравнений

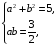
которая имеет два решения 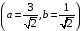и .

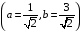Для того чтобы функция 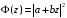не имела корней внутри единичного круга, следует выбрать решение системы 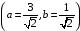, поэтому

, , , , , .

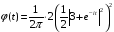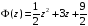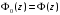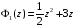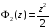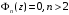Следовательно,

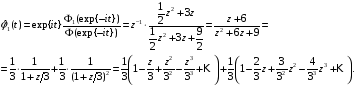
Таким образом, прогноз 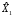имеет вид

.

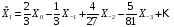Прогноз :

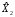Таким образом,

.

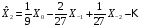Задание №2

Дано:

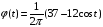
Решение: Корреляционная функция K(n) имеет вид:

;

.

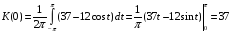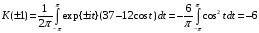Таким образом,

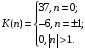
Запишем спектральную плотность в виде

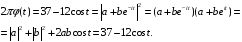
Сравнивая коэффициенты, получим систему уравнений

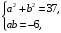
которая имеет два решения (a = 6, b = –1) и (a = 1, b = –6).

Для того чтобы функция 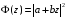не имела корней внутри единичного круга, следует выбрать решение системы (a = 6, b = –1), поэтому

, , , .

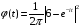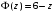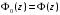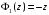Следовательно,

, , .

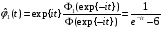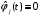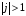Необходимо представить 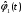в виде ряда:

.

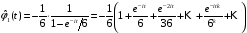Таким образом,

.

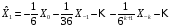Задание №3

Дано:

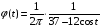
Решение: Используя спектральное представление для ковариационной функции, получим

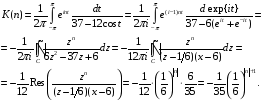
В спектре присутствуют все кратные частоты, поэтому все коэффициенты функции прогноза отличны от нуля. Корреляционная функция быстро убывает, поэтому следует ожидать прогноз, быстро сходящийся к нулю. Необходимо вычислить коэффициенты функции прогноза. Для этого необходимо записать знаменатель спектральной плотности в виде 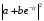. Это приведет к равенствам

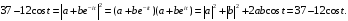
Сравнивая коэффициенты, получим систему уравнений

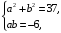
которая имеет два решения (a = 6, b = –1) и (a = 1, b = –6).

Для того чтобы функция 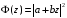не имела корней внутри единичного круга, следует выбрать решение системы (a = 6, b = –1), поэтому

,

,

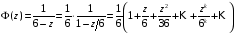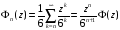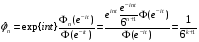
Из последнего равенства следует, что функция прогноза через n моментов времени равна .

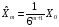Необходимо построить функции оптимального линейного прогноза с помощью вычисления условного математического ожидания:

.

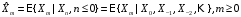В силу того, что данный процесс является непрерывным марковским, то достаточно рассмотреть 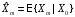. Для векторов, имеющих невырожденное совместное нормальное распределение, условное математическое ожидание является линейной функцией относительно переменной X₀, ее можно выразить через векторы математических ожиданий и ковариационные функции случайных векторов и X_m и X₀:

.

,

.

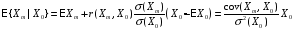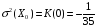Таким образом,

.

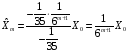Задание №4

Дано:

; ; ; ;

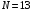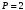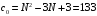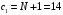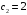
Решение:

.

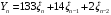Ковариационная матрица имеет вид:

Таким образом,

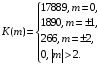
Пусть Y₀ = 0.

,

, , , .

.

;

.

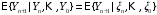
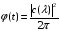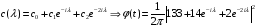
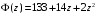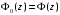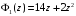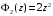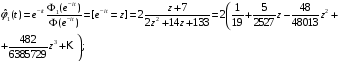
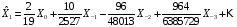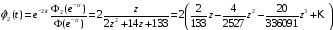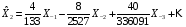Задание №5

Дано:

; ;

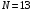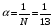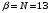
Решение:

Ковариационная норма для рекуррентного случайного процесса имеет вид:

Поскольку, 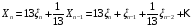, получим:

.

.

.

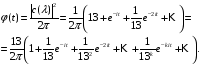
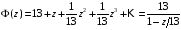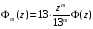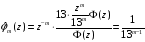
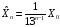Выводы.

В ходе выполнения лабораторной работы были получены навыки решения задач экстраполяции стационарных случайных процессов с дискретным временем.