Семестровая работа

Дано:

Компоненты тензора напряжений

σ_x = 80 МПа; σ_y = 70 МПа; σ_z = -60 МПа;

τ_xy = -30 МПА; τ_xz = 0; τ_yz = 0 МПа.

Определить:

1. Аналитическая часть:

1. написать кубическое уравнение, определить главные нормальные напряжения;

2. определить направляющие косинусы;

3. определить взаимное расположение главных и заданных случайных осей (x,y,z).

2. Графическая часть:

1. по найденным главным напряжениям построить круги мора;

2. с помощью кругов мора определить значение нормального σ_n и касательного τ_n напряжений на площадке с направляющими косинуса a₁ = 0,5; a₂=0,707; a₃=0,5.

Решение:

Составим матрицу тензора напряжений

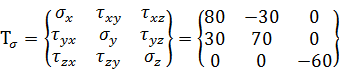, Мпа (1)

Нарисуем элементарный объем – картина напряжений

Очевидно, что на площадке z τ = 0 МПа. Значит, эта площадка является главной, а действующее на ней напряжение является одним из тройки главных нормальных напряжений. Примем что одно из главных σ’=. Это один из трех главных корней кубического уравнения:

МПа (2)

(3)

(4)

Получаем кубическое уравнение в числовом виде:

= 0

Поскольку одно из главных напряжений направлено по оси z, очевидно что 2 других расположены в плоскостях x, y, т.е. можно найти их решая плоскую задачу теории плоского напряженного состояния в плоскости xy.

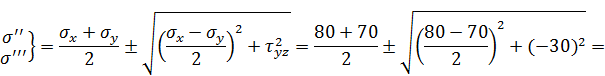
МПа

;

;

Таким образом, учитывая неравенство :

, Мпа

Поверки:

1) 90 МПа

2) МПа²

Совпадает 4275 ≈4300МПа²;

Погрешность составляет = 0,58%

3) МПа³

Совпадает – 282000 = - 282000МПа³.

Таким образом, 3 проведенные проверки показали, что корни кубического уравнения вычислены правильно. При этом ось «3» совпадает с осью z случайной системой координат, а оси «1» и «2» расположены в плоскости xy (но как пока не известно).

Что бы установить их расположение проделываем следующий анализ, т.е. определим направляющие косинусы «2» и «1» главных осей:

Для площадки 1

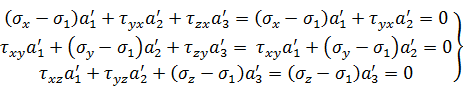(6)

Для площадки 2

(7)

Из уравнений [(6) и (7)] очевидно, что = 0, потому что []

Вывод: Если =0, следовательно, cosα₃=0 и значит α₁= 90ᵒ. Ось «3» совпадает с осью z, а значит является нормалью к плоскости xy.

Этот вывод совпадает с ранее принятым утверждением, что , т.е. фактически является дополнительной проверкой правильности определения . Таким образом, эта проверка дает окончательный ответ, какое это главное напряжение из 3ки чисел. Т.е. является окончательной проверкой.

Решаем первые 2 уравнения из группы (6), (7) используя условие , в нашем случае:

(*)

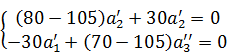
Выражаем и подставляем в (*)

→ (**)

Таким образом, угол между осями «x» и «1» α₁ = arccos= 85ᵒ

Определим направляющий косинус между «y» и осью «3»

Проверка 1

Таким образом, 1 проверка удовлетворяется.

Тогда угол между осями «x» и «2» α₂ = arccos= 0ᵒ

Проверка 2

α₂^’+ α₁^’= 85 + 0 = 84ᵒ,

погрешность составляет , что допустимо при технических расчетах.

Из группы формул (7) получаем:

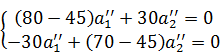
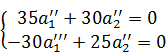
подставим в уравнение (*) → → →

Таким образом, угол между осями «y» и «1» α₁ = arccos= 85ᵒ

Определим направляющий косинус между «y» и осью «3»

Проверка 1

Таким образом, 1 проверка удовлетворяется.

Тогда угол между осями «y» и «2» α₂ = arccos= 0ᵒ

Проверка 2

α₂^’’+ α₁^’’= 85 + 0 = 84ᵒ,

погрешность составляет , что допустимо при технических расчетах.

							Лист
Изм.	Кол.уч.	Листтт	№ док.	Подп.	Дата