Laba_3

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых»

(ВлГУ)

Институт Информационных технологий и радиоэлектроники (ИИТР)

Кафедра: «Биомедицинские и электронные средства и технологии» (БЭСТ)

Лабораторная работа № 3

на тему: «Моделирование систем управления в пакете SIMULINK»

по дисциплине: «Основы управления техническими системами»

Вариант 6

Выполнил:

ст. гр. БТС-115

Лосева Е. С.

Принял:

доц. Долгов Г.Ф.

Владимир 2018

Цель работы: освоение методов моделирования линейных систем в пакете Simulink.

Задачи работы:

• научиться строить и редактировать модели систем управления в пакете Simulink

• научиться изменять параметры блоков

• научиться строить переходные процессы

• научиться оформлять результаты моделирования

• изучить метод компенсации постоянных возмущений с помощью ПИД-регулятора.

Описание системы:

В работе рассматривается система управления судном по курсу. Ее структурная схема показана на рисунке 1.

Рисунок 1 - Структурная схема системы стабилизации судна на курсе.

Линейная математическая модель, описывающая рыскание судна, имеет вид:

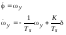
где – угол рыскания (угол отклонения от заданного курса), 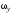– угловая скорость вращения вокруг вертикальной оси, – угол поворота вертикального руля относительно положения равновесия, 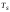– постоянная времени, – постоянный коэффициент, имеющий размерность рад/сек. Передаточная функция от угла поворота руля к углу рыскания запишется в виде: .

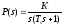Привод (рулевая машина) приближенно моделируется как интегрирующее звено, охваченное единичной отрицательной обратной связью, так что его передаточная функция равна: .

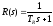Для измерения угла рыскания используется гирокомпас, математическая модель которого записывается в виде апериодического звена первого порядка с передаточной функцией .

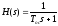Исследуются переходные процессы в системе при использовании ПД-регул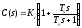ятора: , и ПИД-регулятора .

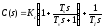Ход работы:

1. Исследование системы с ПД-регулятором.

Запускаем пакет SIMULINK, создаем новую модель с помощью File – New – Model, перетаскиваем 4 блока Transfer Fcn (передаточная функция) из окна Simulink Library Browser (группа Continuous) в окно модели и вводим числитель и знаменатель передаточной функции модели судна, привода, регулятора и гидрокомпаса с помощью команд двойным щелчком на блоке:

- Numerator [K]

- Denominator [Ts 1 0], [Tv 1 0], [T_R 1 0], [Tос 1 0] соответственно.

Подписываем блоки, сохраняем как lab3.mdl, выбираем цвета блоков с помощью ПКМ на блоке,Format – Background color. Далее добавляем блоки sum из группы Math Operations и установите его слева от регулятора, второй вход ставим на ‘-‘ с помощью двойного щелчка на блоке, вводим |+- в поле List of signs; добавляем блок Step из группы Sources и установите его слева от сумматора и подписываем Заданный курс. Устанавливаем время подачи сигнала 0 и величину сигнала 10 (исследуем поворот на 10 градусов) с помощью двойного щелчка на блоке:

0 в поле Step time

10 в поле Final value.

Затем соединяем все блоки нужным способом, также добавляем два блока Scope (осциллограф) из группы Sinks и устанавливаем их в правой части Руль и Курс.

• Передаточная функция ПД-регулятора, обеспечивающего переходный процесс минимальной длительности:

,

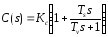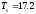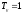где К_с = 0.712 рад/сек, сек, сек, T_R = 1 сек, Т_ос = 1 сек.

Модель системы с ПД-регулятором предст авлена на рисунке 2:

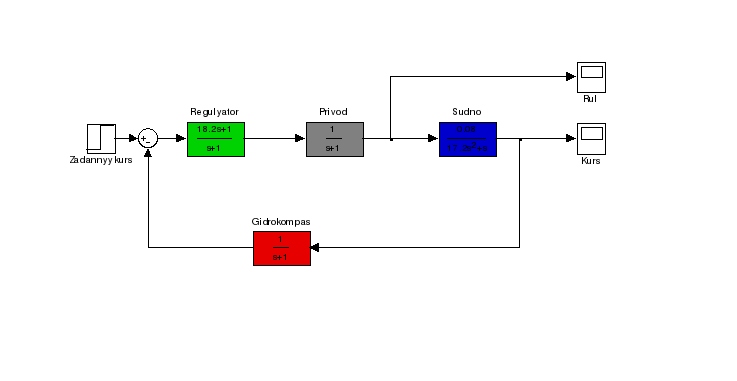
Рисунок 2 - Модель системы с ПД-регулятором.

• Устанавливаем время моделирования 100 секунд с помощью Simulation – Simulation parameters 100 в поле Stop time, выполняем моделирование, открыв окна блоков Курс и Руль, смотрим результаты моделирования, затем, чтобы результаты моделирования передавались с обоих блоков Scope в рабочую область Matlab в виде матриц, в которых первый столбец – время, а второй – сигнал (курс или угол поворота руля) необходимо выполнить: вкладка Data history

Variable name:

phi (Курс) или

delta (Руль)

Format: Array

Снова выполняем моделирование, затем переходим в командное окно Matlab и создаем новое окно для графика. В одном окне будут построены две кривых на разных осях. Разбиваем окно на 2 части по вертикали и делаем активным первый график. Первое число в команде subplot означает количество ячеек с графиками по вертикали, второе – по горизонтали, третье – номер ячейки, которую надо сделать активной. Строим график изменения курса. В команде plot сначала указывают массив абсцисс, затем – массив ординат. Двоеточие означает, что используются все строки. Вводим заголовок графика. Вводим названия осей координат. Внутри апострофов для ввода греческих букв разрешается использовать команды LaTeX, Например, «\phi» означает греческую букву 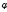, а «\delta» – букву 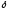. Аналогично строим во второй ячейке график изменения угла поворота руля, используя данные из массива delta, полученного в результате моделирования (см. рисунок 3).

>> figure(1);

>> subplot(2, 1, 1);

>> plot(phi(:,1),phi(:,2));

>> title('Курс');

>> xlabel('Время, сек');

>> ylabel('\phi, градусы');

>> subplot(2, 1, 2);

>> plot(delta(:,1),delta(:,2));

>> title('Угол поворота руля');

>> xlabel('Время, сек');

>> ylabel('\delta, градусы');

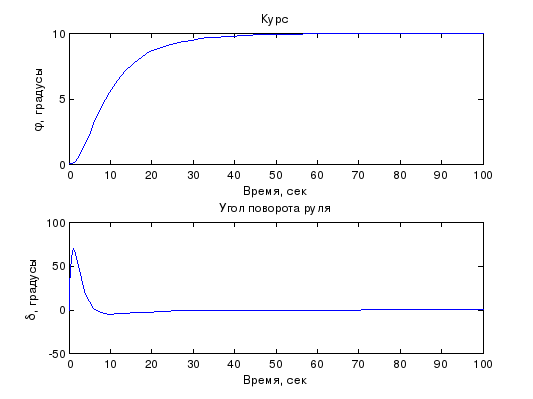
Рисунок 3 – График курса и угла поворота руля.

Удаляем в окне модели связь между приводом и объектом. Добавляем еще один блок Sum из группы Math Operations и устанавливаем его на освободившееся место. Настраиваем расположение входов и выхода так, чтобы первый вход был в верхней части круга. Двойной щелчок по блоку ++| в поле List of signs.

Исследуем реакцию системы на постоянный сигнал, приложенный непосредственно к входу объекта. Он может моделировать какое-то постоянное возмущающее воздействие, например, влияние ветра.

Копируем блок Заданный курс, перетащив его правой кнопкой мыши, и устанавливаем для него величину скачка 2 градуса и называем Возмущение. Подключаем его выход к новому сумматору. Достраиваем нужные соединительные линии. Перетаскивание ПКМ. Двойной щелчок по блоку, 2 в поле Final Value, двойной щелчок по имени

Модель системы с ПД-регулятором с учетом внешнего возмущения представлена на рисунке 4:

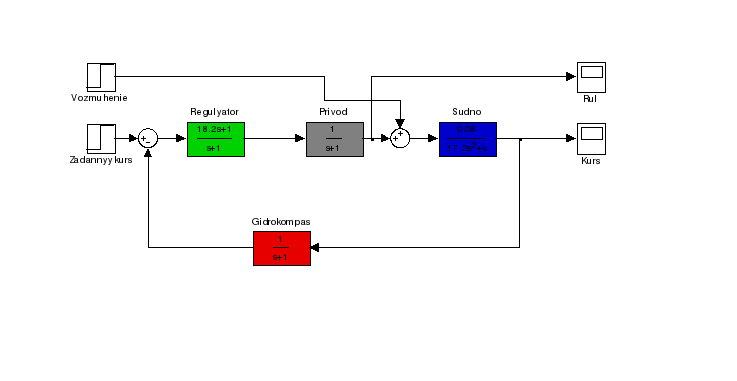
Рисунок 4 - Модель системы с ПД-регулятором с учетом внешнего возмущения.

Увеличиваем время моделирования до 500 и выполняем моделирование. Simulation – Simulation parameters - Stop time (см. рисунок 5):

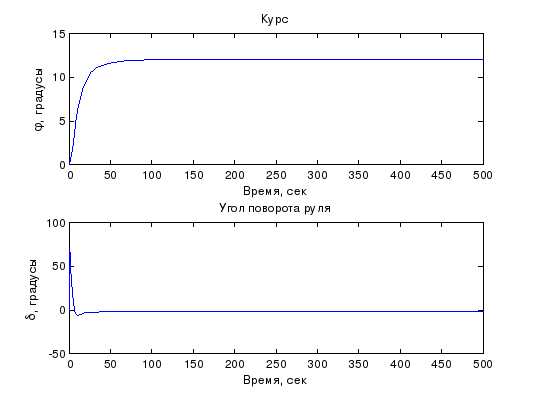
Рисунок 5 - Модель системы с ПД-регулятором с временем регулирования 500 секунд.

Строим передаточную функцию по возмущению замкнутой системы с ПД-регулятором и находим коэффициент усиления в установившемся режиме и рассчитываем установившееся значение сигнала выхода при заданном курсе 10 градусов и постоянном возмущении, эквивалентном 2 градусам поворота руля.

Передаточная функция по возмущению замкнутой системы с ПД-регулятором:

>> W = C*G / (1 + C*G*H)

W =

1.376 s^4 + 2.832 s^3 + 1.536 s^2 + 0.08 s

----------------------------------------------------------------------------

295.8 s^7 + 921.9 s^6 + 991.7 s^5 + 402 s^4 + 38.78 s^3 + 2.456 s^2 + 0.08 s

Судно с ПД-регулятором не вышло на заданный курс 10 градусов, потому что функция имеет нули в s=0.

Статический коэффициент усиления k=0.712, установившееся значение сигнала выхода должно быть равно 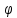=14.24, потому что постоянное возмущение, равное 2, напрямую суммируется с установившимся значением сигнала в отсутствии возмущения, равным 10; эти данные согласуются с результатами моделирования.

2. Исследование системы с ПИД-регулятором.

Добавляем интегральный канал, получается ПИД-регулятор. Подключаем параллельно регулятору интегрирующее звено с передаточной функцией 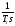, 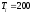сек.

Передаточная функция ПИД-регулятора:

,

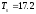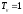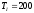где К_с = 0.08 рад/сек, сек, сек, T_R = 1 сек, Т_ос = 1 сек, сек,

Модель системы с ПИД-регулятором с учетом внешнего возмущения представлена на рисунке 6.На рисунке 7- результаты моделирования.

Рисунок 6 - Модель системы с ПИД-регулятором с учетом внешнего возмущения.

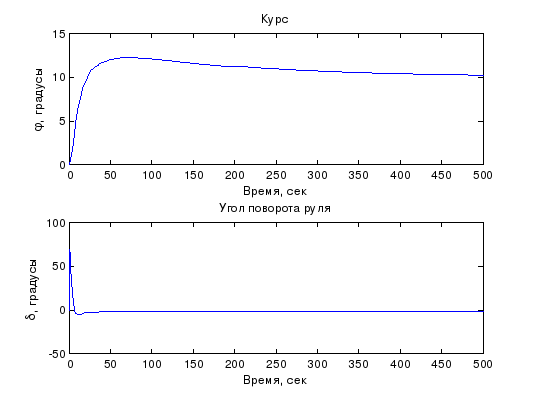
Рисунок 7 - Модель системы с ПИД-регулятором с учетом внешнего возмущения (результаты моделирования).

Передаточная функция по возмущению для системы с ПИД-регулятором:

>> W = C*G / (1 + C*G*H) передаточная функция

W =

295.8 s^7 + 921.9 s^6 + 1267 s^5 + 968.4 s^4 + 346 s^3 + 18.46 s^2 + 0.08 s

-----------------------------------------------------------------------------------

5.917e004 s^8 + 184384 s^7 + 198344 s^6 + 80408 s^5 + 7755 s^4 + 491.2 s^3 + 16 s^2

При использовании ПИД-регулятора судно выходит на заданный курс, потому что благодаря входящему в систему интегратору передаточная функция по возмущению принимает значение 0 при постоянном возмущении.

Статический коэффициент усиления k_s=0.0125, установившееся значение сигнала выхода должно быть равно =10; эти данные согласуются с результатами моделирования.

Переходные процессы в системах с ПД- и ПИД-регуляторами (см.рисунок 8):

Рисунок 8 – Переходные процессы в системах с ПД- и ПИД-регуляторами.

При использовании ПИД-регулятора вместо ПД-регулятора судно выходит на курс вне зависимости от внешнего возмущения, при этом сигнал управления практически не изменился. Но в то же время, при использовании ПИД-регулятора, в первые минуты происходит значительное отклонение от курса (перерегулирование возросло).

Передаточная функция разомкнутой системы с ПИД-регулятором:

0.08

----------------------------------

17.2 s^4 + 35.4 s^3 + 19.2 s^2 + s

Запасы устойчивости: по амплитуде gm =15.2 дБ, по фазе =55.3 градуса, запасы являются достаточными.

Вывод: в результате выполнения лабораторной работы освоены методы моделирования линейных систем в пакете Simulink.