Свойства реальных смесей

Ранние было уже рассмотрена свойство смеси идеальных газов которая выглядит так.

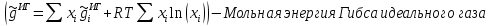
Сейчас будет рассматриваться свойства идеальной смеси, которая выглядит так. Которая отличается от идеального газа в том, что параметры подставляются реальных веществ.

Не смотря на это это тоже модель идеальная для того чтобы понять рассмотрим следующий пример, имеется система объемом V в этой системы находится 2 газа которые разделены перегородкой. Рассмотрим, когда этой перегородки нету, тогда объем системы выглядит так.

Странное явление, не так ли. В системе из 2 объемов системы неожиданно появился 3, который называю избыточным объемом. Природа этого объема в том что появилась некоторое новая взаимодействия между частицами, которого раньше не было, дела в том что она быть и положительной, так и отрицательной, также и нулевым.

Если делать все кратко получается отличие между реальных смесей от идеальных в том что появляется избыточное свойства.

Рассмотрим случай когда газ умеренно плотный, в этом случаи можно использовать Вириальное приближение. Справедливо следующая выражение для чистого вещества.

Как было сказано ранее, имеется смесь компонентов, которая имеет свои потенциалы взаимодействие тогда, тогда 2 вириальный коэффициент можно определить как.

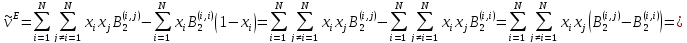
Зная данное выражение, определим некоторые избыточные функции

Данный способ является не единственный в определении избыточных функций, например можно обратиться к парциальным функциям.

Так как концентрация является входным параметром, то по уравнению Гиббса-Дюгема

Если предположить что нам известна функция (), то из нее можно определить неизвестные элементы.

Обратимся к примеру

Фугитивность можно определить следующим образом для смеси идеальной смеси, которая равна произведению мольной концентрации на фугитивность чистого компонента. Если рассматривать реальную смесь то данное выражение нужно до множить на активность компонента.

Фазовое равновесия много компонентной смеси

Рассмотрим самый простой случай однокомпонентной смеси. Максимальное количество контакта фаз будет 3 и находится она в тройной точке. При таком контакте выполняется основные тождества температуры фаз одинаковые, давление одинаковая и химический потенциал (энергия Гиббса).

По сути дела в многокомпонентной смеси происходят теже самые элементы и весь свой анализ будет строиться из того что равновесное состояние соответствует минимуму энергии Гиббса.

Было предположено, что

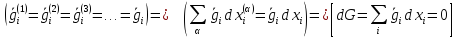
Определим степени свободы (независимых переменных). Очевидно, что 2 из них это P,V , концентрации каждой фазы каждого вещества. С другой стороны имеется связь между концентрациями в одной фазе, которых А штук, и связь между энергиями Гиббса, которых А-1 для N веществ

Выпишем все известные величины, которые касаются смеси компонентов

Используя эти выражение можно получить следующее тождества

Рассмотрим систему из 2 компонентов находящийся в 2 фазах. По правилу фаз Гиббса, количество не зависимых элементов будет 2.