8 Семестр

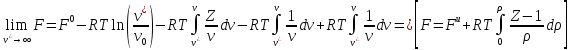
В этом месте объясняется, как найти статистическую сумму реального вещества. Раньше предполагалось, что потенциальной энергии системы нету.

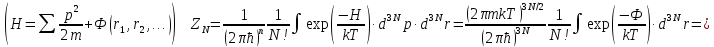
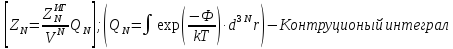
Для определения данного интеграла, что такая потенциальная энергия это сумма попарных взаимодействий системы, да такое решение не самое лучшее, но по лучше ничего не придумали.

Далее определим (m_i-количество I частичных групп) с помощью которых можно определить групповые функции (S). Тогда (W_N) можно определить как сумму вкладов всех возможных прономерованных разбиений групп. Например.

Даже не смотря на упрощение задачи определить от суда контурный интеграл получится, но слишком сложно. Поэтому будем определять большую статистическую сумму.

При использование такого метода вириальные коэффициенты определяются следующим образом

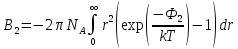
По достаточно очевидным причинам на электрические заряды действует силы, такие как электрические гравитационные. Так как гравитационные силы намного меньше, чем электрические, то принципе их можно не учитывать по сравнению с электрическими. Далее рассмотрим, как определить потенциальную энергию электрических зарядов дальнейшем будет показана, что она определяется действиями электрическим моментами.

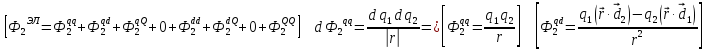
Далее, как известно действие электрического поля на атом приводит к изменению электрического поля атома, из-за чего возникает дополнительный индукционный дипольный момент, который добавляет свою часть в потенциальной энергии.

Независимо от наличии у молекулы, каких то моментов, она все равно как то взаимодействует с другой молекулой, такое взаимодействие называют дисперсионной взаимодействием. Это взаимодействие обусловлена электрическими силами, электроны как легкие частицы отклоняются от своей нормальной радиуса, из-за чего и возникает дополнительный момент. Когда частицы находятся на большом расстоянии такое взаимодействие обусловлено притяжением их друг другу. Когда частицы приблизились достаточно друг другу, начинают провялятся квантовые эффекты частиц что приводит к появлению силы отталкивание друг от друга.

Вещество	H	He	Ne	Ar	Kr	Li	Na	Rb	F	Cl	Br
	4.5	1.37	2.67	11.09	16.72	162	162	269	3.76	15	26
	6.2	1.46	6.88	66.9	135	-	1600	3800	-	-	-

Потенциалы Ленардо-Джонса и Букиннгема – это такие потенциалы, которые описывает слабое взаимодействие частиц или слабое Ван-дер-Ваальса взаимодействие.

Следующие потенциалы для молекулярного взаимодействие (образование молекулы и фазовые переходы)

Если взять потенциал Ленардо – Джонса и безразмерить его, то данная потенциал будет универсальным для любого вещества. Если с помощи его определять вириальные коэффициенты, то они выглядят следующим образом.

Казалось бы все хорошо универсальный потенциал для любого вещества, можно определить поправку на не идеальность, но это не так. При малых температурах вириальные коэффициенты определяются не правильно, так как начинаю проявляться квантовые эффекты частиц, из-за чего универсальность теряется. Приходится водить некоторую поправку на квантовость в которая входит число Де Бура, в которой входят уникальные параметры вещества.

Если усложнить модель и взять другой потенциал проблема возникнет примерно такая же, возникнет элемент в безразмерном виде включающие уникальные параметры вещества.